WGAN-GP学习笔记(从理论到Pytorch实践)
WGAN相关学习,主要文献 improved of training of WGAN
首先我们需要明白一般的GAN数学表达式如下:
m a t h m i n G m a x D E x ∼ P r [ l o g ( D ( x ) ) ] + E x ~ ∼ P g [ l o g ( 1 − D ( x ~ ) ) ] math \mathop{min}\limits_{G}\mathop{max}\limits_{D}\mathop{E}\limits_{x\sim{P_r}}[log(D(x))] + \mathop{E}\limits_{\widetilde{x}\sim{P_g}}[log(1-D(\widetilde{x}))] mathGminDmaxx∼PrE[log(D(x))]+x ∼PgE[log(1−D(x ))]
这里 P r P_r Pr表示的是真实数据的分布, P g P_g Pg是由模型产生出来的产生出来的分布,而此时模型产生出的分布,根据GAN的原始论文记载是输入到generator中的‘噪声’,从原始论文来看,如果discriminator在generator的参数进行更新之前进行优化,上述式子求最小值的过程可以等效为求上述 P r P_r Pr和 P g P_g Pg之间的JS散度距离,但是这样做很容易导致discriminator饱和,即用于更新discriminator参数的反向传播梯度消失
针对上述问题,提出了WGAN来解决
WGAN
WGAN的原始论文中提到generator在训练过程中,当发生偏离最优解时,这时有可能导致generator的参数的更新不联续,这带来了generator训练的困难,这时WGAN的作者提出改造上述GAN的优化公式方法来解决问题,他们提出使用Wasserstein-1距离作为网络训练的优化目标,作者基于Kantorovich-Rubinstein对偶性推导,改造上述的传统GAN公式:
m i n D m a x D ∈ D E x ∼ P r [ D ( x ) ] − E x ~ ∼ P g [ D ( x ~ ) ] \mathop{min}\limits_{D}\mathop{max}\limits_{D\in{D}}\mathop{E}\limits_{x\sim{P_r}}[D(x)] - \mathop{E}\limits_{\widetilde{x}\sim{P_g}}[D(\widetilde{x})] DminD∈Dmaxx∼PrE[D(x)]−x ∼PgE[D(x )]
在这里D是1-Lipschitz函数集, P g P_g Pg同上述
尽管WGAN在训练上比普通的GAN更为容易,但是WGAN仍然是有一些局限的,这些局限来源于在传统的WGAN中为了确保Lipschitz约束
WGAN中确保Lipschitz连续性带来的问题
实际上在WGAN提出后不久,很多人发现WGAN的训练存在着收敛速度慢等问题,improved Training of Wasserstein GANs这篇文章中就分析到,认为是WGAN变化推导过程中的Lipschitz限制的处理是主要原因,Lipschitz限制具体表现为判别器D(x)梯度不大于一个有限的常数
∣ ∣ ▽ D ( x ) ∣ ∣ P ≤ K , ∀ x ∈ R ||\bigtriangledown{D(x)}||_P \leq{K},\forall{x}\in{R} ∣∣▽D(x)∣∣P≤K,∀x∈R
对这里直观上的理解,就是指输入样本略微发生变化时,导致的判别器计算出的值不能发生跃变,那么这一点主要是通过限制Dscriminator中的权重变化来实现的,就是weight clipping来实现的,从代码上来操作就是在每一次更新完discriminator的权重后,就检查一遍里面的权重有没有超过一个阈值,比如0.01,有的话,就把这些参数修饰到[-0.01,0.01]范围内;这个也比较好理解,因为输入样本变化很小,那么理应discriminator的权重变化很小,这样导致计算出的结果是变换很小的,如果权重变化很大,那么很显然有可能导致一个变化很大的discriminator输出。
weight clipping存在的问题
第一个问题: 在WGAN的loss 中,如果是任由weight clipping去独立的限制网络参数的取值范围,有一种可能是大多数网络权重参数会集中在最大值和最小值附近而并不是一个比较好的连续分布,论文的作者通过实验也确实发现是这样一种情况。这毫无疑问带来的结果就是使得discriminator更倾向于拟合一种简单的描述函数,这种函数的泛化能力以及判断能力毫无疑问是非常弱的,那么经过这种discriminator回传的梯度信息的质量也是很差的
第二个问题: weight clipping的处理很容易导致梯度消失或者梯度爆炸,因为discriminator虽然相对于generator来说结构较为简单,但其实也是一个多层结构,如果weight clipping的约束比较小的话,那么经过每一层网络,梯度都会变小,多层之后的情况就类似于一个指数衰减了,这样得到的结果就会导致梯度消失,反之则是梯度爆炸,这实际上weight clipping的设置就非常的微妙了。下图是论文作者实验所得结果,确实可以观察到在未使用gradient penalty之前,权重集中于clipping的两端

下图是论文作者针对梯度爆炸和梯度消失所做的实验结果
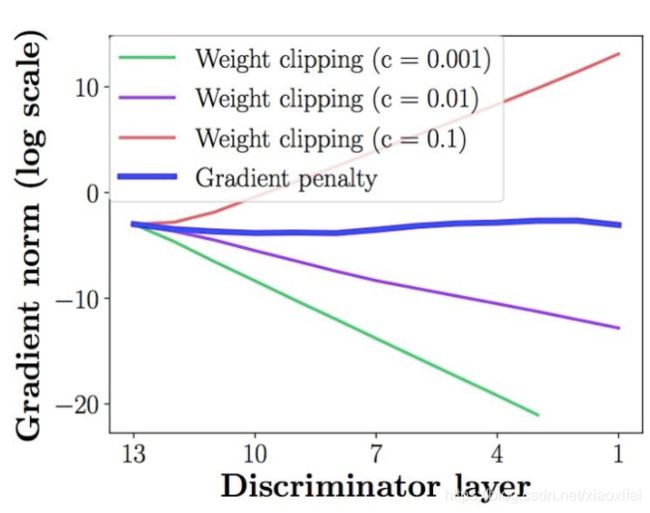
由上面的两张图,就直观了解到clipping的问题。
针对weight clipping的解决方法
论文中提出使用gradient penalty的方式来进行自适应的权重修正。
思想来源是这样的:既然discriminator的作用是尽量判别出真假样本的分数差距,那么对于 ▽ D ( x ) \bigtriangledown{D(x)} ▽D(x),应该是越大越好,出于这样的理解,比较优秀的discriminator的梯度,考察最初的公式,应该是在K值附近,这里作者提出了使用如下欧氏距离的方式来衡量这种接近程度
[ ∣ ∣ ▽ D ( x ) ∣ ∣ − K ] 2 [||\bigtriangledown_{D(x)}|| - K]^2 [∣∣▽D(x)∣∣−K]2
假定这里的k就是1,在跟原来WGAN的discriminator 目标函数表达式结合
− E x ∼ P r [ D ( x ) ] + E x ∼ P g [ D ( x ) ] + λ E x ∼ χ [ ∣ ∣ ▽ x D ( x ) ∣ ∣ − 1 ] 2 -E_{x\sim{P_r}}[D(x)] + E_{x\sim{P_g}}[D(x)] +\lambda E_{x\sim_{\chi}}[||\bigtriangledown_{x}{D(x)}|| -1]^2 −Ex∼Pr[D(x)]+Ex∼Pg[D(x)]+λEx∼χ[∣∣▽xD(x)∣∣−1]2
但是在这里还是有问题的,因为这个表达式的最后一项描述的是需要在整个样本空间进行采样,这个肯定是不行的,论文中针对这个问题指出,只需要在generator生成样本和真实样本空间以及之间的区域就可以了,作者使用如下方法:首先随机取出一对真假样本,还有一个0~1均匀分布的随机数
x r ∼ P r , x g ∼ P g , ϵ ∼ U n i f o r m [ 0 , 1 ] x_r\sim{P_r} \text{ } ,x_g \sim{P_g} \text{ },\epsilon \sim{Uniform[0,1]} xr∼Pr ,xg∼Pg ,ϵ∼Uniform[0,1]
再然后在 x r x_r xr和 x g x_g xg之间的连线上随机采样
x ∼ = ϵ x r + ( 1 − ϵ ) x g \mathop{x}\limits^{\sim} = \epsilon x_r +(1- \epsilon)x_g x∼=ϵxr+(1−ϵ)xg
将这样采样的结果所满足的分布记为 P x ∼ P_{\mathop{x}\limits^{\sim}} Px∼,则此时可以对discriminator的loss改造为
L ( D ) = − E x ∼ P r [ D ( x ) ] + E x ∼ P g [ D ( x ) ] + λ E x ∼ P x ∼ [ ∣ ∣ ▽ D ( x ) ∣ ∣ − 1 ] 2 L(D) = -E_{x\sim{P_r}}[D(x)] + E_{x\sim{P_g}}[D(x)]+\lambda E_{x\sim{P_{\mathop{x}\limits^{\sim}}}}[||\bigtriangledown D(x)||-1]^2 L(D)=−Ex∼Pr[D(x)]+Ex∼Pg[D(x)]+λEx∼Px∼[∣∣▽D(x)∣∣−1]2
到了这一步其实还有一个问题就是实际上梯度上回传的时候,由于最后一项的出现会产生一个梯度的梯度,但是在这里面pytorch实际上也可以处理;虽然没有直接使用过tensorflow,但是据人说应该也是可以满足最后一项的
WGAN-GP论文中提到的注意事项
- 根据论文的描述,上述discriminator目标函数中的 λ \lambda λ推荐取10,作者在很多模型以及数据集上进行测试,推荐该数值较为合适
- discriminator的结构中不引入batch normalization,因为这会引入通过batch中不同样本的依赖关系,论文经过测试推荐使用layer normalization
- 论文推荐最好将梯度归一化到1,也就是做一个归一化过程,这被论文称之为two-sided penalty,作者指出这样做会有一定的提高
Pytorch WGAN-GP的实现
实现代码示例如下,相对于WGAN的情况WGAN-GP主要是将原有的discriminator 的权重clipping修改为gradient penalty:
# gradient penalty
alpha = torch.rand((self.batch_size, 1, 1, 1))
if self.gpu_mode:
alpha = alpha.cuda()
x_hat = alpha * x_.data + (1 - alpha) * G_.data
x_hat.requires_grad = True
pred_hat = self.D(x_hat)
if self.gpu_mode:
gradients = grad(outputs=pred_hat, inputs=x_hat, grad_outputs=torch.ones(pred_hat.size()).cuda(),
create_graph=True, retain_graph=True, only_inputs=True)[0]
else:
gradients = grad(outputs=pred_hat, inputs=x_hat, grad_outputs=torch.ones(pred_hat.size()),
create_graph=True, retain_graph=True, only_inputs=True)[0]
gradient_penalty = self.lambda_ * ((gradients.view(gradients.size()[0], -1).norm(2, 1) - 1) ** 2).mean()
D_loss = D_real_loss + D_fake_loss + gradient_penalty
D_loss.backward()
self.D_optimizer.step()
参考资料
[1]. Ishaan Gulrajani. Improved training of Wasserstein GANs
[2]. https://www.zhihu.com/question/52602529/answer/158727900
[3]. https://arxiv.org/abs/1606.03657
[4]. https://github.com/igul222/improved_wgan_training
[5]. https://github.com/tjwei/GANotebooks