SVM深入理解&人脸特征提取
目录
- 一.SVM深入理解
-
- 1.支持向量机(SVM)
- 2.惩罚参数C
- 3.核函数
- 4.多分类支持向量机
- .5.鸢尾花数据集
-
- 5.1线性处理
- 5.2 多项式分类
- 5.3高斯核
- 6.月亮数据集
-
- 6.1线性SVM
- 6.2多项式核
- 6.3高斯核
- 二.人脸特征提取
-
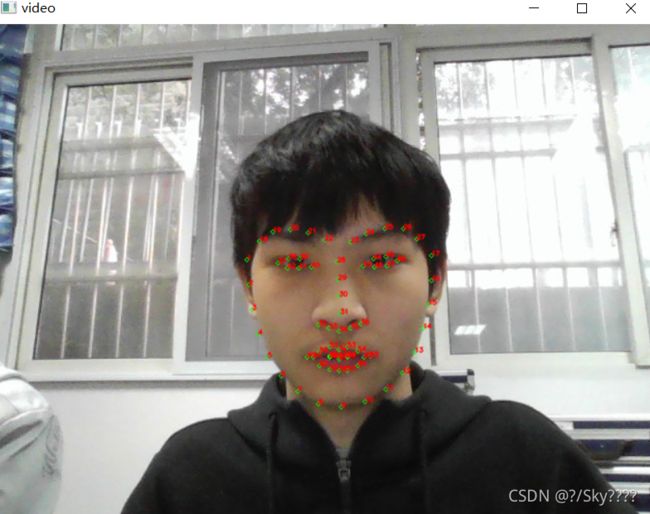
- 1.用python3+opencv3.4+dlib库编程,打开摄像头,实时采集人脸并保存、绘制68个特征点
- 2.给人脸虚拟P上一付墨镜
- 总结
- 参考
一.SVM深入理解
1.支持向量机(SVM)
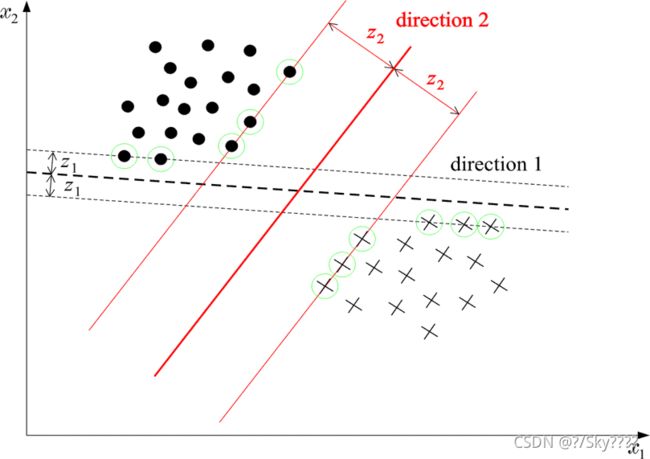
给定训练样本集,在特征空间上找到一个分离超平面,将样本点分到不同的类。其中当且存在唯一的分类超平面,使得样本点距离分类超平面的距离最大。其中,距离超平面最近的点为该超平面的支持向量。
找到超平面后,对于待测点,通过计算该点相对于超平面的位置进行分类。其中,一个点距离分离超平面的距离越大,表示分类预测的确信程度越高。
SVM的数学推导非常繁琐,我个人了解得还不够透彻,推荐去看李航编写的《统计学习方法》,里面的数学理论推导非常详细。还有斯坦福大学的公开课《机器学习》,对这部分讲解得深入浅出,非常推荐。
2.惩罚参数C
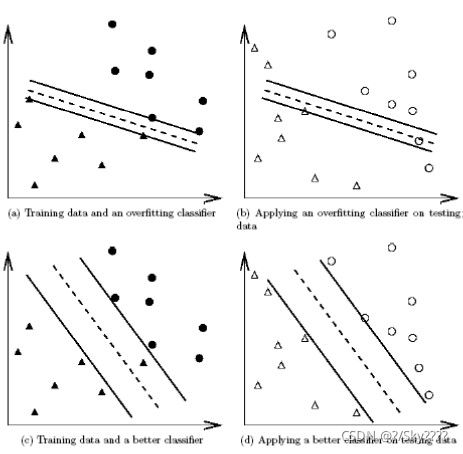
惩罚参数表示对误分类点的惩罚权重。 如下图所示,惩罚参数的设置相当与在训练集的误差和间隔平面的距离上做一个折衷选择。当惩罚参数过大,如(a)易出现过拟合的情况,预测时,易导致误分情况。减小惩罚参数,开始容忍样本点落入间隔平面之内。过小会导致训练集的样本点对结果影响变小分类功能丧失。因此,选择合适的惩罚参数,会大大提高分类器的性能,非常关键。 实际运用过程中,采用交叉验证的方法选择合适的参数C。
在这里简要的提一下交叉验证(Cross Validation)的思想:即将所有的样本分成:训练集(train set),验证集(validation set)和测试集(test set),合适的划分比例如(3:3:4),使用不同的参数训练样本,在验证集上验证表现性能,得到一组最佳参数再应用在测试集上计算最终精度。此方法可大大减少因设置参数花费的时间。
3.核函数
实际的训练集通常是线性不可分的,这就需要运用到核技巧将原空间中的点映射到线性可分的高维空间。
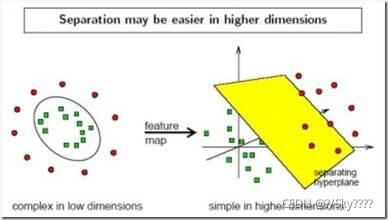
常用的核函数有:线性核函数、多项式核函数、高斯核函数(RBF核函数),sigmoid核函数。
核函数的选择对分类器的影响较大。
4.多分类支持向量机
实际分类通常涉及多类问题的区分,而SVM的理论是二类问题的区分,解决多类问题通常的方法如下,前两种方法最常见:
- 一对多(one-vs-rest)
构造k个SVM,分类时将未知样本分类为具有最大分类值的那类。 - 一对一(one-vs-one)
任意两个样本之间设计一个SVM共n(n-1)/2,分类时为得票最多的类。 - 层次分类(H-SVMs)
分层:所有类别分成子类,子类再分,循环得到单独的类。
.5.鸢尾花数据集
引包与绘制
import numpy as np
from sklearn import datasets #导入数据集
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from matplotlib.colors import ListedColormap
# 边界绘制函数
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
# meshgrid函数是从坐标向量中返回坐标矩阵
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new)#获取预测值
zz=y_predict.reshape(x0.shape)
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D'])
plt.contourf(x0,x1,zz,cmap=custom_cmap)
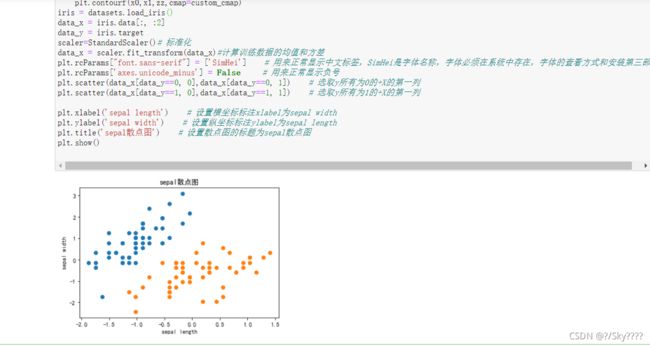
iris = datasets.load_iris()
data_x = iris.data[:, :2]
data_y = iris.target
scaler=StandardScaler()# 标准化
data_x = scaler.fit_transform(data_x)#计算训练数据的均值和方差
plt.rcParams["font.sans-serif"] = ['SimHei'] # 用来正常显示中文标签,SimHei是字体名称,字体必须在系统中存在,字体的查看方式和安装第三部分
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.scatter(data_x[data_y==0, 0],data_x[data_y==0, 1]) # 选取y所有为0的+X的第一列
plt.scatter(data_x[data_y==1, 0],data_x[data_y==1, 1]) # 选取y所有为1的+X的第一列
plt.xlabel('sepal length') # 设置横坐标标注xlabel为sepal width
plt.ylabel('sepal width') # 设置纵坐标标注ylabel为sepal length
plt.title('sepal散点图') # 设置散点图的标题为sepal散点图
plt.show()
5.1线性处理
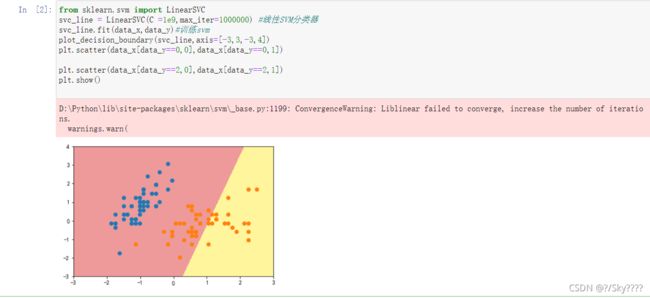
from sklearn.svm import LinearSVC
svc_line = LinearSVC(C =1e9,max_iter=1000000) #线性SVM分类器
svc_line.fit(data_x,data_y)#训练svm
plot_decision_boundary(svc_line,axis=[-3,3,-3,4])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==2,0],data_x[data_y==2,1])
plt.show()
5.2 多项式分类
from sklearn.preprocessing import PolynomialFeatures #导入多项式回归
from sklearn.pipeline import Pipeline #导入python里的管道
def PolynomialSVC(degree,c=5):#多项式svm
"""
:param d:阶数
:param C:正则化常数
:return:一个Pipeline实例
"""
return Pipeline([
# 将源数据 映射到 3阶多项式
("poly_features", PolynomialFeatures(degree=degree)),
# 标准化
("scaler", StandardScaler()),
# SVC线性分类器
("svm_clf", LinearSVC(C=c, loss="hinge", random_state=10,max_iter=100000))
])
poly_svc=PolynomialSVC(degree=5)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[-3,4,-4,5])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==2,0],data_x[data_y==2,1])
plt.show()
5.3高斯核
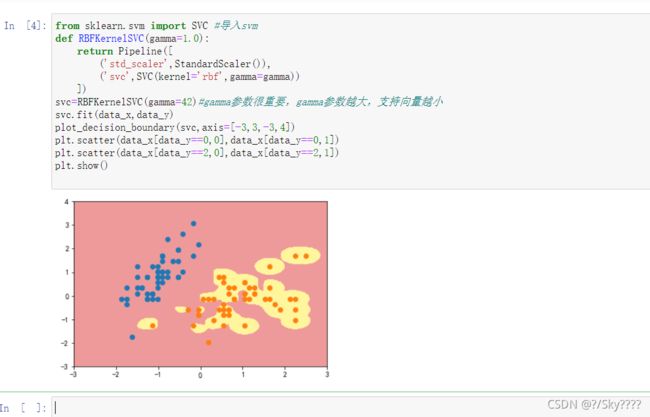
from sklearn.svm import SVC #导入svm
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
svc=RBFKernelSVC(gamma=42)#gamma参数很重要,gamma参数越大,支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-3,3,-3,4])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==2,0],data_x[data_y==2,1])
plt.show()
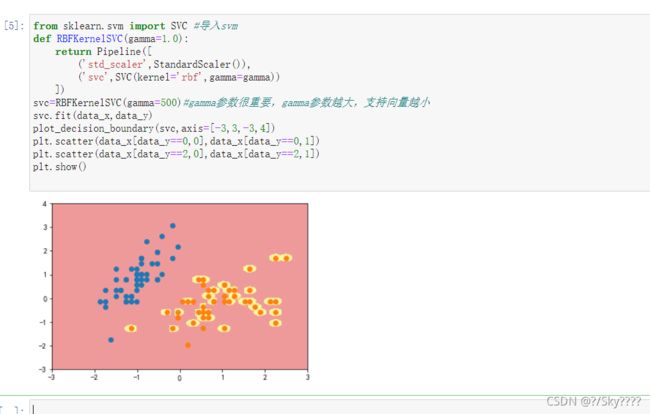
from sklearn.svm import SVC #导入svm
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
svc=RBFKernelSVC(gamma=500)#gamma参数很重要,gamma参数越大,支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-3,3,-3,4])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==2,0],data_x[data_y==2,1])
plt.show()
gamma取值越大,就是高斯分布的钟形图越窄,这里相当于每个样本点都形成了钟形图。很明显这样是过拟合的
6.月亮数据集
6.1线性SVM
# 导入月亮数据集和svm方法
#这是线性svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()# 标准化
scaler.fit(data_x)#计算训练数据的均值和方差
data_x=scaler.transform(data_x) #再用scaler中的均值和方差来转换X,使X标准化
liner_svc=LinearSVC(C=1e9,max_iter=100000)#线性svm分类器,iter是迭达次数,c值决定的是容错,c越大,容错越小
liner_svc.fit(data_x,data_y)
# 边界绘制函数
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
# meshgrid函数是从坐标向量中返回坐标矩阵
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new)#获取预测值
zz=y_predict.reshape(x0.shape)
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,zz,cmap=custom_cmap)
#画图并显示参数和截距
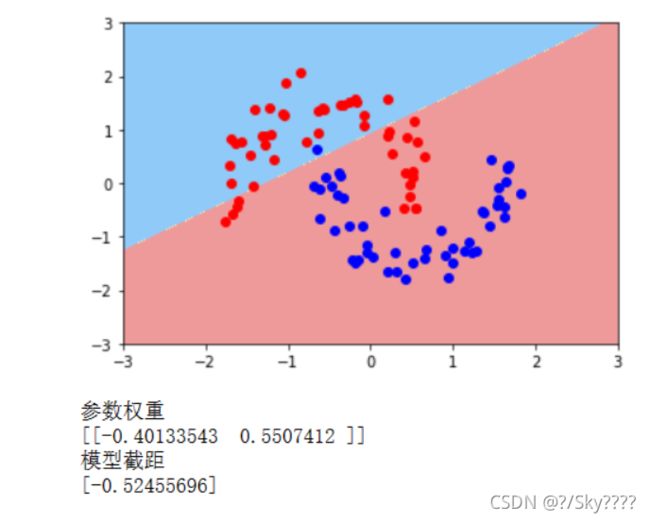
plot_decision_boundary(liner_svc,axis=[-3,3,-3,3])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(liner_svc.coef_)
print('模型截距')
print(liner_svc.intercept_)
6.2多项式核
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
X, y = datasets.make_moons() #使用生成的数据
#print(X.shape) # (100,2)
#print(y.shape) # (100,)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

生成噪声点
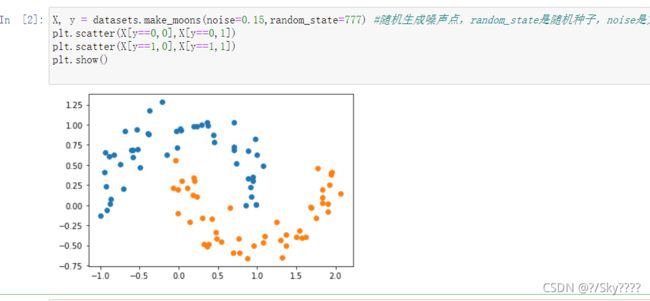
定义非线性SVM函数,调用PolynomialSVC函数进行分类可视化,进行核处理
def PolynomialSVC(degree,C=1.0):
return Pipeline([
("poly",PolynomialFeatures(degree=degree)),#生成多项式
("std_scaler",StandardScaler()),#标准化
("linearSVC",LinearSVC(C=C))#最后生成svm
])
poly_svc = PolynomialSVC(degree=5)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
def PolynomialKernelSVC(degree,C=1.0):
return Pipeline([
("std_scaler",StandardScaler()),
("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
])
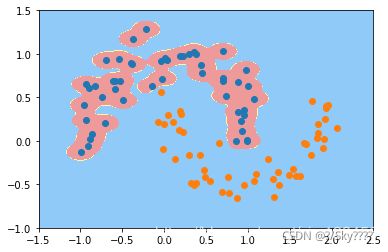
poly_kernel_svc = PolynomialKernelSVC(degree=5)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
6.3高斯核
导入包与可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
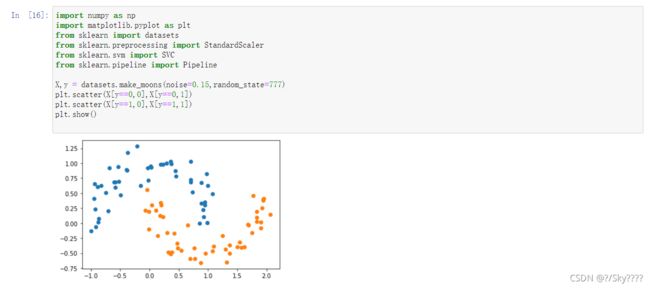
X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
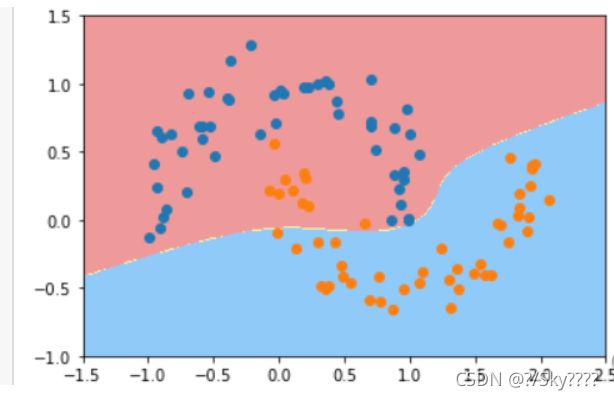
svc = RBFKernelSVC(gamma=200)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
二.人脸特征提取
1.用python3+opencv3.4+dlib库编程,打开摄像头,实时采集人脸并保存、绘制68个特征点
import numpy as np
import cv2
import dlib
import os
import sys
import random
# 存储位置
output_dir = 'C:/Users/30612/Pictures/Camera Roll'
size = 64
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# 改变图片的亮度与对比度
def relight(img, light=1, bias=0):
w = img.shape[1]
h = img.shape[0]
#image = []
for i in range(0,w):
for j in range(0,h):
for c in range(3):
tmp = int(img[j,i,c]*light + bias)
if tmp > 255:
tmp = 255
elif tmp < 0:
tmp = 0
img[j,i,c] = tmp
return img
#使用dlib自带的frontal_face_detector作为我们的特征提取器
detector = dlib.get_frontal_face_detector()
# 打开摄像头 参数为输入流,可以为摄像头或视频文件
camera = cv2.VideoCapture(0)
#camera = cv2.VideoCapture('C:/Users/CUNGU/Videos/Captures/wang.mp4')
ok = True
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor('D:/GoogleDownload/shape_predictor_68_face_landmarks.dat')
while ok:
# 读取摄像头中的图像,ok为是否读取成功的判断参数
ok, img = camera.read()
# 转换成灰度图像
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
rects = detector(img_gray, 0)
for i in range(len(rects)):
landmarks = np.matrix([[p.x, p.y] for p in predictor(img,rects[i]).parts()])
for idx, point in enumerate(landmarks):
# 68点的坐标
pos = (point[0, 0], point[0, 1])
print(idx,pos)
# 利用cv2.circle给每个特征点画一个圈,共68个
cv2.circle(img, pos, 2, color=(0, 255, 0))
# 利用cv2.putText输出1-68
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(img, str(idx+1), pos, font, 0.2, (0, 0, 255), 1,cv2.LINE_AA)
cv2.imshow('video', img)
k = cv2.waitKey(1)
if k == 27: # press 'ESC' to quit
break
camera.release()
cv2.destroyAllWindows()
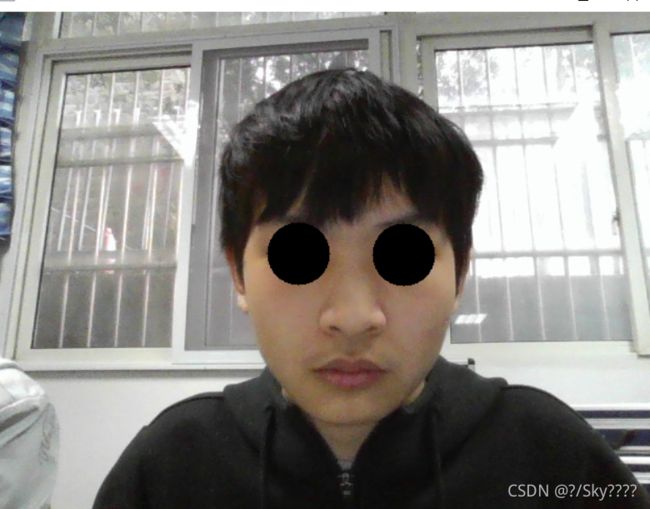
2.给人脸虚拟P上一付墨镜
import numpy as np
import cv2
import dlib
import os
import sys
import random
def get_detector_and_predicyor():
#使用dlib自带的frontal_face_detector作为我们的特征提取器
detector = dlib.get_frontal_face_detector()
"""
功能:人脸检测画框
参数:PythonFunction和in Classes
in classes表示采样次数,次数越多获取的人脸的次数越多,但更容易框错
返回值是矩形的坐标,每个矩形为一个人脸(默认的人脸检测器)
"""
#返回训练好的人脸68特征点检测器
predictor = dlib.shape_predictor('D:/GoogleDownload/shape_predictor_68_face_landmarks.dat')
return detector,predictor
#获取检测器
detector,predictor=get_detector_and_predicyor()
def painting_sunglasses(img,detector,predictor):
#给人脸带上墨镜
rects = detector(img_gray, 0)
for i in range(len(rects)):
landmarks = np.matrix([[p.x, p.y] for p in predictor(img,rects[i]).parts()])
right_eye_x=0
right_eye_y=0
left_eye_x=0
left_eye_y=0
for i in range(36,42):#右眼范围
#将坐标相加
right_eye_x+=landmarks[i][0,0]
right_eye_y+=landmarks[i][0,1]
#取眼睛的中点坐标
pos_right=(int(right_eye_x/6),int(right_eye_y/6))
"""
利用circle函数画圆
函数原型
cv2.circle(img, center, radius, color[, thickness[, lineType[, shift]]])
img:输入的图片data
center:圆心位置
radius:圆的半径
color:圆的颜色
thickness:圆形轮廓的粗细(如果为正)。负厚度表示要绘制实心圆。
lineType: 圆边界的类型。
shift:中心坐标和半径值中的小数位数。
"""
cv2.circle(img=img, center=pos_right, radius=30, color=(0,0,255),thickness=1)#红色边框
cv2.circle(img=img, center=pos_right, radius=30, color=(0,0,0),thickness=-1)#黑色
for i in range(42,48):#左眼范围
#将坐标相加
left_eye_x+=landmarks[i][0,0]
left_eye_y+=landmarks[i][0,1]
#取眼睛的中点坐标
pos_left=(int(left_eye_x/6),int(left_eye_y/6))
cv2.circle(img=img, center=pos_left, radius=30, color=(0,0,255),thickness=1)#红色边框
cv2.circle(img=img, center=pos_left, radius=30, color=(0,0,0),thickness=-1)#黑色
camera = cv2.VideoCapture(0)#打开摄像头
ok=True
# 打开摄像头 参数为输入流,可以为摄像头或视频文件
while ok:
ok,img = camera.read()
# 转换成灰度图像
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
#display_feature_point(img,detector,predictor)
painting_sunglasses(img,detector,predictor)#调用画墨镜函数
cv2.imshow('video', img)
k = cv2.waitKey(1)
if k == 27: # press 'ESC' to quit
break
camera.release()
cv2.destroyAllWindows()
总结
SVM是一个二类分类器,它的目标是找到一个超平面,使用两类数据离超平面越远越好,从而对新的数据分类更准确,即使分类器更加健壮。
支持向量(Support Vetor):就是离分隔超平面最近的哪些点。
寻找最大间隔:就是寻找最大化支持向量到分隔超平面的距离,在此条件下求出分隔超平面。
数据分类类别:
1)线性可分
2)线性不可分
下面首先分析线性可分的情况。
SVM特点
1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射;
2)对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心;
3)支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。因此,模型需要存储空间小,算法鲁棒性强;
4)无任何前提假设,不涉及概率测度;
5)SVM算法对大规模训练样本难以实施
由于SVM是借助二次规划来求解支持向量,而求解二次规划将涉及N阶矩阵的计算(N为样本的个数),当N数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian等的SOR算法
6)用SVM解决多分类问题存在困难
经典的支持向量机算法只给出了二类分类的算法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。可以通过多个二类支持向量机的组合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树;再就是通过构造多个分类器的组合来解决。主要原理是克服SVM固有的缺点,结合其他算法的优势,解决多类问题的分类精度。如:与粗集理论结合,形成一种优势互补的多类问题的组合分类器。
参考
https://blog.csdn.net/sinat_31824577/article/details/51329744
https://blog.csdn.net/sinat_35512245/article/details/54984251
https://blog.csdn.net/sinat_31824577/article/details/51329744
https://cungudafa.blog.csdn.net/article/details/93493229
https://blog.csdn.net/cungudafa/article/details/93397735