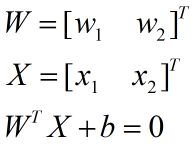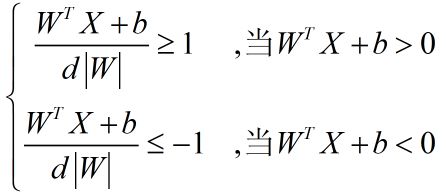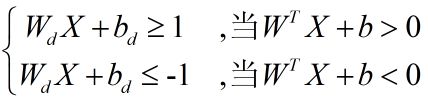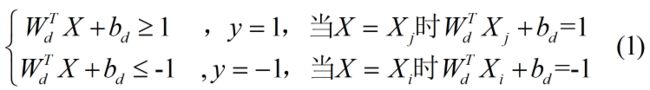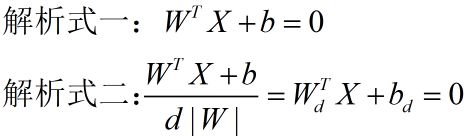图像识别之初探SVM分类器
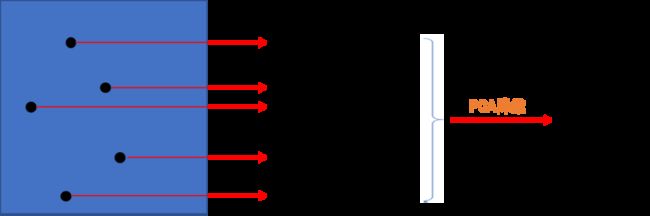
SVM的中文名为支持向量机,是一种非常经典的有监督数据分类算法,也即该算法首先需要训练,训练得到分类模型之后,再使用分类模型对待分类数据进行分类。有监督数据分类算法的大致过程如下图所示:
上图中,训练数据与待分类数据通常为n维向量,n可以是1,2,3,4,5,......
对于图像,一般有两种方法把其所有像素点的像素值转换为n维向量:
方法一:图像数据属于二维矩阵,可以直接把二维矩阵的多行数据按行进行首尾拼接,组成只有一行的n维向量。这种做法通常是在图像尺寸很小的情况,如果图像很大,那么得到的n维向量长度会很长,不仅严重影响训练和分类的速度,有时候数据量过多反而对分类起干扰作用,影响分类的准确性。
方法二:提取图像的特征,包括Sift、Surf特征和Hog特征等。
(1) 检测Hog特征,对于相同尺寸的图像和相同的输入参数,检测得到Hog特征的维数是一样的, 因此Hog特征可直接作为n维向量输入分类器。
(2) 检测Sift特征,Sift特征是对图像上特殊点(可以理解为具有明显特征的角点)的向量描述,每个特殊点的Sift特征为一个128维向量。然而使用Sift算法在不同图像上检测到的特殊点的个数往往是不一样的,此时不同图像的128维向量的个数也不一样,因此不同图像中所有128维向量首尾拼接组成的n维向量的长度也不一样了。如果向量长度不一样,是不能输入分类器的,为了保证每张图像的特征向量长度一致,PCA降维就派上用场了,通常使用PCA降维算法把多个128维向量降维成1个128维向量。
(3) 检测Surf特征,Surf算法是由Sift算法改进和演变而来的,Surf算法主要比Sift算法更快,一个Surf特征为一个64维向量,检测到多个Surf特征之后,也需要像检测Sift特征那样,进行PCA降维,确保每张图像的特征向量维度一致。
最近本人一直在琢磨SVM的数学原理,还有不少地方没能理解,比如求最优解的数学原理、怎么做到多类的分类、核函数等。下面首先以二维向量为例,来讲讲我对SVN分类器的初步理解(扩展到n维也是一样的原理),然后再讲解怎么使用Opencv的SVM模块对手写数字图片和Cifar-10数据集进行分类。
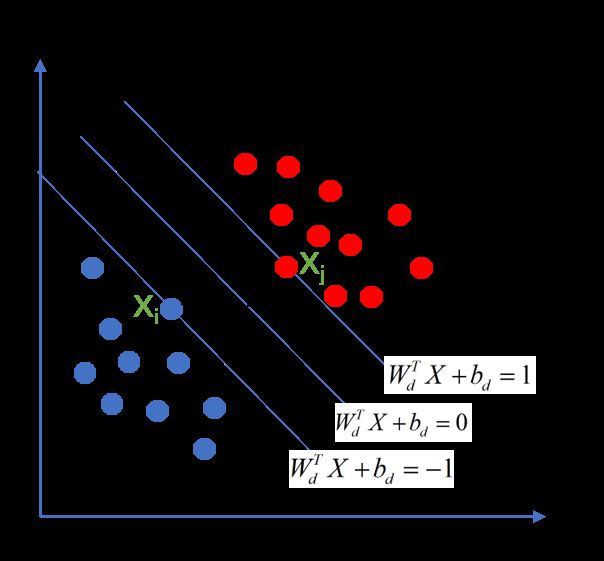
假设有多个二维向量如下:
以上的每个二维向量在x1-x2平面坐标系中表现为一个点,我们的目标是使用一条直线把这些点分成两类,两类中距离最近的点分别为Xi和Xj,我们要寻找的直线在Xi和Xj的中间,也即Xi和Xj到直线的距离都为d,当d取得最大值的时候,这条直线就是我们要找的分类界限啦~
在我们最常见的x-y坐标系中,直线的一般形式为Ax+By+c=0。同理,在x1-x2坐标系中,我们分别使用w1代替A,w2代替B,x1代替x,x2代替y,b代替C,得到直线的一般表达式为w1x1+w2x2+b=0,写成向量形式:
根据点到直线的距离公式,有d的计算式:
由于d是最短距离,对于所有点均满足:
也即有:
对上式,不等号两边都除以d,则有:
我们记:
于是有:
为了方便分类,我们通常给每个点(二维向量)贴上一个标签y,属于红点则y=1,属于蓝点则y=-1,从几何原理来看,有:
1. 当WTX+b>0时点位于直线上方,属于红点类型,此时y=1;
2. 当WTX+b<0时点位于直线下方,属于蓝点类型,此时y=-1。
所以上式又可以转换为:
y的绝对值为1,因此y相当于正负号的作用,由此上式可以合并为:
我们注意到,在x1-x2坐标系中,由于d|W|是一个大于零的实数,以下两个解析式表示的是同一条直线:
因此,问题可以等效转换为求使d取得最大值的以上的解析式二。
此时同样由点到直线的距离公式可得d的计算式为:
又由以上的(1)式可得:
由上式可知当|Wd|取得最小值时,d取得最大值,因此问题又可以等效转换为求下式的最小值,之所以这样转换,使为了后续方便通过求导来求得最优解:
推导到这里,由以上的(2)式和(3)式,我们就可以得到SVM最优化问题的数学表达了:
(1) 约束条件:对x1-x2坐标系中所有的点Xk (k=1,2,3,4,5,......),均满足:
(2) 在满足以上约束条件的前提下,求解(3)式的Wd。
本文的原理就讲到这里,关于如何求得以上数学问题的最优解,我们后续再继续研究和讲解。下面我们来讲讲如何使用Opencv得SVM模块来对手写数字图像和Cifar-10图像进行分类。关于如何获取手写数字图像和Cifar-10图像,此处不再重复,读者如果感兴趣可以参考我之前的博文:
https://blog.csdn.net/shandianfengfan/article/details/109665320
https://blog.csdn.net/shandianfengfan/article/details/109882511
首先是对手写数字图像进行训练和分类,由于手写数字图像特征相对简单,且尺寸为较小的20*20,因此我们使用以上提到的方法一把每张图像数据转换为一个n维向量,再把n维向量输入SVM模块中。代码如下:
void SVM_Hand_Digital_test(void)
{
char ad[128] = { 0 };
int testnum = 0, truenum = 0;
Ptr model = SVM::create(); //创建一个SVM分类器
model->setType(SVM::C_SVC); //设置SVM类型
model->setKernel(SVM::LINEAR); //设置核函数,这里使用线性核
model->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, 1000, 1e-6)); //设置求SVM最优解的最大迭代次数和精度
Mat traindata, trainlabel;
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 400; j++)
{
sprintf_s(ad, "%d/%d.jpg", i, j);
Mat srcimage = imread(ad);
srcimage = srcimage.reshape(1, 1); //将多行数据转换为一行的向量
traindata.push_back(srcimage); //将向量输入到训练矩阵中
trainlabel.push_back(i); //将标签输入到标签矩阵中
}
}
traindata.convertTo(traindata, CV_32F); //将训练数据转换为浮点型数据
model->train(traindata, ROW_SAMPLE, trainlabel); //输入训练数据和标签,开始训练分类模型
for (int i = 0; i < 10; i++)
{
for (int j = 400; j < 500; j++)
{
testnum++;
sprintf_s(ad, "%d/%d.jpg", i, j);
Mat testdata = imread(ad);
testdata = testdata.reshape(1, 1); //将多行数据转换为一行的向量
testdata.convertTo(testdata, CV_32F); //将待分类数据转换为浮点型数据
Mat result;
int response = model->predict(testdata); //使用训练得到的分类模型对待分类数据进行预测,得到分类结果
if (response == i) //如果预测的分类结果与标签一致,则认为分类成功
{
truenum++;
}
}
}
cout << "测试总数" << testnum << endl;
cout << "正确分类数" << truenum << endl;
cout << "准确率:" << (float)truenum / testnum * 100 << "%" << endl;
}
运行以上代码,得到结果如下。训练之后,对1000张手写数字图像进行预测分类,准确率达到90.5%,这个分类结果还是比较理想的。
接下来,我们再使用Opencv的SVM模块对Cifar-10数据集进行分类。我们使用以上提到的方法二把每张图像转换为一个n维向量:提取每张图像的Hog特征,并把Hog特征输入SVM模块。首先在data_batch_1.bin~data_batch_5.bin这个5个文件中都取前900张图像对SVM模型进行训练,然后再对test_batch.bin中的前800张图像进行预测分类。代码如下:
void SVM_cifar_test_hog(void)
{
char ad[128] = { 0 };
int testnum = 0, truenum = 0;
Ptr model = SVM::create(); //创建一个SVM分类器
model->setType(SVM::C_SVC); //设置SVM类型
model->setKernel(SVM::RBF); //设置核函数,这里使用非线性核RBF
model->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, 1000, 1e-6)); //设置求SVM最优解的最大迭代次数和精度
Mat traindata, trainlabel;
const int trainnum = 900;
//定义HOG检测器
HOGDescriptor *hog = new HOGDescriptor(cvSize(16, 16), cvSize(8, 8), cvSize(8, 8), cvSize(2, 2), 9); //特征提取滑动窗口, 块大小, 块滑动步长, 胞元(cell)大小
vector descriptors; //定义HOG特征数组
const int win_step = 16;
//加载data_batch_1.bin的训练数据
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < trainnum; j++)
{
printf("i=%d, j=%d\n", i, j);
sprintf_s(ad, "cifar/batch1/%d/%d.tif", i, j);
Mat srcimage = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(srcimage, descriptors, Size(win_step, win_step), Size(0, 0)); //计算图像的HOG特征
Mat hogg(descriptors); //将特征数组存入Mat矩阵中
srcimage = hogg.reshape(1, 1); //将多行数据转换为一行的向量
traindata.push_back(srcimage); //将HOG特征向量加载到训练矩阵中
trainlabel.push_back(i); //将标签输入到标签矩阵中
}
}
//加载data_batch_2.bin的训练数据
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < trainnum; j++)
{
printf("i=%d, j=%d\n", i, j);
sprintf_s(ad, "cifar/batch2/%d/%d.tif", i, j);
Mat srcimage = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(srcimage, descriptors, Size(win_step, win_step), Size(0, 0));
Mat hogg(descriptors);
srcimage = hogg.reshape(1, 1); //Mat Mat::reshape(int cn, int rows = 0),cn表示通道数,为0则通道不变,rows表示矩阵行数
traindata.push_back(srcimage);
trainlabel.push_back(i);
}
}
//加载data_batch_3.bin的训练数据
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < trainnum; j++)
{
printf("i=%d, j=%d\n", i, j);
sprintf_s(ad, "cifar/batch3/%d/%d.tif", i, j);
Mat srcimage = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(srcimage, descriptors, Size(win_step, win_step), Size(0, 0));
Mat hogg(descriptors);
srcimage = hogg.reshape(1, 1); //Mat Mat::reshape(int cn, int rows = 0),cn表示通道数,为0则通道不变,rows表示矩阵行数
traindata.push_back(srcimage);
trainlabel.push_back(i);
}
}
//加载data_batch_4.bin的训练数据
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < trainnum; j++)
{
printf("i=%d, j=%d\n", i, j);
sprintf_s(ad, "cifar/batch4/%d/%d.tif", i, j);
Mat srcimage = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(srcimage, descriptors, Size(win_step, win_step), Size(0, 0));
Mat hogg(descriptors);
srcimage = hogg.reshape(1, 1); //Mat Mat::reshape(int cn, int rows = 0),cn表示通道数,为0则通道不变,rows表示矩阵行数
traindata.push_back(srcimage);
trainlabel.push_back(i);
}
}
//加载data_batch_5.bin的训练数据
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < trainnum; j++)
{
printf("i=%d, j=%d\n", i, j);
sprintf_s(ad, "cifar/batch5/%d/%d.tif", i, j);
Mat srcimage = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(srcimage, descriptors, Size(win_step, win_step), Size(0, 0));
Mat hogg(descriptors);
srcimage = hogg.reshape(1, 1); //Mat Mat::reshape(int cn, int rows = 0),cn表示通道数,为0则通道不变,rows表示矩阵行数
traindata.push_back(srcimage);
trainlabel.push_back(i);
}
}
traindata.convertTo(traindata, CV_32F); //将训练数据转换为浮点型数据
model->train(traindata, ROW_SAMPLE, trainlabel); //输入训练数据和标签,开始训练分类模型
//对test_batch.bin中的前800张图像进行预测分类
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 800; j++)
{
testnum++;
sprintf_s(ad, "cifar/test_batch/%d/%d.tif", i, j);
Mat testdata = imread(ad, CV_LOAD_IMAGE_GRAYSCALE);
hog->compute(testdata, descriptors, Size(win_step, win_step), Size(0, 0)); //计算待分类图像的HOG特征
Mat hogg(descriptors);
testdata = hogg.reshape(1, 1);
testdata.convertTo(testdata, CV_32F);
Mat result;
int response = model->predict(testdata); //对Hog特征进行预测分类
if (response == i) //如果预测的分类结果与标签一致,则认为分类成功
{
truenum++;
}
}
}
cout << "测试总数" << testnum << endl;
cout << "正确分类数" << truenum << endl;
cout << "准确率:" << (float)truenum / testnum * 100 << "%" << endl;
}
运行以上代码,得到结果如下。对8000张图像进行分类,准确率只有55.2375%,分类的准确率与前文中我们使用KNN算法的分类结果相比,并不没有提升多少。当图像复杂之后,这些传统的数据分类算法就显得有些无力了。因此在以后的文章中,我们将尝试卷积神经网络与深度学习来进行分类。
以上只是总结了一下本人对SVM算法的初步理解,本人远没有达到理解透的境界,但是学无止境,让我们继续加油吧~~
微信公众号如下,欢迎扫码关注,欢迎私信技术交流: