【人工智能与机器学习】——聚类（学习笔记）

前言：我们之前学习的算法均是有监督学习（supervised learning），它的一个鲜明特征是通过给定的标签来学习从数据特征（如图像）到语义标签的映射关系。但在很多实际问题中，数据并没有语义标签，解决此类问题就要用到无监督学习（unsupervised learning）。
无监督学习有很多技术方向，聚类（clustering）是其中一个重要的方向。聚类的本质就是把特征相近的数据样本放到一起，达到“人以群分，物以类聚”的效果。将聚类应用在社交网络上，可以根据上网习惯特征，把行为习惯类似的用户归为同一组别，以便向同一组别的用户推荐相同的产品。

---

1. 什么是聚类

在决策树这篇文章中，我们借助决策树解决了预测打网球的问题，分类算法中样本数据的种类是已知的，即天气、温度、湿度、风速。聚类算法不同于分类算法，它在操作时并不知道样本数据有多少种类，而是通过数据分析，发现数据之间的内在联系和相关性，将看似没有关联的事物聚合在一起，并将数据划分成若干集合，方便为数据打上标签（隐式标签），从而进行后续的分析和处理。其中，被划分的数据集合称作簇（cluster）。可以用作数据预处理。

2. K-均值（K-means）聚类算法

在机器学习中，有很多种划分数据集的方法，其中最常用的一种是基于数据间距离的K - 均值算法。所谓基于距离，指的是如果把数据呈现在坐标系中，数据集中的每个样本都是空间中的一个点坐标，通过简单的计算就可以知道各个点之间的距离，距离越近，即相似程度越高。

K - 均值算法是一个迭代算法，需要经过多次重复计算才能得到最终的结果。值得注意的是，由于样本数据不同，特征值的波动范围和计量单位很可能不一致。为了消除不同量纲的特征值对计算结果产生的影响，可以在使用K - 均值算法之前，对样本数据作归一化处理。

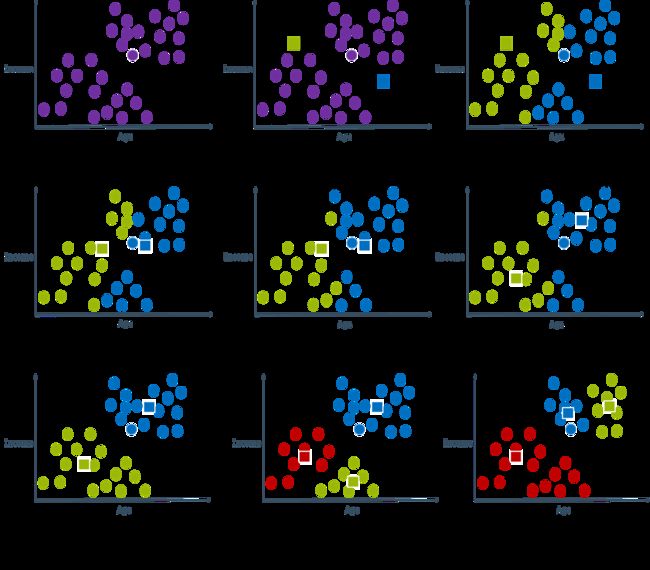
K - 均值算法的具体步骤如下：
（1）随机选取$K$个样本点作为$K$个初始簇的质心（centroid）。
（2）计算其他每个样本点到这$K$个质心的距离。对于每一个样本$X_n$，找到离它最近的质心${\lambda }_n$，将$X_n$划分到第${\lambda }_n$个簇中，并将$X_n$的簇标签置为${\lambda }_n$。
（3）当所有样本所属的簇都更新完毕之后，对于更新后的每个簇计算其包含的所有样本的平均向量（中心点)，作为新的质心。
（4）重复上面的（2）（3）步，迭代至所有质心都不变化为止。

举例：根据客户的收入和收入对用户聚类（发现用户类别）

3. 聚类的评价指标

我们需要通过某种性能指标来评价聚类的好坏。聚类的性能度量大致有两类:一类是将聚类结果与参考模型（baseline model）进行比较，称为外部指标（external in-dex)；另一类是直接评估聚类结果而不利用任何参考模型，称为内部指标（internal in-dex)。
本期只介绍两种常用的内部指标：
一种是簇内平方和（Sum of Squared Error，SSE），又叫作Inertia：
$$\sum _{i=1}^n{\left(x_i-C_k\right)}^2$$

每个数据点（$x_i$）距其聚簇中心（$C_k$）的距离平方和，值越小表示聚簇越紧密，质量较高。

另一种是轮廓系数（Silhouette Coefficient）：
$$S=\frac{b-a}{\max (a,b)}$$
对每个数据点计算一个轮廓系数：

• a 表示此数据点到同簇中所有其他点的平均距离，簇内凝聚度(越小越好)
• b 表示此数据点到最近簇中所有点的平均距离，簇间分离度(越大越好)

将所有数据点的轮廓系数取平均值就得到一个总的评分，取值在[-1, 1]之间，值越大，聚类效果越好

3.1 初始聚簇中心的选择方法

随机地选取一点作为起始点（如图），计算每个点与已有聚簇中心点之间的最短距离$D(x)$，按照$\frac{D(x{)}^2}{\sum D(x{)}^2}$的概率选取下一个点（目的：离已选初始点远点）

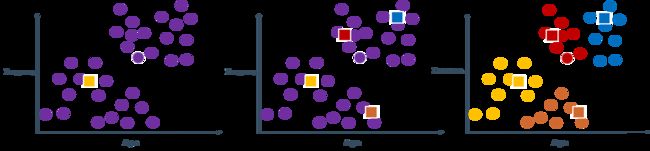
这就是K-means++，是对K-mean随机初始化质心的一个优化。

4. K值的选择方法

有时应用中有一个K：

• 将相似的任务聚集在四个CPU核上 (K=4)
• 一款球鞋设计了10种不同鞋码以适合不同的人 (K=10)
• 一个视频网站可以浏览20种不同分区的视频 (K=20)

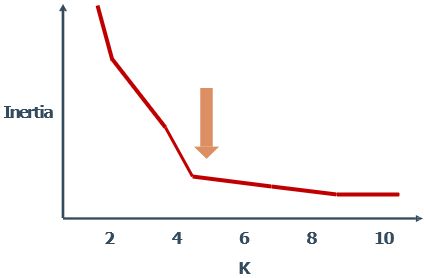
4.1 手肘法

Inertia衡量点到聚簇中心的距离，值会随着K的增大而不断降低，只要聚簇密度在不断增大，小于真实K值时，下降幅度很大；超过真实K值时，下降趋于平缓

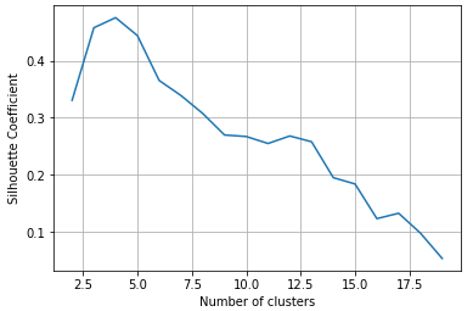
4.2 轮廓系数法

取轮廓系数的最大值

5. 语法

导入包含聚类方法的类：

from sklearn.cluster import KMeans

创建该类的一个对象：

kmeans = KMeans(n_clusters=3, init='k-means++')		# n_clusters即最终的聚簇数，kmeans++初始化方法

拟合数据，并在新数据上预测聚簇：

kmeans = kmeans.fit(X1)
y_predict = kmeans.predict(X2)

也可以用MiniBatchKMeans使用批处理方式

在线文档： K-means的语法

6. 距离指标

距离指标的选择对聚类的成功至关重要，每个指标有各自的优点和适用情况，但有时距离指标的选择也是基于经验性的评价

以下几种距离在K近邻那篇讲过，这里不再赘述

传送门：【人工智能与机器学习】——K近邻（KNN）与模型选择（学习笔记）

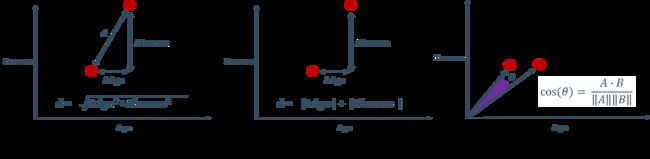
欧几里得vs.余弦距离

• 欧几里得距离适用于基于坐标的度量
• 余弦距离更适合那些出现位置不重要的数据，例如文本数据
• 欧几里得距离对维度灾难更敏感

6.1 杰卡德距离（Jaccard）

杰卡德距离:衡量两个集合差异性的一种指标，是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数(定义为两个集合交集的元素个数除以并集的元素个数。)。

应用于集合（例如单词的出现）
句子 A: “I like white-cut chicken.”
set A = { I，like，white-cut，chicken }
句子 B: “Do you want white-cut chicken or braised chicken?”
set B = { Do，you，want，white-cut，chicken，or，braised }

$$1-\frac{A\cap B}{A\cup B}=1-\frac{\mathrm{len}(\text{ shared })}{\text{ len }(\text{unique })}$$

根据公式，我们可以求出上面两个句子的相似度
句子 A: “I like white-cut chicken.”
set A = { I，like，white-cut，chicken }
句子 B: “Do you want white-cut chicken or braised chicken?”
set B = { Do，you，want，white-cut，chicken，or，braised }

$$1-\frac{A\cap B}{A\cup B}=1-\frac{2}{9}$$

6.2 语法

导入一般的两两距离计算函数：

from sklearn.metrics import pairwise_distances

计算距离：

dist = pairwise_distances(X,Y,metric='euclidean')	# 选择的距离指标（这里是欧氏距离）

其他的距离指标选择有：cosine, manhattan, jaccard，等等
距离指标函数也可以被专门导入，如：

from sklearn.metrics import euclidean_distances

7. 聚合式层次聚类

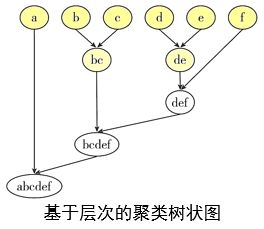
作为聚类算法的一种，层次聚类（hierarchical clustering）通过计算不同类别数据点之间的相似度形成一棵具有层次结构的树。树的聚集有自底向上聚合策略，也有自顶向下分裂策略。层次聚类算法多采用自底向上的聚合策略

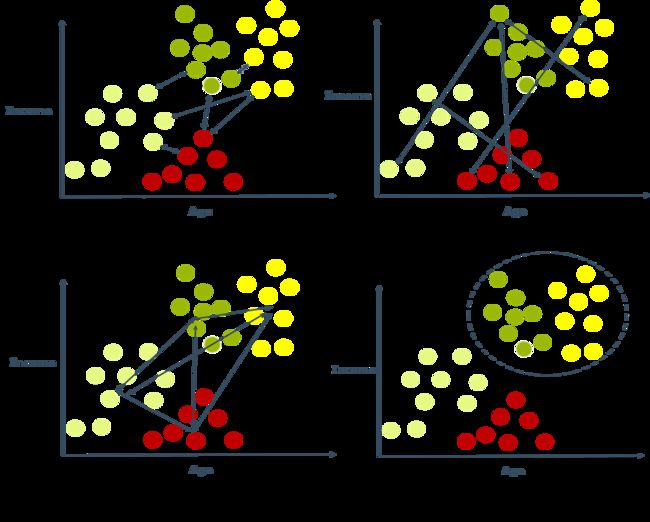
以凝聚的层次聚类算法（Agglomerative Nesting，AGNES）为例，它先将数据集中的每个样本看作一个初始聚类簇，然后再逐步将它们两两合并，直到获得最终的聚类结果。

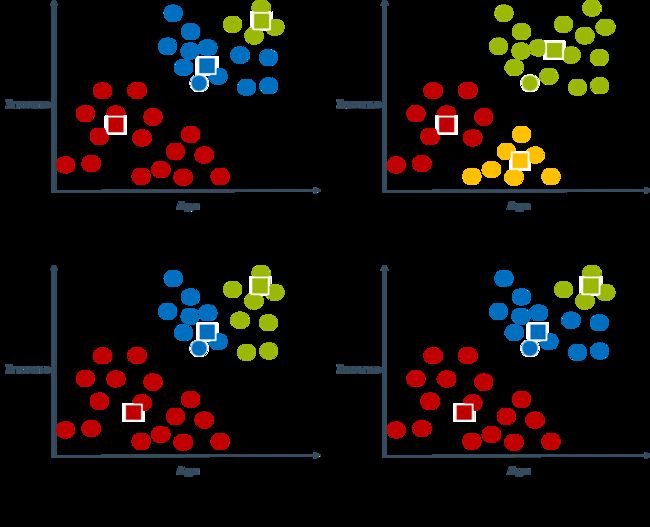
还是这个例子：根据客户的收入和收入对用户聚类（发现用户类别）

应该选哪个K值最合适呢？

7.1 停止条件

条件1：达到正确的聚类数
条件2：最小平均聚簇距离达到预设的值

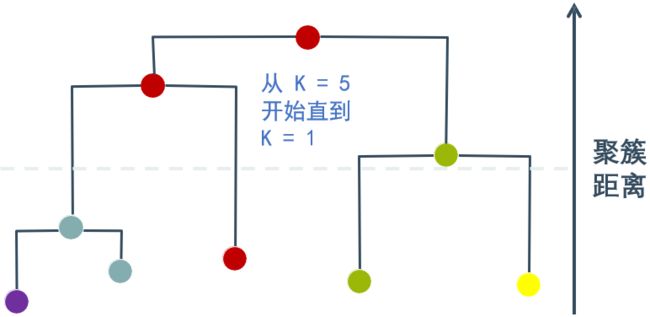
令AGNES 算法一直执行到所有样本出现在同一个簇中，即k = 1，则可得到如图所示的“树状图”（dendrogram），其中每层链接一组聚类簇。

7.2 簇间距离的类型

• 单链接（Single Linkage）：簇间最小的两点距离
• 完全链接（Complete Linkage）：簇间最大的两点距离
• 平均链接（Average Linkage）：簇间所有两点距离的平均值
• Ward链接（Ward Linkage）：每次选择导致最佳Inertia的合并

7.3 语法

导入包含聚类方法的类：

from sklearn.cluster import AgglomerativeClustering

创建该类的一个对象：

agg = AgglomerativeClustering(n_clusters=3,affinity='euclidean',  linkage='ward')		
# n_clusters表示最终的聚簇数；affinity和linkage表示聚簇间距离的计算和聚合方法

拟合数据，并预测新数据的聚簇：

agg = agg.fit(X1)
y_predict = agg.predict(X2)

在线文档： 聚合式层次聚类的语法

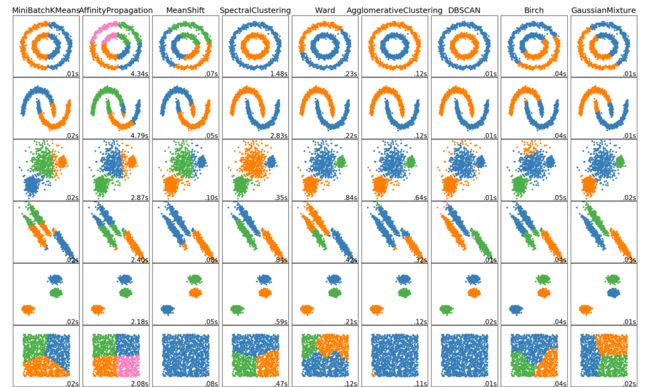
其他聚类算法

8. 综合案例：商场客户聚类

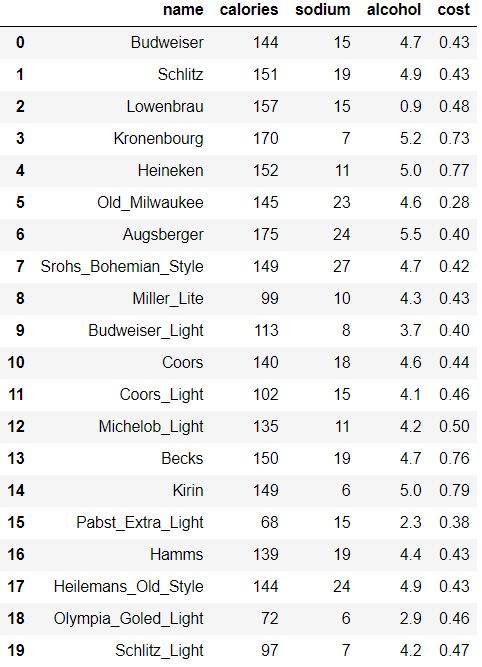
给定一个啤酒的数据集，每条数据是一种啤酒，包含它的卡路里、钠、酒精含量以及价格。目标是对所给啤酒进行聚类。具体操作为：

# beer dataset
import pandas as pd
url = 'beer.txt'
beer = pd.read_csv(url, sep=' ')
beer

聚类，把除name之外的所有属性当作输入特征。

# 准备输入特征 X
X = beer.drop('name', axis=1)

# 初始化一个3个聚簇的K-means聚类算法,对输入数据进行聚类。
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=1)
km.fit(X)

KMeans(algorithm=‘auto’, copy_x=True, init=‘k-means++’, max_iter=300, n_clusters=3, n_init=10, n_jobs=1, precompute_distances=‘auto’, random_state=1, tol=0.0001, verbose=0)

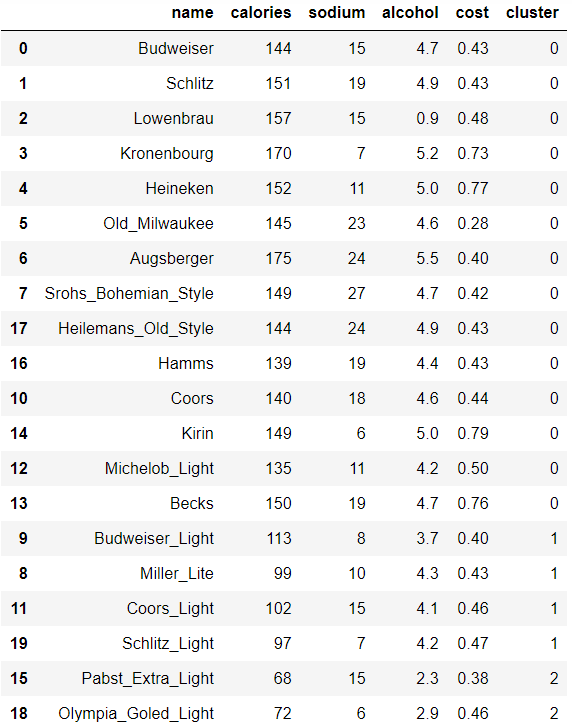
查看以及可视化聚类结果。把聚类的结果标签拼接到原始数据的最后，并按照聚类标签排序显示。

# save the cluster labels and sort by cluster
beer['cluster'] = km.labels_
beer.sort_values(by='cluster')

# 查看聚簇中心点
km.cluster_centers_

$$\begin{gathered} array([[150.,17.,4.52142857,0.52071429], \\ [102.75,10.,4.075,0.44], \\ [70.,10.5,2.6,0.42]]) \end{gathered}$$

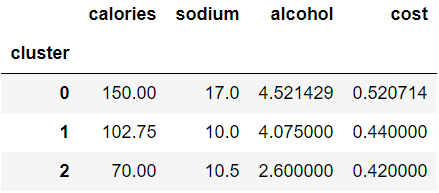
# 查看每个聚类的每维特征上的平均值（即聚簇中心点）。
centers = beer.groupby('cluster').mean()
centers

可视化聚类结果：

%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14
# 创建一个颜色数组用于可视化
import numpy as np
colors = np.array(['red', 'green', 'blue', 'yellow'])
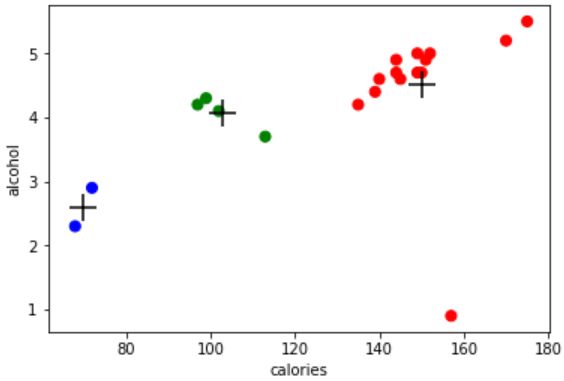
# 绘制（卡路里，酒精）散点图(0=red, 1=green, 2=blue)
plt.scatter(beer.calories, beer.alcohol, c=colors[beer.cluster], s=50)
# 用同样的散点图方式绘制出聚簇中心点，用黑色的“+"表示
plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')
# 添加标签
plt.xlabel('calories')
plt.ylabel('alcohol')

聚类评价指标

# 计算K=3时的轮廓系数
from sklearn import metrics
metrics.silhouette_score(X_scaled, km.labels_)		# 0.45777415910909475

# 计算聚簇数量从2到19变化时的轮廓系数
k_range = range(2, 20)
scores = []
for k in k_range:
    km = KMeans(n_clusters=k, random_state=1)
    km.fit(X_scaled)
    scores.append(metrics.silhouette_score(X_scaled, km.labels_))

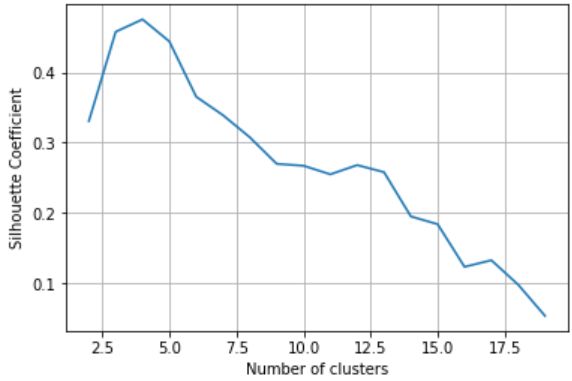
# 可视化不同聚簇数量对应的轮廓系数
plt.plot(k_range, scores)
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Coefficient')
plt.grid(True)

9. 课后习题

1. 【判断题】在采用k-means算法聚类时，只要数据集不变，不管初始质心如何选择，算法收敛时其最终的结果总是相同。

答案：1.×（解析：不可能一样，总会导致局部最优解）

---

OK，以上就是本期知识点“聚类”的知识啦~~ ，感谢友友们的阅读。后续还会继续更新，欢迎持续关注哟~
如果有错误❌，欢迎批评指正呀~让我们一起相互进步
如果觉得收获满满，可以点点赞支持一下哟~

❗ 转载请注明出处
作者：HinsCoder
博客链接： 作者博客主页