机器学习算法基础6-模型保存与加载、逻辑回归、Kmeans(聚类)

一、模型的保存与加载

sklearn模型的加载与保存

API:
from sklearn.externals import joblib

保存与加载API
保存：joblib.dump(rf,'test.pkl')
加载：estimator = joblib.load('test.pkl')

注意：文件格式为.pkl

# sklearn模型的保存与加载
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.externals import joblib
from sklearn.metrics import mean_squared_error

def mylinear():
    '''
    线性回归预测房子价格
    :return:
    '''
    # 一、获得数据
    lb = load_boston()

    # 二、处理数据

    # 1.取得数据集中特征值与目标值
    x = lb.data
    y = lb.target

    # 2.分割数据集  训练集与测试集
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

    # 三、进行特征工程
    # 1.训练集与测试集标准化处理
    # 特征值与目标值都必须进行标准化处理，实例化两个API,分别处理特征值与目标值
    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()
    # 要求传入的y_train是二维数组，后面也一样，用reshape(-1,1)方法转换
    y_train = std_y.fit_transform(y_train.reshape(-1,1))
    y_test = std_y.transform(y_test.reshape(-1,1))

    # 四、线性回归模型-estimator预测

    # 1.正规方程求解方式预测结果
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    # 回归系数
    print('正规方程的回归系数为:\n',lr.coef_)

    # 保存训练好的模型
    joblib.dump(lr, 'test.pkl')

    # 预测测试集房子的价格,
    y_predict = std_y.inverse_transform(lr.predict(x_test))
    print('正规方程预测测试集房子的价格:\n',y_predict)
    # 回归性能评估
    y_test = std_y.inverse_transform(y_test)
    print('正规方程的回归性能评估为:',mean_squared_error(y_test, y_predict))

if __name__ == '__main__':
    mylinear()

# sklearn模型的保存与加载
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.externals import joblib
from sklearn.metrics import mean_squared_error

def mylinear():
    '''
    线性回归预测房子价格
    :return:
    '''
    # 一、获得数据
    lb = load_boston()

    # 二、处理数据

    # 1.取得数据集中特征值与目标值
    x = lb.data
    y = lb.target

    # 2.分割数据集  训练集与测试集
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

    # 三、进行特征工程
    # 1.训练集与测试集标准化处理
    # 特征值与目标值都必须进行标准化处理，实例化两个API,分别处理特征值与目标值
    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()
    # 要求传入的y_train是二维数组，后面也一样，用reshape(-1,1)方法转换
    y_train = std_y.fit_transform(y_train.reshape(-1,1))
    y_test = std_y.transform(y_test.reshape(-1,1))

    # 四、
    # 模型加载预测房价结果
    model = joblib.load('test.pkl')
    # 预测测试集房子价格
    y_model_predict = std_y.inverse_transform(model.predict(x_test))
    print('保存模型预测房价结果\n',y_model_predict)

    # # 四、线性回归模型-estimator预测
    #
    # # 1.正规方程求解方式预测结果
    # lr = LinearRegression()
    # lr.fit(x_train, y_train)
    # # 回归系数
    # print('正规方程的回归系数为:\n',lr.coef_)
    #
    # # 保存训练好的模型
    # joblib.dump(lr, 'test.pkl')
    #
    # # 预测测试集房子的价格,
    # y_predict = std_y.inverse_transform(lr.predict(x_test))
    # print('正规方程预测测试集房子的价格:\n',y_predict)
    # # 回归性能评估
    # y_test = std_y.inverse_transform(y_test)
    # print('正规方程的回归性能评估为:',mean_squared_error(y_test, y_predict))

if __name__ == '__main__':
    mylinear()

二、逻辑回归-分类算法

1.逻辑回归介绍

逻辑回归是解决二分类问题的利器

# 案例
1.广告点击率
2.判断用户的性别
3.预测用户是否会购买给定的商品类
4.判断一条评论是正面的还是负面的

逻辑回归的输入：

2.逻辑回归损失函数

逻辑回归的损失函数、优化

与线性回归原理相同,但由于是分类问题，损失函数不一样，只能通过梯度下降求解

举例：

[样本1，样本2，样本3，样本4]

逻辑回归预测是          阈值为0.5
[[0.6]     1
[0.1]      0
[0.51]     0
[0.7]]     1

类似信息熵的计算按结果为
-[1*log(0.6) + 1*log(0.9) + 1*log(0.49) + 1*log(0.7)]
信息熵越小越好，损失越小，越确定

损失函数：
均方误差：不存在多个局部最低点，只存在一个最小值
对数似然函数：多个局部最小值（这个目前解决不了）---梯度下降法特点

优化方向
1.多次随机初始化，多次比较最小值结果
2.求解过程当中，调整学习率

尽管没有全局最低点，但是效果还是不错的

3.逻辑回归API

sklearn逻辑回归API:sklearn.linear_model.LogisticRegression

sklearn.linear_model.LogisticRegression(penalty=‘l2’, C = 1.0)
# 自带正则化，解决过拟合问题，  penalty=‘l2’    C = 1.0

Logistic回归分类器
coef_：回归系数

4.LogisticRegression回归案例-良／恶性乳腺癌肿瘤预测

样本比例：良性（65.5%）  恶性（34.5%）

根据样本数量大小判定，哪个类别少，判定概率值是指这个类型。本案例为恶性(正例)，
即概率为0.6则为恶性，概率为0.1则为良性

良／恶性乳腺癌肿分类流程：

1、网上获取数据（工具pandas）
2、数据处理-数据缺失值处理
3、特征工程-特征处理-标准化
4、LogisticRegression估计器流程

andas的使用:
pd.read_csv(’’,names=column_names)

column_names：指定类别名字,['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion',
                'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
return:数据
# 方法
# 替代缺失值
replace(to_replace=’’,value=)：返回数据
dropna():返回数据

# 逻辑回归做二分类进行癌症预测
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report

def logistic():
    '''
    逻辑回归做二分类进行癌症预测(根据细胞属性特征)
    :return:
    '''
    # 一、读取数据
    # 构造列标签列表
    column_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape','Marginal Adhesion',
                    'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses', 'Class']
    # names参数指定列名
    data = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data',
                names=column_names)
    print(data)

    # 二、数据处理
    # 1.缺失值进行处理-替代
    data = data.replace(to_replace='?', value=np.nan)
    # 删除
    data = data.dropna()

    # 2.取特征值与目标值
    y = data[column_names[10]]
    x = data[column_names[1:10]]

    # 3.数据集分割-训练集与测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 三、特征工程
    # 1.标准化处理
    std = StandardScaler()
    # 特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 四、逻辑回归预测
    # 正则化系数C是超参数，可以调优
    lg = LogisticRegression(C=1.0)

    lg.fit(x_train, y_train)
    # 回归系数
    print('回归系数:\n', lg.coef_)

    y_predict = lg.predict(x_test)
    # 预测准确率
    print('准确率:\n',lg.score(x_test, y_test))

    # 每个类别的精确率与召回率
    # labels=[2, 4], target_names=['良性', '恶性'] 2与良性对应，4与恶性对应
    print('每个类别的精确率与召回率是:\n', classification_report(y_test, y_predict, labels=[2, 4], target_names=['良性', '恶性']))

    return None

if __name__ == '__main__':
    logistic()

# 回归系数:
#  [[1.34896921 0.1584493  0.88149942 0.79523126 0.33072118 1.07917493
#   1.03709744 0.51162748 0.303647  ]]
# 准确率:
#  0.9766081871345029

# 每个类别的精确率与召回率是:
#                precision    recall  f1-score   support
#
#           良性       0.95      0.98      0.97       101
#           恶性       0.97      0.93      0.95        70

5.LogisticRegression总结

LogisticRegression总结：

应用：广告点击率预测、是否患病、金融诈骗、是否为虚假账号、电商购物搭配推荐
优点：适合需要得到一个分类概率的场景，简单、速度快
缺点：当特征空间很大时，逻辑回归的性能不是很好
（看硬件能力）

softmax方法-逻辑回归在多分类问题上的推广，将在后面的神经网络算法中介绍

6.判别模型与生成模型

三、k-means-聚类-(非监督学习算法)

1.k-means步骤

聚类：
K：把数据划分成多少个类别
若不知道类别个数-超参数

k-means步骤：
1、随机设置K个特征空间内的点作为初始的聚类中心
2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别
3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）
4、如果计算得出的新中心点与原中心点一样，那么结束聚类；
  否则根据新的中心点重复第二步操作

k-means API:sklearn.cluster.KMeans

sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
# k-means聚类

# 参数
n_clusters:开始的聚类中心数量
init:初始化方法，默认为'k-means ++’

labels_:默认标记的类型，可以和真实值比较（不是值比较）

2.聚类案例-用户对物品种类喜好分析

k-means对Instacart Market用户聚类：

1、降维之后的数据
2、k-means聚类
3、聚类结果显示

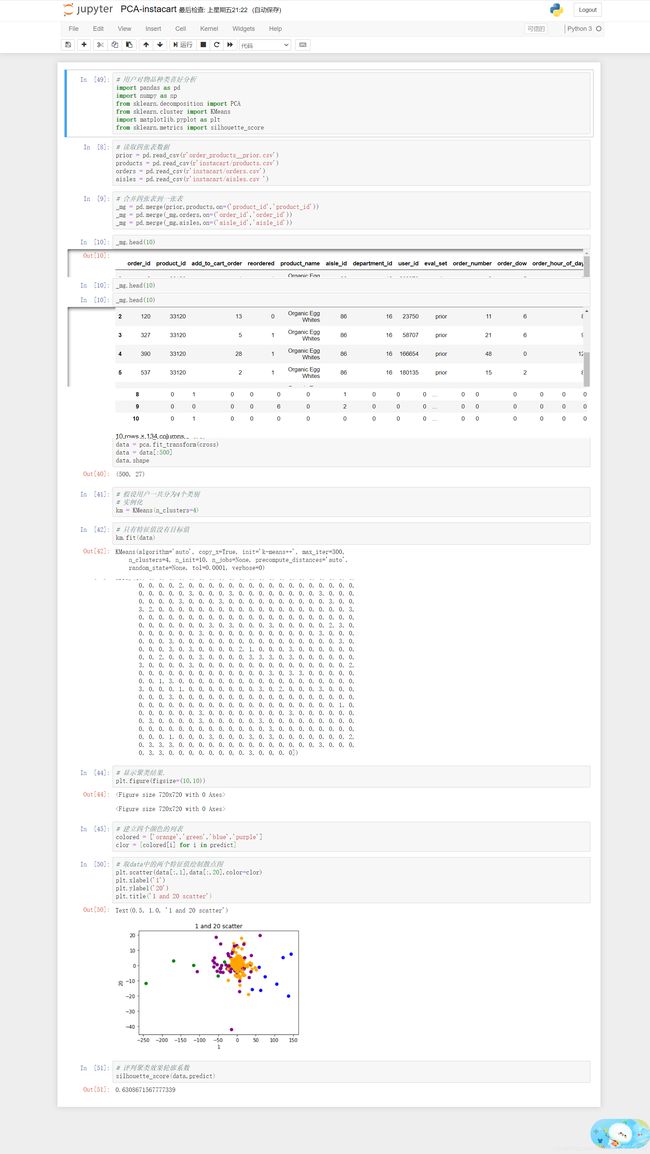
3.Kmeans性能评估指标

如果sc_i 小于0，说明a_i 的平均距离大于最近的其他簇。
聚类效果不好
如果sc_i 越大，说明a_i 的平均距离小于最近的其他簇。
聚类效果好
轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优

4.Kmeans性能评估指标API

Kmeans性能评估指标API:sklearn.metrics.silhouette_score

# 计算所有样本的平均轮廓系数
sklearn.metrics.silhouette_score(X, labels)

# 参数
X：特征值
labels：被聚类标记的目标值

5.kmeans总结

Kmeans总结：

特点分析：采用迭代式算法，直观易懂并且非常实用
缺点：容易收敛到局部最优解(多次聚类)，需要预先设定簇的数量(k-means++解决)

注意：聚类一般在分类前