广度优先算法解决8数码问题【c++】

8数码问题 （广度优先算法解决----c++）

8数码问题问题描述

八数码问题也称为九宫问题，在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格（空格用0来表示），空格周围的棋子可以移到空格中。

要求解的问题是：
给出一种初始布局（初始状态）和目标布局（目标状态），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

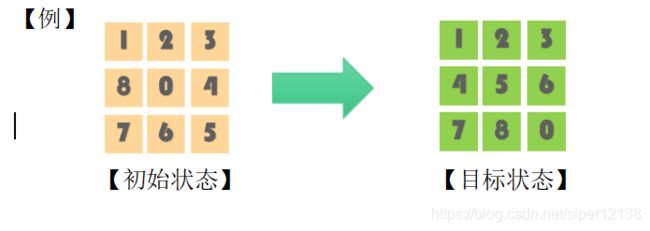
问题分析

八数码问题的核心在于移动棋子使其得到需要的状态分布（即目标状态），为便于控制操作，我们将每次移动棋子的过程都视为标号为0的棋子与其相邻棋子的位置交换操作。（如下图，2移动到0，和0移动到2，进行了一样的操作，交换0和2的位置）

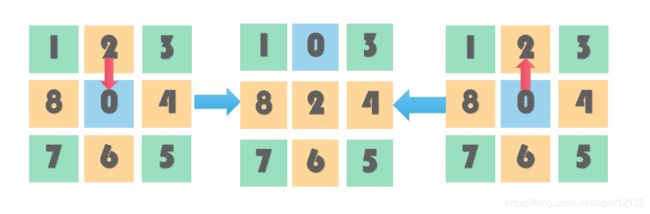
我们以空格（0号棋子）为操作对象，将其与周围棋子交换位置。求解棋子移动过程的问题可以转化为求空白格（0号棋）移动过程。（如下图1，0可以和他周围的2，8，6，4交换位置，图2，0可以和他周围的1，2，3交换位置，图3，0可以和他周围的1，8交换位置，）

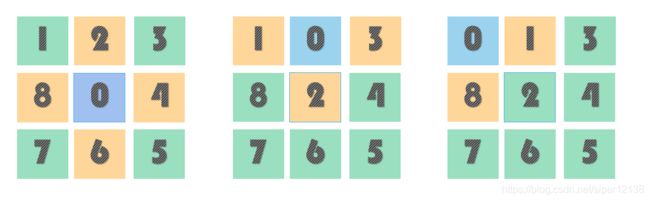
0号棋子移动过程只涉及到上移，下移，左移，右移四条法则。根据移动法则，从初始状态出发可以建立搜索树，求解问题其实就是求解最短路径问题。

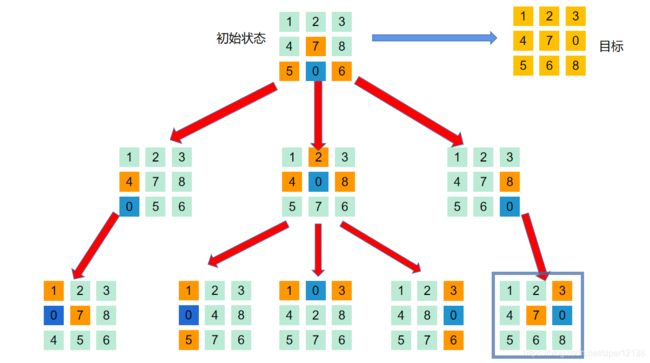
广度优先算法

求解最短路径的问题考虑使用广度优先搜索算法（BFS，其英文全称是Breadth First Search。），所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实验里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）

1.算法执行过程

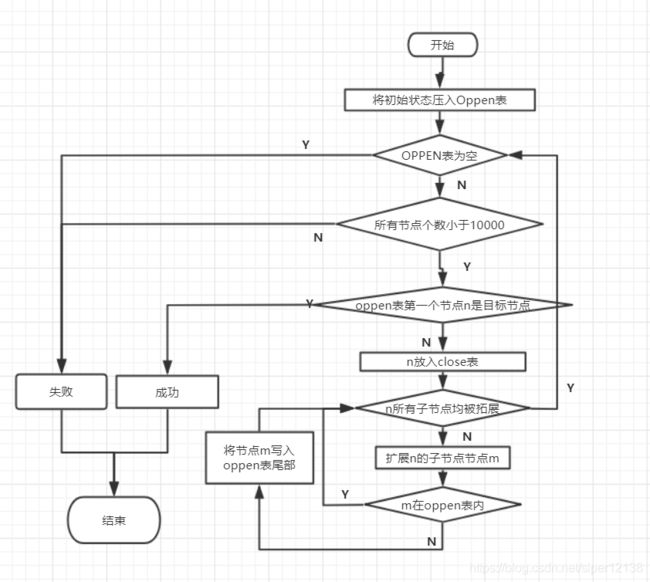
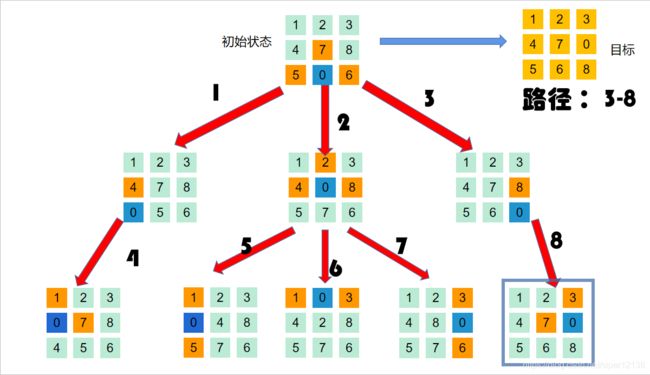
2.为算法实现的概念图：（黑色加粗数字为节点拓展顺序）

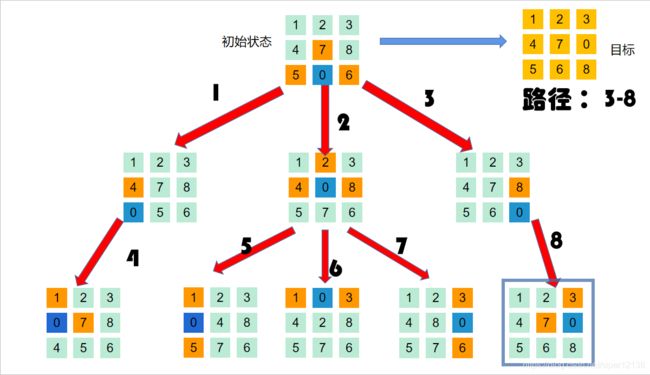
3.算法的优点：
广度优先搜索算法对于解决最短路径问题非常有效，搜索深度较小，每个节点只访问一次，节点总是以最短的结点总是以最短路径被访问，所以第二次路径确定不会比第一次短。

4.算法的缺点
广度优先搜索算法坚决最短路径问题虽然非常有效，但是解决问题需要非常庞大的内存空间，当路径较长或者节点过多时，会有非常巨大的内存开销，并且运行时间会非常长。
坚决方案：当节点数达到一定值时，默认该问题无解，停止算法。

编程环境及语言

语言：c++
环境：vs2019

代码实现

定义相关节点结构体：

定义相关变量和函数：

核心函数实现：

核心函数核心算法实现：

算法设置目标状态：

代码详情

/*
==============================================================
                   广度优先算法解决8数码问题                
==============================================================

输入示例： 1_3_2_4_5_7_6_8_0[回车]   （下划线表示空格）
对应的8数码九宫格状态    |1|3|2|                           
                        |4|5|7|                           
                        |6|8|0|  
						
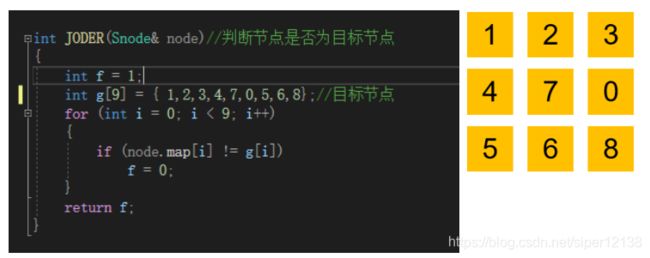
		目标状态		    |1|2|3|
						|4|5|6|
						|7|8|0|

                【 0 表示九宫格的空白格 】
==============================================================


*/
#include 
using namespace std;

#define MAX_OPEN_LEN 50000
#define MAX_CLOSE_LEN 50000

struct Snode//节点结构体
{
	int parent;  //指向该结点父节点的编号
	int map[9];
public:
	void In(const int* d);
	void Out(int* d);
};
void Snode::In(const int* d)
{

	for (int i = 0; i < 9; ++i)
		map[i] = d[i];
}

Snode OPEN[MAX_OPEN_LEN];//OPEN表
int op = 0;
Snode CLOSE[MAX_CLOSE_LEN];//close表
int cp = 0;                //扩展的节点数
int result[50000][9];     //result数组用于保存路径


int YONNEW(Snode& , Snode& );     //判断是否为新节点        返回值 1: 是  0: 不是
int FIND(const int* );         //广度优先运行函数   
inline void  CHANGE(int& , int& );//交换俩个数              
int JODER(Snode& );        //判断节点是否为目标节点  返回值 1: 是  0: 不是

int main(void)
{
	int m[9] = {0};//初始化
	cout << "==============================================================" << endl;
	cout << "                    广度优先算法解决8数码问题                 " << endl;
	cout << "==============================================================" << endl;
	cout << "示例： 1_3_2_4_5_7_6_8_0[回车]   （下划线表示空格）          "  << endl;
	cout << endl;
	cout << "对应的8数码九宫格状态   |1|3|2|  目标状态：  |1|2|3|          " << endl;
	cout << "                        |4|5|7|              |4|5|6|          " << endl;
	cout << "                        |6|8|0|              |7|8|0|          " << endl;
	cout << endl;
	cout << "【注意】工程生产节点多于10000个视为无解                       " << endl;
	cout << "==============================================================" << endl;
	cout << "成功案例参考 ：[123564780]  [123456780]                           " << endl;

	cout << "失败案例参考 ：[756482310]  [156234780] " << endl;
	
	cout << "==============================================================" << endl;
	cout << "请按照示例输入8数码初始状态:";

	for (int i = 0; i < 3; i++)//输入
		for (int j = 0; j < 3; j++)
			cin >> m[3 * i + j];

	FIND(m);//运行
	return 0;
}

int YONNEW(Snode& node1, Snode& node2)  //判断是否为新节点
{
	int f = 1;
	for (int i = 0; i < 9; i++)
	{
		if (node1.map[i] != node2.map[i]) f = 0;
	}
	return f;
}

inline void CHANGE(int& a, int& b)//交换俩个数
{
	int t = a;
	a = b;
	b = t;
}

int JODER(Snode& node)//判断节点是否为目标节点
{
	int f = 1;
	int g[9] = { 1,2,3,4,5,6,7,8,0};//目标节点
	for (int i = 0; i < 9; i++)
	{
		if (node.map[i] != g[i])
			f = 0;
	}
	return f;
}

int FIND(const int* d)//运行函数
{
	int begin = 0;                    //begin含义是每次从OPEN表中去除要扩展的那个节点
	int node_number = 1;              //扩展节点数，初始时已有OPEN[0]节点,故为1
	static int dp[4] = { -3,-1,1,3 }; 
	//-3上，3下，-1左，1右

	op = 1;
	cp = 0;
	OPEN[begin].In(d);
	OPEN[begin].parent = -1;  

	//OPEN表不为空
	while (op > 0)
	{
		int i = 0, KONGE, pos, j = 0, k = 0;
		//找目标节点
		if (JODER (OPEN[begin]) == 1)  
		{
			cout << endl;
			cout << endl;
			cout << "==============================================================" << endl;
			cout <<  endl;
			cout << "                    成功得到正确解，路径如下：                " << endl;
			cout << endl;
			cout << "———————————————————————————————" << endl;
			CLOSE[cp] = OPEN[begin];

			//路径存入数组result中，目标节点--->根节点
			while (begin != -1)         
			{
				for (int i = 0; i < 9; i++)
				{
					result[j][i] = OPEN[begin].map[i];
				}
				j = j + 1;
				begin = OPEN[begin].parent;
			}

			//result数组中路径输出，根节点--->目标节点
			for (i = j - 1; i >= 0; i--)       
			{
				for (k = 0; k < 9; k++)
				{
					cout << result[i][k] << " ";
					if (k % 3 == 2)  cout << endl;
				}
				cout << endl;
			}
			cout << "=============================================================="  << endl;
			cout << "生成的节点总数为           ||           " << node_number << endl;
			cout << "扩展的节点总数为：         ||           " << cp << endl;
			cout << "==============================================================" <<  endl;

			return 1;
		}
		for (KONGE = 0; KONGE < 9; ++KONGE)
		{
			if (OPEN[begin].map[KONGE] == 0)
				break;                        //跳出当前for循环，向下执行
		}
		for (i = 0; i < 4; ++i)
		{   //判断空白位置位置怎样可以移动，与上边的判断相同
			if (KONGE == 0 && (i == 0 || i == 1))  continue;     
			if (KONGE == 1 && i == 0)         continue;
			if (KONGE == 2 && (i == 0 || i == 2))  continue;
			if (KONGE == 3 && i == 1)         continue;
			if (KONGE == 5 && i == 2)         continue;
			if (KONGE == 6 && (i == 1 || i == 3))  continue;
			if (KONGE == 7 && i == 3)         continue;
			if (KONGE == 8 && (i == 2 || i == 3))  continue;
			pos = KONGE + dp[i];
			//交换位置
			CHANGE(OPEN[begin].map[KONGE], OPEN[begin].map[pos]); 
			Snode child;
			child.In(OPEN[begin].map);
			//判断是否为新节点
			for (j = 0; j < cp; ++j)      
			{
				if (YONNEW(CLOSE[j], child) == 1)
					break;
			}
			//得到新节点
			if (j == cp)                         
			{
				OPEN[op] = child;             //先使用op,再op加1
				OPEN[op].parent = begin;
				op++;
				node_number++;
				//无解，这里当op等于10000时退出，并返回0
				if (node_number == 10000)                             //无解，这里当op等于10000时退出，并返回0
				{
					cout << endl;
					cout << endl;
					cout << "==============================================================" << endl;
					cout << endl;
					cout << "           警告：                节点过多视为无解             " << endl;
					cout << endl;
					cout << "==============================================================" << endl;
					
					return 0;
				}
			}
			//前边把OPEN[min]的值进行了交换，现在再换回去，保持OPEN[min]的map数组
			CHANGE (OPEN[begin].map[KONGE], OPEN[begin].map[pos]);    
		}
		CLOSE[cp++] = OPEN[begin];
		begin = begin + 1;
	}

	return 0;
}

算法测试

算法输入初始状态：

测试结果


如上图，理论结果与算法结果一致，算法适应性较好。

算法其他运行实例
设置目标状态为：

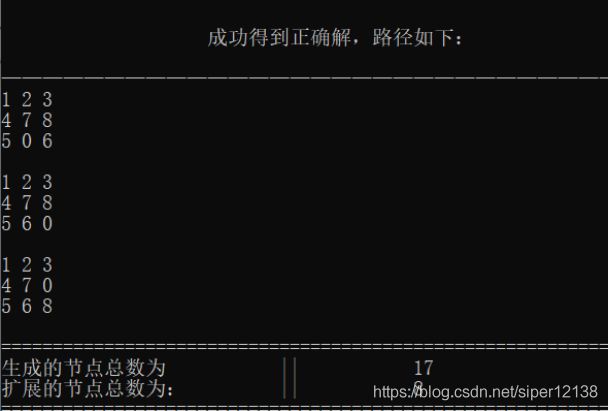
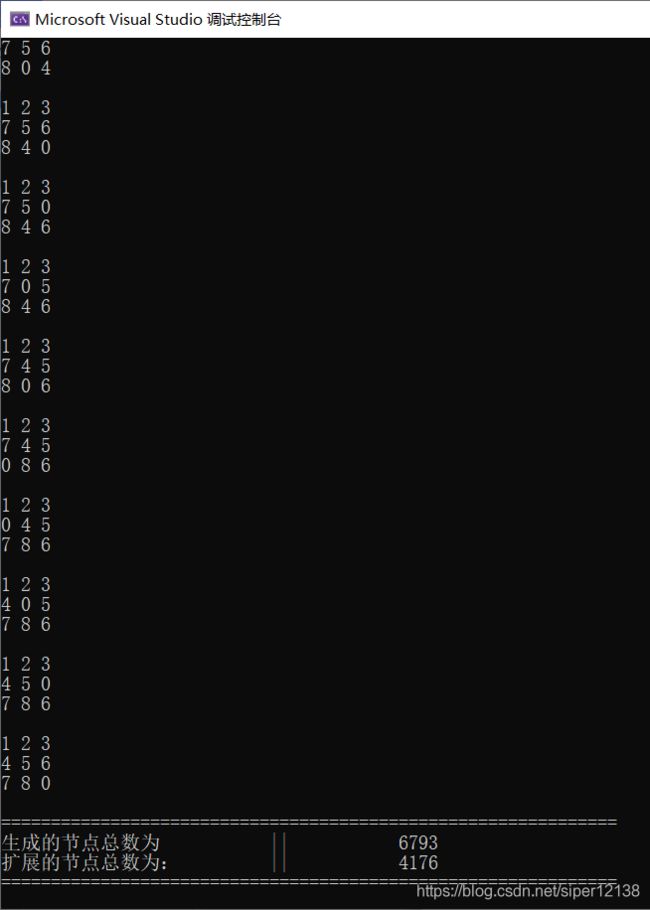
1.成功案例
（1）初始状态为 123456780

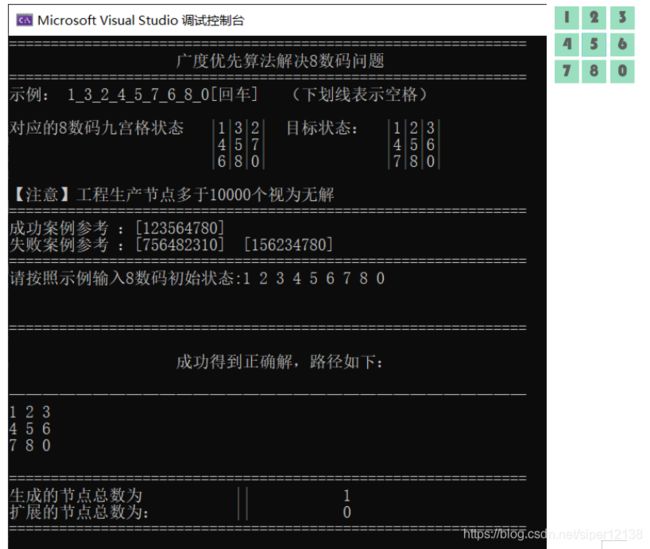（2）初始状态为 123564780


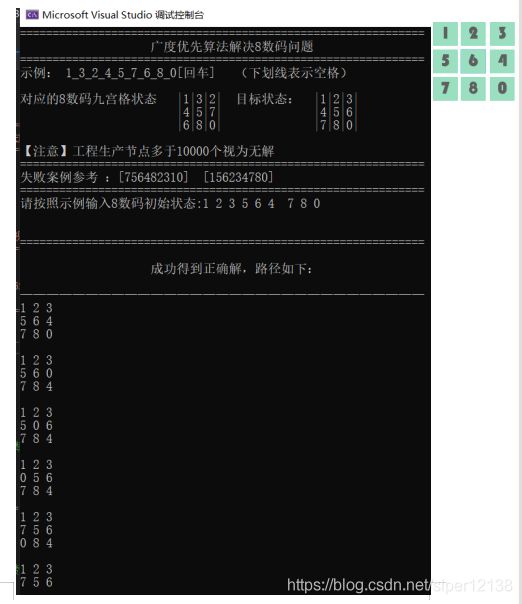
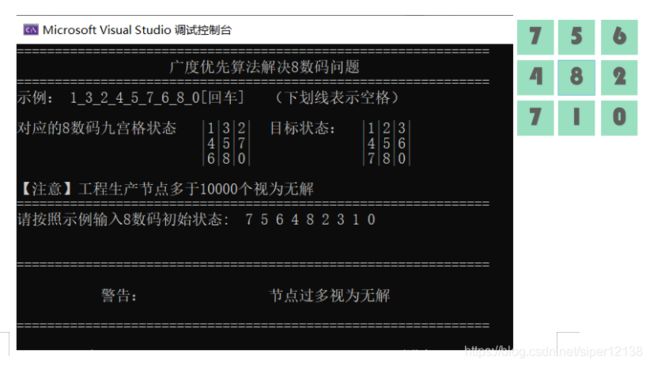
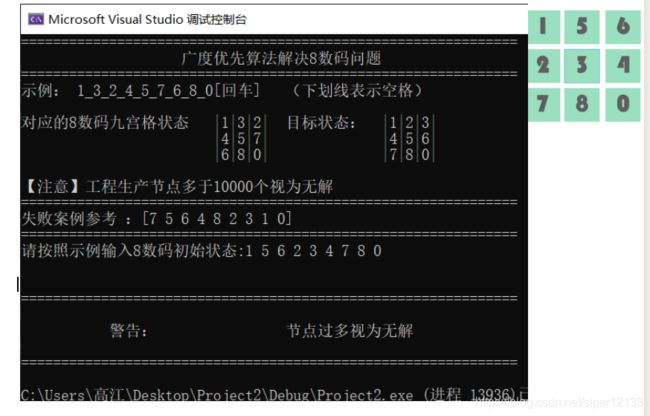
2.失败案例
（1）初始状态为 123564780

（2）初始状态为756482310

心得体会

设计算法解决问题的过程一定要抓住核心，定好操作对象，才能更好的解决问题。从算法到代码实现的过程也是一个复杂的过程，需要用到很多其他的知识储备比如数据结构等等。

希望这篇文章可以帮助刚接触算法的同学更好的理解广度优先算法。同时也希望自己可以在编程这条路上有所成就。