2019年数维杯数学建模B题火灾等级评价与快速救援措施优化求解全过程文档及程序

2019年数维杯数学建模

B题 火灾等级评价与快速救援措施优化

原题再现：

  随着人类经济社会的快速发展，人类的各项活动影响了地球演进的自然规律。这使得全球极端气候频发，各类自然灾害的数量与等级均有一定的上升趋势。

  众所周知“水火无情”，没有科学合理的火灾救援策略不仅会增加无辜人员伤亡，同时也会带来重大经济灾难。2019年清明节前后因北方大部分地区具有较大等级的风，春季气候普遍干燥，使得众多地区发生了一定规模的火灾。2018年美国的加州大火所造成的经济损失相当于烧掉了整个洛杉矶。这就意味着科学的火灾等级的评价及救援策略的引进是十分有必要的。

  本题目以附件2中的数据为基础数据试解决如下几个问题：

  问题1：请你对附件2中的2033个火灾预期危害等级进行评价，并筛选出10大火灾编号。

  问题2：结合问题1中所确定的火灾等级及火灾位置，请您筛选出重点的放火位置。

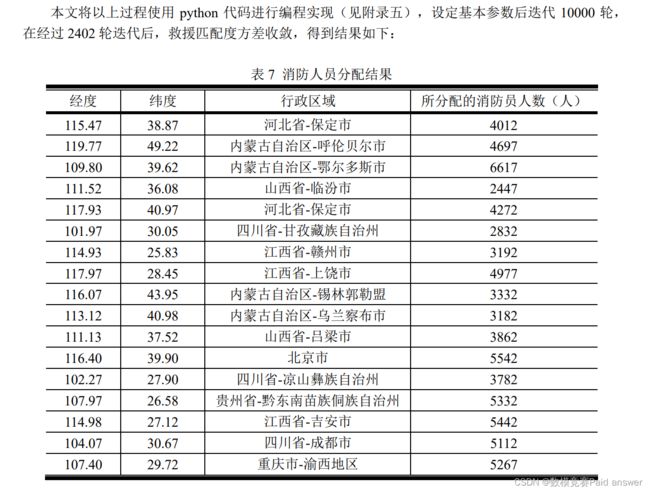
  问题3：假设目前有100000个消防人员，请您将这些人员合理的分配到问题2中所筛选出的重点位置中。

整体求解过程概述(摘要)

  火的使用推动了人类的进步，然而一旦失控则将演化为火灾。火灾可能发生在任何地方，城市、森林、草原火灾都会对地区经济造成很大的影响，甚至威胁到人类的生命安全，良好的火灾等级评价方案及消防人员分配方案将大大降低火灾带来的危害。
  对于问题一，针对不同火灾发生特点的多样性，本文首先对数据进行预处理，并通过火灾发生的经纬度获取其卫星地图及火灾所属行政区域信息。通过判断火灾发生位置的地形情况，将火灾分为农作物火灾、森林火灾、草原火灾及城市火灾四类。针对不同火灾的类型特点建立对应的评价模型，植被燃烧考虑横向扩散，城市建筑燃烧考虑纵向扩散，并采用回归拟合方法确定燃烧扩散时间与风力及救援难度的关系，从而建立火灾危害等级评价模型。最后，本文将问题给出的数据代入模型进行计算，评定火灾的危害等级，并筛选出 10 大火灾。
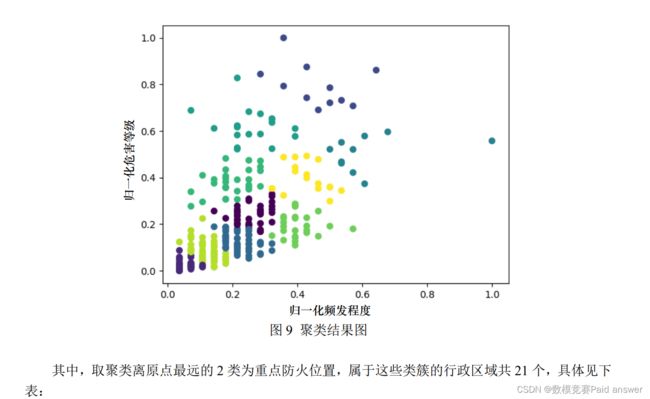
  对于问题二，为了合理筛选出火灾重点防护位置，针对火灾的危害等级、频度及所属行政区域位置因素，本文按照地级市划分出 311 个火灾所属行政区域，对行政区域统计火灾危害及频度信息，在两个维度上使用 k-means 聚类，最终在 10 个结果类簇中选取危害等级及频度相对较高的 2 个类簇共 21 个行政区域作为重点防火位置。
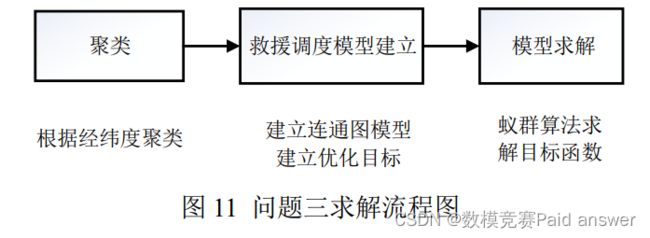
  对于问题三，为了合理安排火灾消防人员，针对问题二中重点防火位置的地理分布特点及火灾危害等级的影响，考虑到地区间消防人员的互相调配情况，本文建立多连通分支无向图模型用以表征重点防火区域间的关联关系，通过对经纬度信息聚类将重点防火位置映射到 3 个连通分支中，并对每个连通分支建立连通关系。使用距离表征连通分支中边的权值，并基于此建立救援调度模型。将危害等级与消防人员的分配关系定义为救援配比度，将优化救援配比度方差作为求解目标，使用蚁群算法求解得到 21 个行政区域消防人员数量的最优分配。

问题分析：

  这是一个评价规划问题，根据火灾初始面积、风力大小、预期蔓延速度、救援难度等已知指标及从经纬度挖掘得到的区域及火灾类型等隐藏指标研究火灾造成的危害及损失，判断已有记录的火灾中哪些是对人类经济社会造成重大损失的火灾。同时，需要根据评价得到的结果合理安排固定数量的消防员，这需要考虑不同位置区域的相关联程度等因素。问题的特点在于指标的可挖掘信息丰富；问题的难点在于选择合理的指标量化方法，对于火灾危害等级建立普适的评价及消防人员规划模型。
  问题一要求对已知的 2033 个火灾进行危害等级评价，这需要从问题已给的指标中挖掘对评价具有一定价值的指标，建立合适的评价模型。由于问题已经给了一定量的数据，本文通过三个步骤解决该问题。首先对数据预处理筛除定位结果为空值的数据与经纬度定位在国外的数据；其次根据经纬度通过 Python 爬虫程序将 Google 地图上的卫星地图块收集到本地，并根据收集到的地图块判断火灾发生的地形信息，从而对已给的火灾数据进行分类；最后对于不同的分类采用数学方法建立适当的评价模型，统一每个类型的评价系数使其整体具有普适性。
  问题二要求结合问题一求得的每个火灾危害等级及其发生的位置信息，筛选出重点防火位置。本文结合火灾的防护需要考虑到该地区火灾的频发程度及火灾的危害程度两个维度，对第一问求得的 311 个二级行政区域统计火灾发生数量及火灾危害等级，在两个维度上归一化后进行聚类，得到一系列的类簇用以综合表征该地区火灾防护的需求等级。
  问题三要求将固定量的消防员合理分配到问题二筛选出的重点位置中。由于已经有了问题一的评价度量，同时能够从问题二的结果中获得这些位置的地理信息。本文对这些重点位置建立连通图模型，同时采用聚类方法确定连通分支，考虑在同一连通分支内的重点位置能够互相调配消防员参与救援。通过衡量火灾损失与消防员人数匹配程度求得最优的分配方案。

模型假设：

  1.假设相同评价体系下火灾的发生不受季节影响。
  2.假设火灾预计蔓延速度不受地形因素影响。
  3.假设初始着火面积为正圆形，并在各个方向上的扩散速度相同。

模型的建立与求解

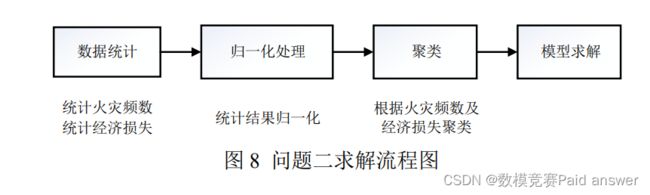
  问题一需要对已知的火灾进行危害等级评价。为了建立合理、普适的火灾危害等级评价模型，本文首先对已知数据进行预处理，将不合理数据筛除；然后根据火灾发生的经纬度对火灾所属的行政区域进行划分，同时通过计算机程序处理的方法获取火灾地点卫星成像特征图，将火灾划分为 4个主要类型；最后使用数学方法对这 4 个主要类型建立评价模型，并将已知数据代入模型计算筛选出 10 大火灾。问题求解流程如下图：

  Step1 数据预处理
  为了方便后续步骤的进行，ᨀ高模型精度，本文首先根据经纬度定位，通过使用 GeoPy[2]
调用百度地图 API 对数据进行预处理（程序见附录一），筛除的数据满足如下规则：
  1）通过经纬度无法查询到位置所在行政区域信息；
  2）通过经纬度查询到的位置在中国边界范围之外。
  经过预处理，删除数据 50 项，最终保留数据 1983 项。具体结果参见支撑材料：火灾数据.xlsx。
  Step2 数据划分
  为了方便问题二对火灾重点位置的筛选及问题三对 100000 名消防人员的划分，本文使用 GeoPy查询经纬度信息获得火灾发生地点所属的行政区域，统计二级行政区域共 311 个。具体结果参见支撑材料：火灾数据.xlsx。
  同时，为了便于建立合理模型，本文使用 Python 编写爬虫程序（程序见附录二）将 Google 地图卫星成像地图块爬取到本地，然后对地形地貌进行区分。主要的火灾点地形特征示例图如下：

  通过卫星成像图，参考资料中的分类，将预处理之后的火灾数据分为农作物火灾、森林火灾、草原火灾及城市火灾四种主要类型，并对数据进行标注。不同类型的数据量统计如下图：

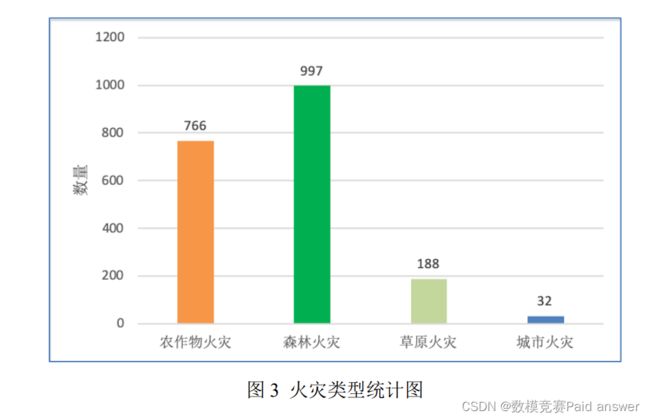
  Step3 模型建立
  通过 Step2 中划分出的农作物火灾、森林火灾、草原火灾及城市火灾的分类，本文对不同的类别分别建立模型。根据资料[4]，火灾事故常常根据直接财产损失或人员伤亡来定级与划分，见下表：

  其中单位面积的价值在 5.1.3 小节中求解得出，这里着重对燃烧总面积建立模型。对于农作物火灾、森林火灾及草原火灾这三类火灾，由于可燃物类型均为植被，其火势蔓延的方式大致相同，由模型假设得到这三类火灾可燃物燃烧示意图如下：


  根据上一小节 Step3 分类建立的模型，需要求解蔓延时间函数及农作物、森林、草原及城市建筑物四种燃烧影响物的单位面积价值。确定评价模型之后，需要对问题给出的数据进行评估，筛选出10 大火灾。本文采用回归拟合方式得到蔓延时间方程，并查阅资料确定了不同火灾分类下影响的单位面积价值，最终确定危害等级评价模型。
  Step1 蔓延时间求解
  火灾蔓延时间影响了火灾向外扩散的面积与过火面积，为定量分析火灾最终的过火面积，需要确定火灾的蔓延时间。火灾的蔓延时间与风力成正相关，风力越大，火灾燃烧时的空气越充足，热量扩散越快，使火势快速向周围扩散。根据实际情况，当火灾发生时，相关部门会根据火灾大小及时派遣救援部队到场救援，救援部队的水扑灭、建立隔离带等行为一定程度抑制火灾的蔓延，但是受实际救援环境影响，火灾的救援难度存在不同的等级，当火灾的救援难度较小时，救援人员能够比较容易的抑制火势的增长，减少火灾的蔓延时间；随着火灾救援难度的增长，救援人员对火灾扩散的抑制作用不断减小，当救援难度过大时，救援人员对火灾扩散的抑制作用相对较小，火灾持续向周边可燃物蔓延，相应的火灾蔓延时间较长。结合文献及实际情况，本文通过对火灾的风力及救援难度进行二次曲线型的建模。

  Step2 确定单位面积价值
  根据文献[5]，农作物价值包括农产品生产价值、社会保障价值、气体调节价值、水土保持功能价值、环境净化价值，同时还具有水资源消耗、化肥农药等带来的环境污染等负向价值，总结来说农作物提供的价值为 1.89606 元/m2。根据文献[6]，森林价值包括林木价值、林下产品价值、气候调节价值、水源涵养价值、土壤保持价值、空气净化价值等，文章对不同省份地区分类，得到森林提供的价值如下表：


  由于已经划分好省份地区，本文也已在上一小节 Step2 中划分好行政区域，在这里不对全国森林价值求解平均值，模型最终将按照省级行政区计算不同森林火灾对应的森林价值。根据文献[7]，草原价值包括食物和原材料生产价值、旅游价值、有机物生产价值、气体调节价值、水土保持价值、水源涵养价值、生物多样性价值、生物控制价值，总结来说草原ᨀ供的价值为15.84595 元/m2。
  根据文献[8]，城市建筑物价值主要由其房地产成本价值决定，并且与该城市的人均 GDP 相关。建筑房地产成本主要由钢筋、砼、门窗、承包商管理费等费用组成，其建筑房地产成本平均为 1914元/m2。本文通过数据库[9]获得城市火灾所在城市的人均 GDP，为合理刻画城市人均 GDP 对城市建筑价值的影响，对城市人均 GDP 进行归一化处理。最终的城市建筑物价值可以由以下方程得出：

  Step3 火灾评估
  通过以上的数据处理及模型建立与求解，编写 python 程序（见附录三）将每个火灾数据条目代入模型计算，得到所有已知火灾条目的危害等级，按照经纬度映射到全国各地区如下图：



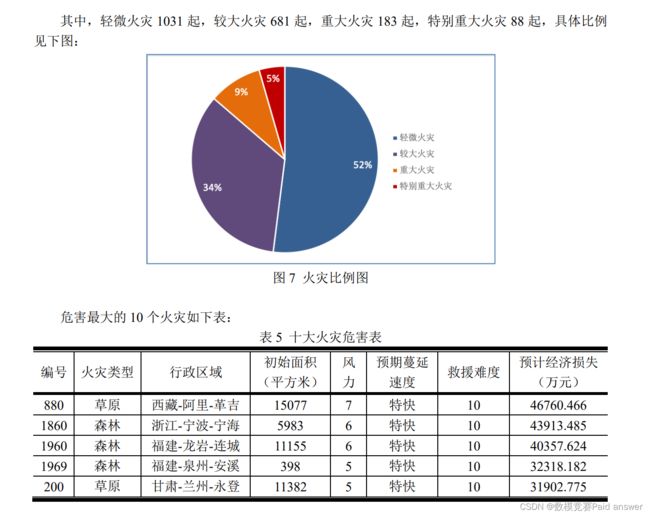
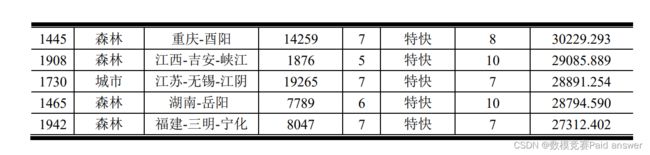
  问题二要求结合问题一中得到的火灾危害等级表及火灾发生的位置，筛选出重点的防火位置。考虑到合理、充分应用已有的信息，本文结合问题一计算得到的火灾危害等级（预计经济损失）及行政区域划分结果，统计每个行政区域所有火灾的危害等级及发生次数，归一化后使用 k-means 聚类，得到每个行政区域位置的火灾防护等级。问题求解流程如下图：

  本文重点考虑区域位置火灾频发程度及火灾危害等级两个维度，对问题一已有结果进行统计，具体统计方案如下

  通过编写 python 程序（见附录四）将上一小节处理好的数据进行聚类，输出的聚类结果如下图：



  问题三要求将 100000 名消防人员合理分配到问题二中所筛选出的重点位置中。本文考虑不同的重点位置在火灾发生时候可能存在消防人员调配支援的现象，首先对问题二中得到的重点位置在地理坐标上聚类，同一类簇中对重点位置间建立连通图模型，以火灾损失与消防员配比作为优化目标，采用蚁群算法求解得到消防人员最优分配。问题的解决流程如下图：

  Step1 聚类
  考虑到地理位置相关性不大的地区在火灾发生时候不互相调配消防员援助救援，本文首先对重点防护位置的经纬度信息聚类，得到的不同类簇间互相不调配消防人员，同一类簇中的重点区域可依据距离调配消防人员。使用 python 编写代码（见附录四）实现对于重点位置的经纬度信息的聚类，其结果如下图：

  Step2 救援调度模型建立


  根据上一小节建立的模型，危害等级（预计经济损失）可以使用问题一的评价模型直接计算得出，因此模型的重点在于可调配人数与连通点常驻人数及边权值（距离）的关系，同时需要求得救援匹配度方差最小的解。本文使用蚁群算法求解最优分配方案。
  Step1 可调配人数方程

  Step2 求解最优分配方案
  对于算法的初始状态，本文先将所有消防人员均匀分配到各个位置，并加上一些噪音值来保证每个位置初始状态的不一致性，每条边累计的信息素量决定了下一次这条边被选中的概率，初始化这些边的信息素都为 0，同时按迭代轮数均匀分配蚂蚁到各个位置，步长定为 5。每轮迭代所有蚂蚁都进行移动操作，每次有向的移动都将带来该条有向边的人员调度，比如蚂蚁从城市 A 移动到城市 B，会将城市 A 中的消防人员个数减少一个步长的人数（即 5 人），同时为城市 B 增加一个步长的人数。蚂蚁移动的方向根据边上的信息素计算的概率得到，具体概率公式如下：

k-means 聚类

# -*- coding: utf-8 -*-
import math
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
if __name__ == '__main__':
 f = open('counter2.txt', 'r')
 cites = []
 c_f = []
 values = []
 maxf = 0
 maxv = 0
 for i in f.readlines():
 tmp = i.strip().split(',')
 cites.append(tmp[0])
 c_f.append(int(tmp[1]))
 values.append(float(tmp[2]))
 if (int(tmp[1]) > maxf):
 maxf = int(tmp[1])
 if (float(tmp[2]) > maxv):
 maxv = float(tmp[2])
 for i in range(len(c_f)):
 c_f[i] = c_f[i] / maxf
 for i in range(len(values)):
 values[i] = values[i] / maxv
 df = pd.DataFrame({'frequency' : c_f, 'value' : values})
 X = df.ix[:,['frequency', 'value']]
 clf_KMeans = KMeans(n_clusters=10)
 counter = [0] * 10
 cluster = clf_KMeans.fit_predict(X)
 index = 0
 f.close()
 f = open('counter2.txt', 'r')
 ff = open('counter3.txt', 'w')
 for i in f.readlines():
 ff.write(i.strip() + ',' + str(cluster[index]) + '\n')
 counter[cluster[index]] = counter[cluster[index]] + 1
 index = index + 1
 plt.figure()
 plt.scatter(X['frequency'],X['value'],c=cluster)
 plt.xlabel(u'归一化频发程度')
 plt.ylabel(u'归一化火灾等级')
 plt.show()

蚁群算法

# -*- coding: utf-8 -*-
from math import radians, cos, sin, asin, sqrt
def haversine(lon1, lat1, lon2, lat2):
 lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])
 dlon = lon2 - lon1
 dlat = lat2 - lat1
 a = sin(dlat/2)**2 + cos(lat1) * cos(lat2) * sin(dlon/2)**2
 c = 2 * asin(sqrt(a))
 r = 6371
 return c * r * 1000
def variance(data):
 sum1 = 0
  sum2 = 0
 for i in range(len(data)):
 sum1 += data[i]
 sum2 += data[i] ** 2
 mean = sum1 / len(data)
 var = sum2 / len(data) - mean ** 2
 return var
city_neighbor = {
 "河北省": ("山西省", "内蒙古省", "辽宁省"),
 "内蒙古省": ("黑龙江省", "吉林省", "辽宁省", "河北省", "山西省", "陕西省", "宁夏省", 
"甘肃省"),
 "山西省": ("河南省", "内蒙古省", "河北省", "陕西省"),
 "四川省": ("重庆市", "云南省", "陕西省", "甘肃省", "贵州省", "西藏省", "青海省"),
 "江西省": ("浙江省", "福建省", "广东省", "湖南省", "湖北省", "安徽省"),
 "北京市": ("天津市", "河北省"),
 "贵州省": ("四川省", "重庆市", "云南省", "湖南省", "广西省"),
 "重庆市": ("四川省", "湖北市", "陕西省", "贵州省"),
 "湖南省": ("江西省", "湖北市", "重庆市", "贵州省", "广东省", "广西省"),
 "浙江省": ("江西省", "福建市", "上海市", "安徽省", "江苏省"),
}
latitudes = []
longitudes = []
provinces = []
values = []
fs = [0] * 21
ps = [0] * 21
ns = [4761] * 21
for i in range(19):
 ns[i] += 1
f = open('counter4.txt', 'r')
for i in f.readlines():
 tmp = i.strip().split(',')
 provinces.append(tmp[-1])
 latitudes.append(float(tmp[-2]))
 longitudes.append(float(tmp[-3]))
 values.append(int(tmp[2]))
graph = []
for i in range(len(provinces)):
 dis = []
 for j in range(len(provinces)):
 if (provinces[i] == provinces[j]) or (provinces[j] in
 city_neighbor[provinces[i]]):
 
dis.append(int(haversine(longitudes[i],latitudes[i],longitudes[j],latitudes[j]) / 
1000))
 else:
 dis.append(-1)
 graph.append(dis)
rounds = 10000
step = 5
while(rounds > 0):
 for i in range(len(graph)):
 ps[i] = 0
 for j in range(len(graph[i])):
 if graph[i][j] > 0:
 ps[i] = ps[i] + int(ns[j] / (graph[i][j] / 10))
 for i in range(len(fs)):
 fs[i] = values[i] / (ps[i] + ns[i])
 print("Round ", rounds, " : ", variance(fs))
 maxn = fs.index(max(fs))
 minx = fs.index(min(fs))
 ns[maxn] += step
 ns[minx] -= step
 rounds -= 1
f.close()
f = open('counter4.txt', 'r')
ff = open('counter5.txt', 'w')
index = 0
for i in f.readlines():
 ff.write(i.strip() + ',' + str(ns[index]) + '\n')
 index += 1

论文缩略图：

程序代码：

GeoPy 爬虫

# -*- coding: utf-8 -*-
import xlrd
import xlwt
import json
import requests
import numpy as np
from geopy.geocoders import Baidu
geocoder = Baidu(
 api_key='***',
 security_key='***',
 timeout=200
 )
workbook_1 = xlrd.open_workbook(r'b.xlsx')
sheet_1 = workbook_1.sheet_by_index(0)
col_1 = sheet_1.col_values(1)
col_2 = sheet_1.col_values(2)
longitudes = []
latitudes = []
for i in range(1, len(sheet_1.col_values(0))):
 longitudes.append(col_1[i])
 latitudes.append(col_2[i])
locations = []
for i in range(len(latitudes)):
 locations.append(str(latitudes[i])+','+str(longitudes[i]))
index = 0
for i in locations:
 location= geocoder.reverse(i)
 print(location.raw)
 
print(location.raw['addressComponent']['province']+","+location.raw['addressCompo
nent']['city']+","+location.raw['addressComponent']['district'])

问题一模型计算

# -*- coding: utf-8 -*-
import math
import xlrd
v_f = {"缓慢" : 200, "慢" : 400, "适中" : 800, "快" : 1000, "特快" : 1500}
v_c = {"缓慢" : 1, "慢" : 2, "适中" : 3, "快" : 4, "特快" : 5}
def get_s(s0, vm, vf, rf, p0):
 t = 0.243 + 0.128 * vf ** 2 / 8 + 0.131 * rf ** 2 / 10
 delta_r = v_f[vm] * t
 return math.pi * (math.sqrt(s0 / math.pi) + delta_r) ** 2 * p0
def get_city(s0, vm, vf, rf, p0, p1, p2):
 t = 0.243 + 0.128 * vf ** 2 / 8 + 0.131 * rf ** 2 / 10
 delta_r = v_c[vm] * t
 return s0 * p0 + delta_r / 3 * s0 * p1 + delta_r / 3 * math.sqrt(s0 / math.pi) 
* math.pi * 2 * p2
workbook_1 = xlrd.open_workbook(r'b-dealp.xlsx')
sheet_1 = workbook_1.sheet_by_index(0)
s0 = sheet_1.col_values(3)[1:]
wind = sheet_1.col_values(4)[1:]
pre_v = sheet_1.col_values(5)[1:]
diff = sheet_1.col_values(6)[1:]
prov = sheet_1.col_values(7)[1:]
fire_t = sheet_1.col_values(8)[1:]
data_input = []
for i in range(len(s0)):
 tmp = prov[i].split(',')[0]
 data_input.append([int(s0[i]), int(wind[i]), pre_v[i], int(diff[i]), 
int(fire_t[i]), tmp])
forest_value = {}
f = open('forest','r')
for i in f.readlines():
 i = i.split(' ')
 forest_value[i[0]] = float(i[1])
if __name__ == '__main__':
 countera = 0
 counterb = 0
 counterc = 0
 counterd = 0
 result = []
 for data in data_input:
 s0, vf, vm, rf, tp, pv = data
 vf = vf + 1
 if tp == 4:
 ss = get_city(s0, vm, vf, rf, 5000, 1914, 1000)
 elif tp == 3:
 ss = get_s(s0, vm, vf, rf, 15.8)
 elif tp == 2:
 ss = get_s(s0, vm, vf, rf, forest_value[pv])
 elif tp == 1:
 ss = get_s(s0, vm, vf, rf, 1.8)
 if ss < 10000000:
 countera = countera + 1
 if ss >= 10000000 and ss < 50000000:
 counterb = counterb + 1
 if ss >= 50000000 and ss < 100000000:
 counterc = counterc + 1
 if ss >= 100000000:
 counterd = counterd + 1
 if ss < 10000000:
 print("轻微火灾")
 elif ss < 50000000:
 print("较大火灾")
 elif ss < 100000000:
 print("重大火灾")
 else:
 print("特别重大火灾")
 print(int(ss / 10000))
 result.append([s0, vf, vm, rf, tp, pv, ss / 10000])
 result.sort(key = lambda enum: enum[6], reverse = True)
 for i in result[0:10]:
 print(i)
 print("轻微火灾 : ", countera)
 print("较大火灾 : ", counterb)
 print("重大火灾 : ", counterc)
 print("特别重大火灾 : ", counterd)

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可