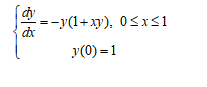计算方法(数值分析)实验：常微分方程初值问题的数值解实验 改进的Euler方法 四阶龙格库塔算法 java实现

目的要求：改进的Euler方法和四阶龙格库塔算法的计算方法原理并编程实现。要求编写实验程序（语言不限），给出实验结果。

题目：改进的欧拉法及4阶经典Runge-Kutta方法在不同步长下计算初值问题。步长分别为0.1和0.2

package com.code;

public class main {
    public static void main(String[] args){
        Eulor(0.1, 0, 1, 1);
        System.out.println();
        RungeKutta(0.1, 0, 1, 1);
    }

    public static void Eulor(double h, double left, double right, double y0){
        double yp = 0;
        double yc = 0;
        double yi = y0;
        double yi_1 = 0;
        double xi = left;
        double xi_1 = 0;
        int n;
        n = (int) ((right - left) / h);
        System.out.println("步长为" + h + "的改进的Euler方法：");
        System.out.println("   xi          yp          yc          yi+1");
        for (int i = 0; i < n; i++){
            xi_1 = xi + h;
            yp = yi + h * fx(xi, yi);
            yc = yi + h * fx(xi_1, yp);
            yi_1 = (yp + yc) / 2;

            xi = xi_1;
            System.out.printf("%-12.6f", xi);
            System.out.printf("%-12.6f", yp);
            System.out.printf("%-12.6f", yc);
            System.out.printf("%-12.6f\n", yi_1);
            yi = yi_1;
//            System.out.println("欧拉第" + i + "迭代结果为：" + yi_1);
        }


    }


    public static void RungeKutta(double h, double left, double right, double y0){
        double k1 = 0;
        double k2 = 0;
        double k3 = 0;
        double k4 = 0;

        double xi = left;
        double xi_middle = 0;
        double xi_1 = 0;

        double yi = y0;
        double yi_1 = 0;

        int n;
        int z = 0;
        n = (int) ((right - left) / h);
        System.out.println("步长为" + h + "的Runge-Kutta方法：");
        System.out.println("   xi          k1          k2          k3          k4          yi");
        for (int i = 0; i < n; i++){
            xi_1 = xi + h;
            xi_middle = xi + h / 2;
            k1 = fx(xi, yi);
            k2 = fx(xi_middle, yi + h * k1 / 2);
            k3 = fx(xi_middle, yi + h * k2 / 2);
            k4 = fx(xi_1, yi + h * k3);
            yi_1 = yi + (h / 6)*(k1 + 2 * k2 + 2* k3 + k4);
            xi = xi_1;

            System.out.printf("%-12.6f", xi);
            System.out.printf("%-12.6f", k1);
            System.out.printf("%-12.6f", k2);
            System.out.printf("%-12.6f", k3);
            System.out.printf("%-12.6f", k4);
            System.out.printf("%-12.6f\n", yi_1);

            yi = yi_1;
        }


    }

    public static double fx(double x, double y){
        return -y * (1 + x *y);
        //return 2 * x * y;
    }
}