交互式多模型算法IMM——机动目标跟踪中的应用

机动目标跟踪——交互式多模型算法IMM

原创不易，路过的各位大佬请点个赞

WX: ZB823618313

1. 对机动目标跟踪的理解

  机动目标跟踪一直是目标跟踪领域研究的难点和重点问题。建立目标运动模型和滤波算法是目标跟踪的两个重要因素。由于目标的机动具有不可预测性，使得我们很难建立精确的目标运动模型。如何建立一种有效的模型来反映目标真实的运动轨迹是高机动目标跟踪系统急需解决的问题。经过近三十年的研究，该领域取得了许多重要成果。

个人理解：机动目标跟踪拥有三要素：

1） 机动目标跟踪建模
2） 传感器测量
3） 滤波器设计

1） 机动目标跟踪建模
机动目标模型描述了目标状态随着时间变化的过程。文献[1]指出，一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后，基于状态空间的机动目标建模成为主要研究对象之一。目标的空间运动基于不同的运动轨迹和坐标系，可分为-维、二维和三维运动。而根据不同方向的运动是否相关，目标机动模型可分为坐标间不耦合模型和坐标间耦合模型。

匀速运动模型CV
匀加速运动模型CA
匀速转弯模型CT
当前统计模型CS
Singer模型
Jerk模型
…

2） 传感器测量
测量一般分为在

笛卡尔坐标系：惯导、激光雷达、ADS-B数据
极坐标/球坐标：雷达、声纳、相控阵雷达
混合坐标系：雷达+INS
大地坐标系：GPS、经纬仪、ADS-B数据
…

3） 滤波算法

  从算法层面，在目标跟踪系统中，常用的滤波算法是以卡尔曼滤波器为基本框架的估计算法。卡尔曼滤波器是一种线性、无偏、以误差均方差最小为准则的最优估计算法，它有精确的数学形式和优良的使用效能。卡尔曼滤波方法实质上是一种数据处理方法，它采用递推滤波方法，根据获取的量测数据由递推方程递推给出新的状态估计。由于计算量和存储量小，比较容易满足实时计算的要求，在工程实践中得到广泛应用。
  除此之外，非线性滤波也广泛应用与机动目标跟踪，比如：

卡尔曼滤波

非线性滤波+自适应模型
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …

自适应多模型方法
自主式多模型方法
协作式多模型方法：GPB、IMM
变结构多模型方法
… …

2. 机动目标跟踪方法概述

  机动目标跟踪是基于传感器信息对机动对象进行状态估计的过程。相应技术作为信息融合，系统的重要组成部分，在国防科技和国民经济领域有着广泛的应用。机动过程的不确定性是机动目标的主要特点，也是机动目标跟踪技术研究的重点与难点，涉及机动.目标建模、自适应滤波器设计和混杂系统多模型状态估计等理论。机动目标跟踪理论主要针对两个具有挑战性的问题:原始测量数据的不确定性问题和目标机动运动的不确定性问题。原始测量数据的不确定性来自于传感器在获取测量值的过程中，由于受到外界或自身设备本身的影响而导致的测量误差、错误等。关于这类问题的研究主要包括野值点剔除、轨迹融合等。而目标机动运动的不确定性则为机动目标的主要特点。造成目标运动的不确定性问题的原因在于实际的运动目标的机动方式具有随机性和不确定性，而作为跟踪对象的目标与跟踪者之间并无直接的信息交流，使得跟踪者无法对目标当前或即将发生的机动动作进行直接而精确的判断，因而无法直接获取目标的运动状态。

  在机动目标跟踪领域中，状态估计算法一般采用基于状态空间的动态模型。本节将就机动目标跟踪中的单模型状态估计方法进行介绍。此处的单模型方法指的是在同时刻仅采用一个模型(虽然模型可能发生切换)用于最终的状态估计。对于与实际系统匹配的线性高斯状态空间模型(模型线性，过程噪声与量测噪声分别为不相关的高斯白噪声，系统初始状态也为不相关的高斯分布)，卡尔曼滤波器是MMSE意义下的最优估计器。当目标模型满足线性高斯条件时，采用卡尔曼滤波器为状态估计通用的做法。

  由于在目标跟踪系统中，各传感器量测向量与目标被估计状态往往处于不同的坐标系中，而坐标系的转换不可避免会导致系统模型具有非线性特性。在这种情况下，需要采用相应的非线性滤波器进行状态估计。扩展卡尔曼滤波器是用得最为广泛的函数逼近类非线性滤波器。直观上说，采用扩展卡尔曼滤波器获取一次状态估计后， 在更新的状态估计值附近对原非线性函数进行重新泰勒展开，再次利用扩展卡尔曼滤波器对重新展开后的线性化函数进行估计可能获得更好的估计值。这个过程可以重复迭代进行，于是导致了迭代扩展卡尔曼滤波器。统计量過近技术中最著名的为UFP、UF具有比一阶扩展卡尔曼滤波器更小的计算量且更好的過近性能。属于随机模型逼近技术的滤波器包括中心差分滤波器、区分差分滤波器。上述滤波器均属于点估计器的范畴。而在目标跟踪中,用得较多的概率密度估计器是著名的粒子滤波器。这类滤波器是-种序贯蒙特卡洛方法，直接对非线性函数对应的概率密度函数进行逼
近。这类方法在图像跟踪领域得到了广泛的应用。

3. 交互式多模型：概述

  在现代目标跟踪系统中,对于运动模型基本不改变的运动目标,即系统的状态转移方程和观察方程都是线性的,那么在线性最小均方误差(LMMSE)的意义下,采用α-β滤波、Kal man滤波等线性滤波算法可以得到良好的滤波效果。但是对于机动目标跟踪,由于其运动状态的不确定性，效果不好。所以提出交互式多模型(IMM)的自适应机动目标跟踪算法：

  在机动目标跟踪方法中,为避免具有机动检测的跟踪算法产生的估计时间延迟和机动检测过程中跟踪性能的降低,采用基于交互式多模型(IMM)的自适应机动目标跟踪算法,通过2个目标模型的交互作用来实现对目标机动状态的自适应估计。在工程上,将基于CV和"当前"统计模型的IMM算法应用在某导航雷达跟踪系统中,经验证IMM算法对匀速直线运动、机动运动目标跟踪均能取得较好的效果。

核心思想： IMM算法的基本思想是用多个不同的运动模型匹配机动目标的不同运动模式，不同模型间的转移概率是–个马尔可夫矩阵，目标的状态估计和模型概率的更新使用卡尔曼滤波。

4. 交互式多模型：具体推导

见另一个博客

5. IMM+KF目标跟踪

WX: ZB823618313

4. IMM+UKF目标跟踪

4.1. 仿真参数

一、目标模型：CV CT CT
第一阶段：1:39s，匀速运动CV
第二阶段：40:71s，匀速圆周运动CT，角速度：$2\ast \pi /180;$
第三阶段：72:99s，匀速运动CV
第四阶段：100:131s，匀速圆周运动CT，角速度：$-3\ast \pi /180;$
第五阶段：72:99s，匀速运动CV

CV CT 模型的具体方程形式见另一个博客

二、测量模型：2D主动雷达
在二维情况下，雷达量测为距离和角度
$$\begin{gathered} r_k^m=r_k+{\tilde{r}}_k \\ {b}_k^m=b_k+{\tilde{b}}_k \end{gathered}$$
其中
$$\begin{gathered} r_k=\sqrt{(x_k-x_0{)}^{+}(y_k-y_0{)}^2)} \\ {b}_k={\tan }^{-1}\frac{y_k-y_0}{x_k-x_0} \end{gathered}$$
$[x_0,y_0]$为雷达坐标，一般情况为0。雷达量测为$z_k=[r_k,b_k{]}^{\prime }$。雷达量测方差为
$$R_k=\text{cov}(v_k)=\left[\begin{array}{cc}{\sigma }_r^2& 0\\ 0& {\sigma }_b^2\end{array}\right]$$且${\sigma }_r=120m$， ${\sigma }_b=80mrad$。

三、性能评估
RMSE(Root mean-squared error):蒙塔卡罗次数$M=500$，${\hat{x}}_{k|k}^i$为第$i$次仿真得到的估计。
$$\text{RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i)({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i{)}^{\prime }}$$
$$\text{Position RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M(x_k-{\hat{x}}_{k|k}^i{)}^2+(y_k-{\hat{y}}_{k|k}^i{)}^2}$$
$$\text{Velocity RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\dot{x}}_k-{\hat{\dot{x}}}_{k|k}^i{)}^2+({\dot{y}}_k-{\hat{\dot{y}}}_{k|k}^i{)}^2}$$
ANEES（average normalized estimation error square）,$n$ 为状态维数，${\mathbf{P}}_{k|k}^i$为第$i$次仿真滤波器输出的估计协方差
$$\text{ANEES}(\hat{x})=\frac{1}{Mn}\sum _{i=1}^M({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i{)}^{\prime }({\mathbf{P}}_{k|k}^i{)}^{-1}({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i)$$

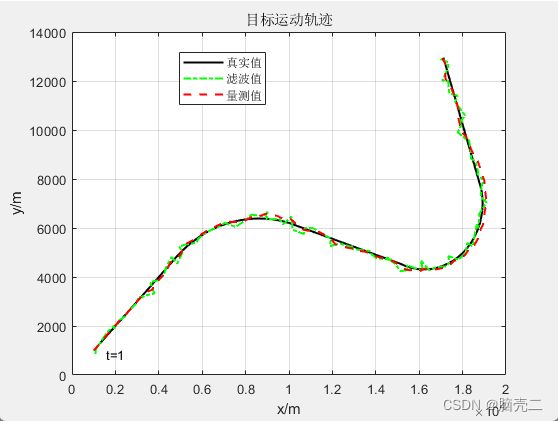
4.2. 跟踪轨迹

4.3. 位置/速度RMSE

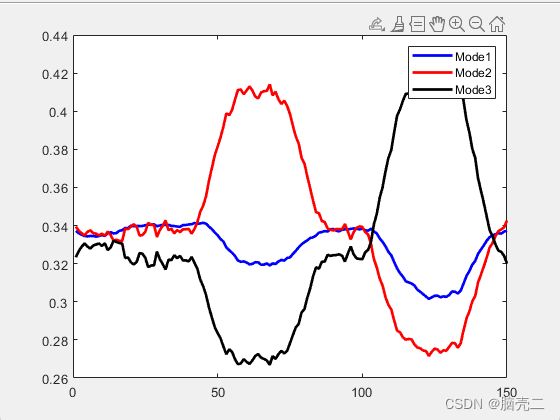
4.4. 模型概率

4.5. 部分代码

% Interacting Multiple Model2

% created by: 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 二维目标跟踪，IMM-UKF
% 目标模型：近似匀速运动模型CV 近似匀角速度运动模型CT
% 状态 x=[x位置， x速度， y位置， y速度]'
% 量测模型：三维量测(距离，角度)
% 算法: 单雷达的IMM-UKF
% 性能指标：真实轨迹，RMSE均方根误差，
% 使用三个模型进行交互，分别为CV, CT, CT


close all;
clear all;
clc;
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%系统参数设置
runs=300; %蒙特卡洛实验次数，滤波将进行100次
steps=150; %每次滤波进行80次采样

%模型1的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CV模型
T=1;
Fk1=[1 T 0 0;
    0 1 0 0;
    0 0 1 T;
    0 0 0 1;];

q1=0.01; % 目标运动学标准差，过程噪声
Qk1=q1*[T^3/3, T^2/2,        0,     0;
    T^2/2, T,            0,     0;
    0,     0,     T^3/3,   T^2/2;
    0,     0,     T^2/2,   T  ;];% 过程噪声协方差
Gk= eye(4); %过程噪声增益矩阵

%模型2的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CT模型
w1 = 2*pi/180;
Fk2=[1       sin(w1*T)/w1        0     -(1-cos(w1*T))/w1         ;
    0         cos(w1*T)        0            -sin(w1*T)        ;
    0   (1-cos(w1*T))/w1        1           sin(w1*T)/w1        ;
    0         sin(w1*T)        0             cos(w1*T)        ;];
q2 = 0.01;

Qk2= q2*[2*(w1*T-sin(w1*T))/w1^3       (1-cos(w1*T))/w1^2                    0           (w1*T-sin(w1*T))/w1^2     ;
    (1-cos(w1*T))/w1^2                     T       -(w1*T-sin(w1*T))/w1^2            0        ;
    0         -(w1*T-sin(w1*T))/w1^2       2*(w1*T-sin(w1*T))/w1^3           (1-cos(w1*T))/w1^2  ;
    (w1*T-sin(w1*T))/w1^2                     0             (1-cos(w1*T))/w1^2                         T;];

%模型3的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CT模型
w = -3*pi/180;
Fk3=[1       sin(w*T)/w        0     -(1-cos(w*T))/w         ;
    0         cos(w*T)        0            -sin(w*T)        ;
    0   (1-cos(w*T))/w        1           sin(w*T)/w        ;
    0         sin(w*T)        0             cos(w*T)        ;];
Qk3= q2*[2*(w*T-sin(w*T))/w^3       (1-cos(w*T))/w^2                    0           (w*T-sin(w*T))/w^2     ;
    (1-cos(w*T))/w^2                     T       -(w*T-sin(w*T))/w^2            0        ;
    0         -(w*T-sin(w*T))/w^2       2*(w*T-sin(w*T))/w^3           (1-cos(w*T))/w^2  ;
    (w*T-sin(w*T))/w^2                     0             (1-cos(w*T))/w^2                         T;];



%量测方程参数设置，Zk=H*Xk+Vk
v_mu=[0,0]';
% 雷达传感器标准差，即测量噪声
sigma_r=200; sigma_b=0.3*pi/180;%雷达1
% 雷达坐标
xp(:,1)=[20000, 0, 3 ,0 ]; %第1个传感器的位置，可设置[x坐标， 0， y坐标， 0]，xy对应传感器二维位置中间的0不能变，只是为了适应维数

%滤波初始化设置
X_aver_zero=[30000,80,20000,50]';
P_zero=diag([1e6,1e3,1e6,1e3]);

%模型概率初始化
m=[0.8;0.1;0.1];
%模型转移概率
Pa=[0.8 0.1 0.1;
    0.1 0.8 0.1;
    0.1 0.1 0.8;];

%误差存储
X_true=zeros(4,steps,runs);
Z_true=zeros(2,steps,runs);
X_err_IMM=zeros(4,steps,runs);
X_IMM=zeros(4,steps,runs);
PI=zeros(3,steps,runs);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


randn('state',sum(100*clock));  %每次给不同的状态重置随机数产生器（因为clock每次都不同）

%%

for index=1:runs %蒙特卡洛次数
    index         %显示运行次数
    
    %滤波初始化
    X=X_aver_zero+sqrtm(P_zero)*randn(4,1);%产生真实X0
 %三个滤波器的初始化   
    xk_UKF1=X_aver_zero;             %X(0|0)= X_aver_zero
    Pk_UKF1=P_zero;                  %P(0|0)= P_zero
    xk_UKF2=X_aver_zero;
    Pk_UKF2=P_zero;
    xk_UKF3=X_aver_zero;
    Pk_UKF3=P_zero;
    
    
    %% 产生真实轨迹
    for k=1:39
        X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);     %产生真实轨迹
        X_true(:,k,index)=X;
    end
    for k=40:71
        X=Fk2*X+Gk*sqrtm(Qk2)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=72:99
        X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=100:131
        X=Fk3*X+Gk*sqrtm(Qk3)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=132:steps
        X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);
        X_true(:,k,index)=X;
    end
    
    %% 状态递归实现
    for k=1:steps

原创不易，路过的各位大佬请点个赞