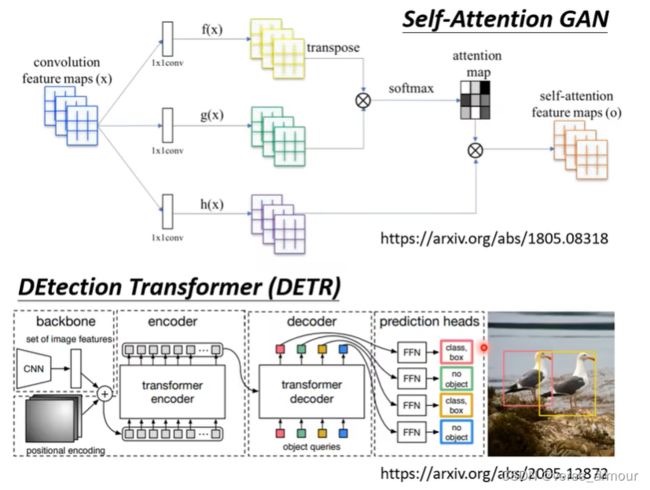
transformer:self-attention,muti-head attention,positional encoding

transformer和RNN、LSTM相比

RNN需要$t_0$时刻的数据才能计算出$t_1$时刻的数据，无法并行化计算，只具有短期记忆。
而transformer理论上的记忆长度是不受限制的，并且可以并行化计算。
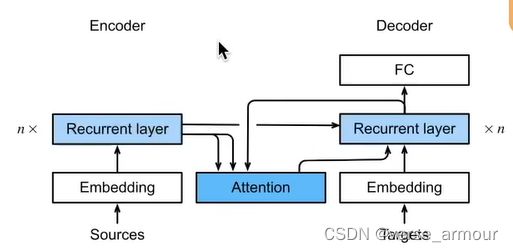
transformer基于编码器-解码器来处理序列对，跟使用注意力的seq2seq不同，transformer纯基于注意力。

seq2seq

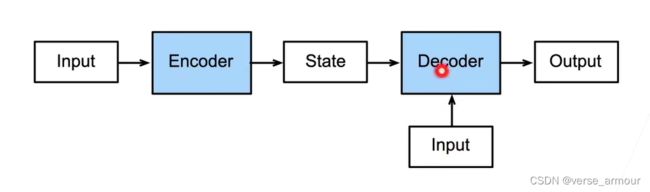
编码器-解码器架构

一个模型可以分成两块：

• encoder，处理输入；
• decoder，生成输出，有的时候也可以处理输入。

• CNN
  
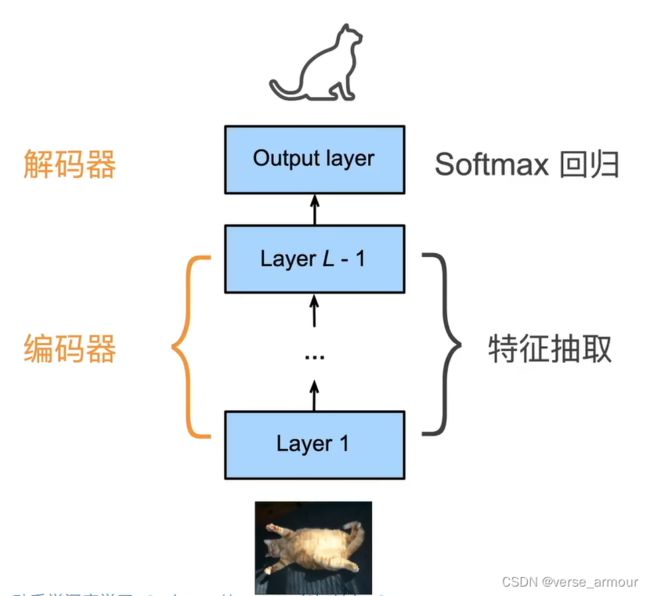
  对于CNN来说，中间的特征提取层（中间表达式）可以抽象成一个编码器；softmax回归进行分类标号可以抽象成一个解码器。
• RNN
  
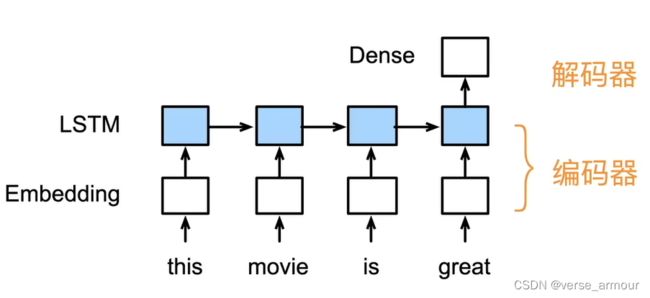
  RNN同理，最后一个时刻隐藏层的输出是编码器编码的结果，最后再通过全连接层进行解码。
• 编码器解码器API

from torch import nn

#@save
class Encoder(nn.Module):
    """编码器-解码器架构的基本编码器接口"""
    def __init__(self, **kwargs):
        super(Encoder, self).__init__(**kwargs)

    def forward(self, X, *args):
        raise NotImplementedError

#@save
class Decoder(nn.Module):
    """编码器-解码器架构的基本解码器接口"""
    def __init__(self, **kwargs):
        super(Decoder, self).__init__(**kwargs)

    def init_state(self, enc_outputs, *args):
        raise NotImplementedError

    def forward(self, X, state):
        raise NotImplementedError

#@save
class EncoderDecoder(nn.Module):
    """编码器-解码器架构的基类"""
    def __init__(self, encoder, decoder, **kwargs):
        super(EncoderDecoder, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, enc_X, dec_X, *args):
        enc_outputs = self.encoder(enc_X, *args)
        dec_state = self.decoder.init_state(enc_outputs, *args)
        return self.decoder(dec_X, dec_state)

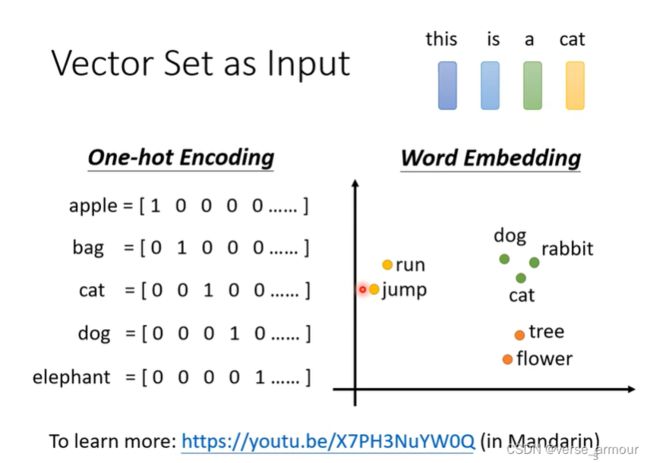
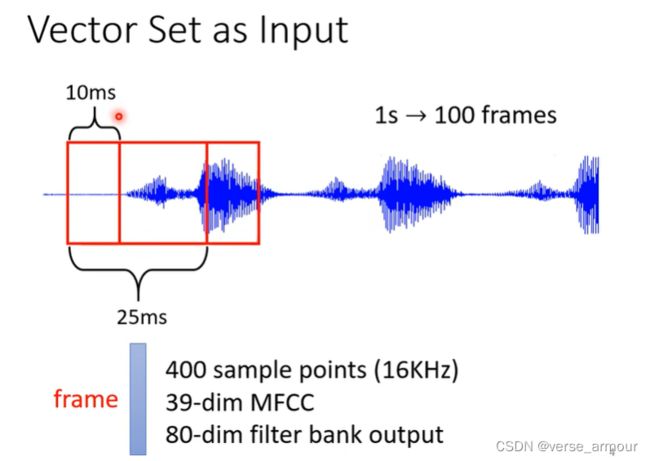
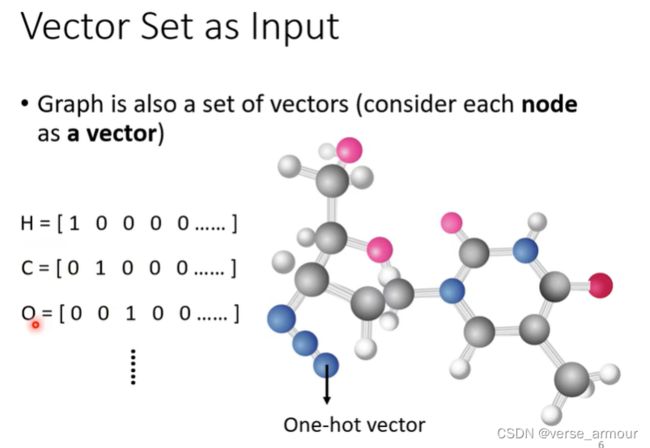
What is Input?

• sentence
• voice
• graph
  

给每个单词一个向量

• One-hot Encoding
• Word Embedding(包含了每个单词的语义信息)
  一个句子就是一排长度不一的向量

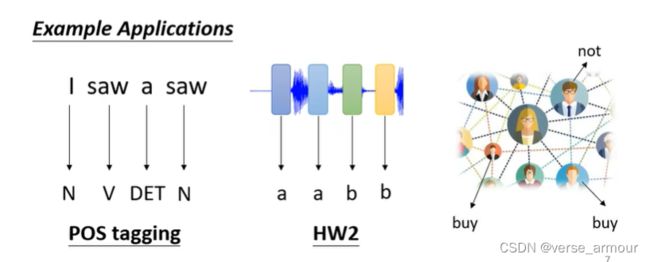
What is Output?

• N-N:each vector has a label
  
• N-1:the whole sequence has a label

• N-N’(seq2seq):model decides the number of labels itself
  比如机器翻译、语音识别。输入和输出的数量不一样。

N-N:each vector has a label

为什么出现了self-attention机制？因为如果将输入sequence中每个足够大的向量（因为我们的输入需要统一长度）放进去训练会产生巨大的参数量，不利于我们的训练。因此我们采用一种自注意力机制来对输入sequence的每个向量进行self-attention处理，考虑输入sequence中每个向量和其他输入向量之间的关系。

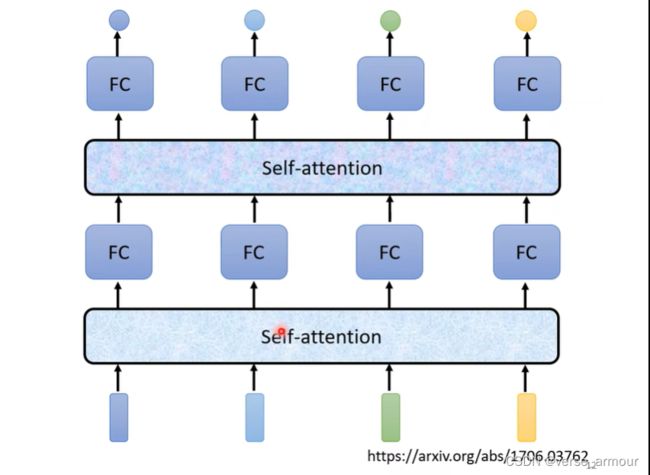
（1）整体结构

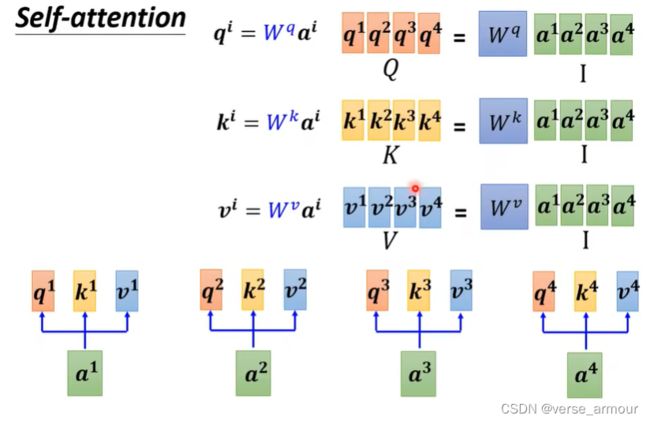
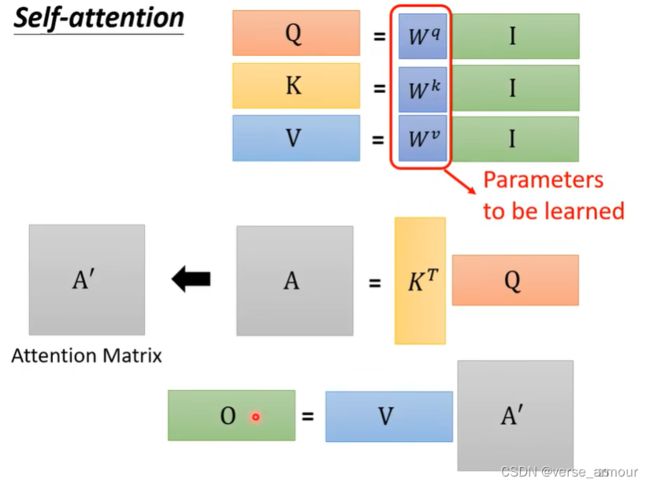
（2）如何实现self-attention模块

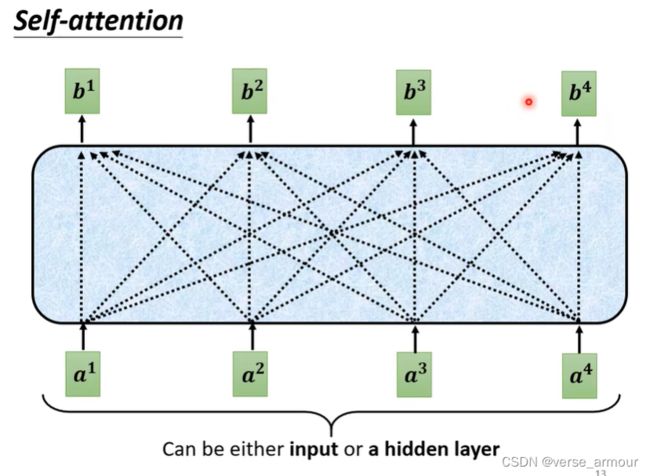
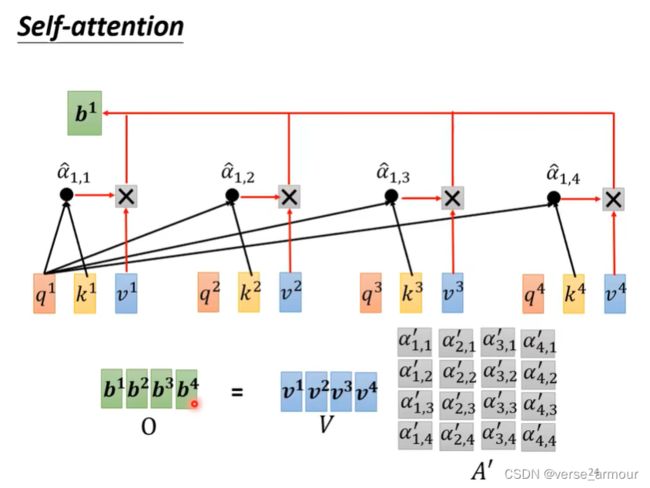
每个b向量都是考虑过输入sequence中所有的a向量才输出的。
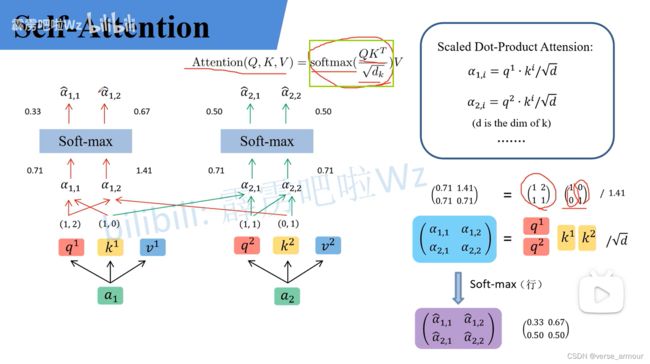
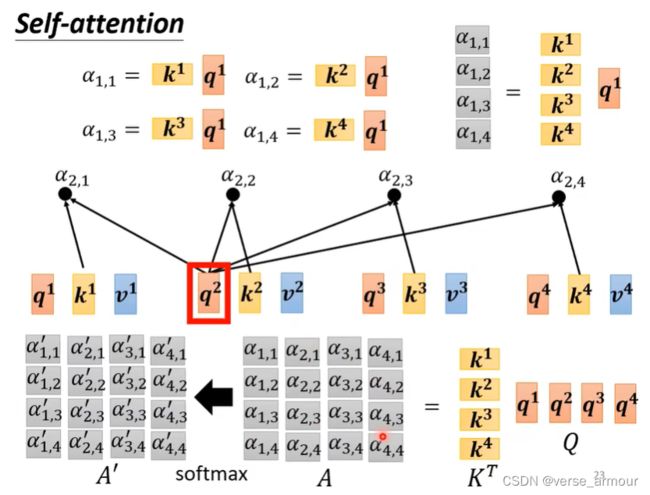
如何计算出两个向量之间的相关性呢？
一般有两种方法：dot-product和additive
一般情况下我们使用的都是dot-product。

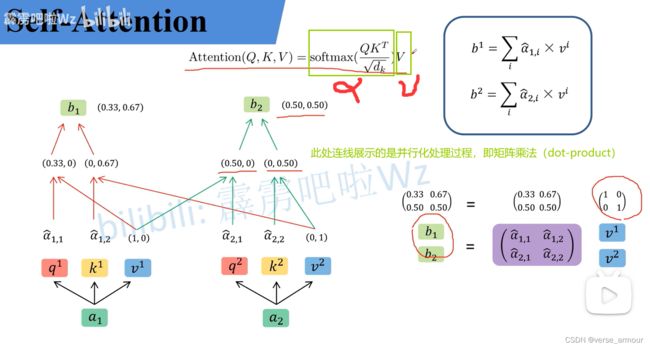
将以上过程封装成一个Self-Attention Layer，即最终transformer模型中的一个小模块。
输入$a_1,a_2$，输出$b_1,b_2$。

（3）从矩阵乘法的角度理解self-attention

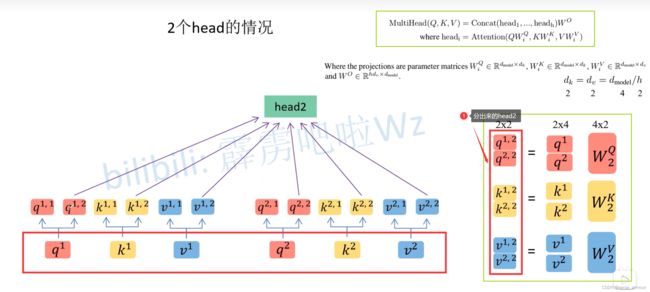
（4）Muti-head Self-attention（多头注意力模块）

• head1
  

• head2
  

用一个大矩阵生成QKV之后拆分成多个头，和用多个小矩阵，每个头生成一个$Q_i、K_i、V_i$，在数学上是完全等效的，因此多头自注意力机制就是采用相同结构，不同的参数，把自注意力机制重复n次

此处的$W^o$是可训练参数。

muti-head的操作类似于group convolution（组卷积）

将以上过程封装成一个Muti-Head Attention Layer，即最终transformer模型中的一个小模块。

（5）Positional Encoding:位置编码为自注意力机制赋能

如上图所示，如果交换$a_2,a_3$的位置，是不影响$b_1$的输出的。这显然是不合理的。
所以我们引出位置编码的概念。

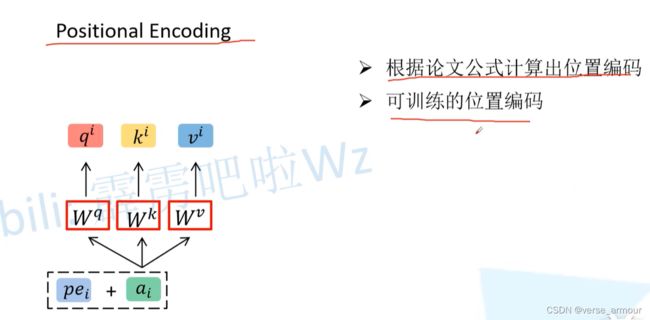
这里的P就是我们所说的位置编码信息positional encoding。

self-attention在语音上的应用：

self-attention在视觉上的应用：
图像可以看成是vector set。