第一章 UCI数据集wine.data主成分分析PCA

---

前言

学习数据挖掘，用于记录练习和回顾

---

一、什么是PCA？

经典主成分分析（Classical Principal Component Analysis）的核心思想：PCA的思想是将n维特征映射到k维上（k

---

二、PCA算法流程

1.按列计算数据集X的均值Xmean，然后令Xnew=X−Xmean
2. 求解矩阵Xnew的协方差矩阵，并将其记为Cov
3.计算协方差矩阵Cov的特征值和相应的特征向量
4.将特征值按照从大到小的排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵Wnxk
5. 计算XnewW，即将数据集Xnew投影到选取的特征向量上，这样就得到了我们需要的已经降维的数据集XnewW

---

二、使用步骤

1.引入库

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt

2.读入数据

代码如下（示例）：

df_wine = pd.read_csv('./UCI/wine/wine.data', header=None) # 加载葡萄酒数据集
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values # 把分类属性与常规属性分开
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.3, random_state=0) # 把整个数据集的70%分为训练集，30%为测试集

3.数据标准化（规范化）

如果数据特征在不同的范围上，要先对数据集标准化。下面3行代码把数据集标准化为均值0方差1,避免异常值对结果造成影响

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)

4.主成分分析PCA

#计算协方差矩阵
cov_mat = np.cov(X_train_std.T)

#求协方差矩阵的特征值和特征向量
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
# 下面的输出为eigen_vals
"""求出的特征值的意义就是特征向量的大小，因此只要找出最大特征值所对应的特征向量就可以知道哪个方向保留的方差最大。"""
# array([ 4.8923083 ,  2.46635032,  1.42809973,  1.01233462,  0.84906459,
#         0.60181514,  0.52251546,  0.08414846,  0.33051429,  0.29595018,
#         0.16831254,  0.21432212,  0.2399553 ])


"""
下面的代码都是绘图的，涉及的参数建议去查看官方文档
计算统计主成分分析
"""

tot = sum(eigen_vals) # 求出特征值的和
"""即每个主成分捕捉多少方差,描述样本的贡献值"""
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)] # 求出每个特征值占的比例（降序）

plt.bar(range(len(eigen_vals)), var_exp, width=1.0, bottom=0.0, alpha=1, label='individual explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.show()

第一个主成分将近0.4，第二个主成分将近0.2，也就是说明前两个主成分可以捕捉该数据集60%的方差；第三个主成分0.1，前三个主成分可以捕捉70%

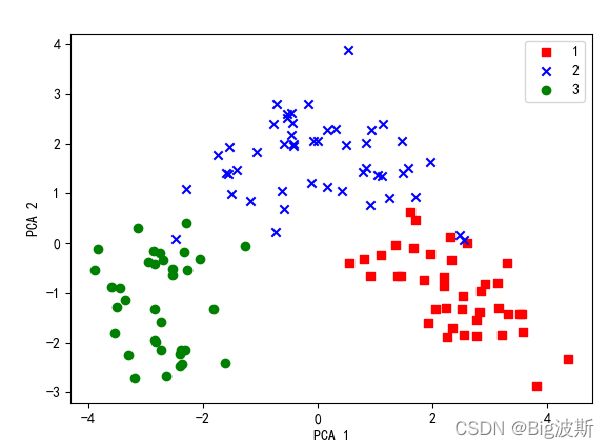
5.PCA可视化

选取前两个主成分和前三个主成分分别做二维和三维分布图

eigen_pairs =[(np.abs(eigen_vals[i]),eigen_vecs[:,i]) for i in range(len(eigen_vals))] # 把特征值和对应的特征向量组成对
eigen_pairs.sort(reverse=True) # 用特征值排序

"""选出前2对来构建映射矩阵，但是在实际应用中，应该权衡计算效率和分类器之间的性能来选择恰当的主成分数量"""
first = eigen_pairs[0][1]
second = eigen_pairs[1][1]
third = eigen_pairs[2][1]
first = first[:,np.newaxis]
second = second[:,np.newaxis]
third = third[:,np.newaxis]

w = np.hstack((first,second,third))



plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
X_train_pca = X_train_std.dot(w) # 转换训练集
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(X_train_pca[y_train==l, 0], X_train_pca[y_train==l, 1], c=c, label=l, marker=m) # 散点图
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.legend(loc='upper right')
# plt.show()


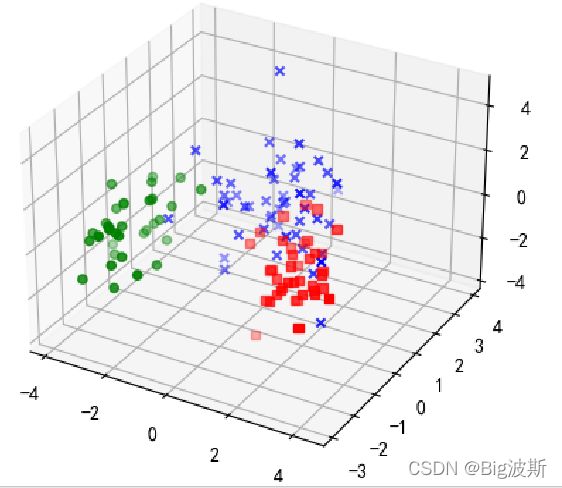
"""3d展示主成分"""
fig =plt.figure()
ax = fig.add_subplot(111,projection='3d')
for l, c, m in zip(np.unique(y_train), colors, markers):
    ax.scatter(X_train_pca[y_train==l, 0], X_train_pca[y_train==l, 1],X_train_pca[y_train==l, 2], c=c, label=l, marker=m)
plt.show()

---

总结（拓展）

参考文章 ：Blessy_Zhu https://blog.csdn.net/weixin_42555080