第二章 wine数据集几种可视化集合

---

前言

学习数据挖掘，用于记录练习和回顾

---

一、wine红酒质量数据集

数据地址：https://archive.ics.uci.edu/ml/datasets/Wine+Quality

二、使用步骤

1.引入库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from math import exp

2.读入数据

df = pd.read_csv('./UCI/wine_quality/winequality-red.csv',sep = ';')
print(df.head())
df.info()
df.describe()

# 获取所有的自带样式
print(plt.style.available)
#  使用plt自带的样式美化
plt.style.use('ggplot') #柱形图
#plt.style.use('seaborn-poster') #箱型图用这个

---

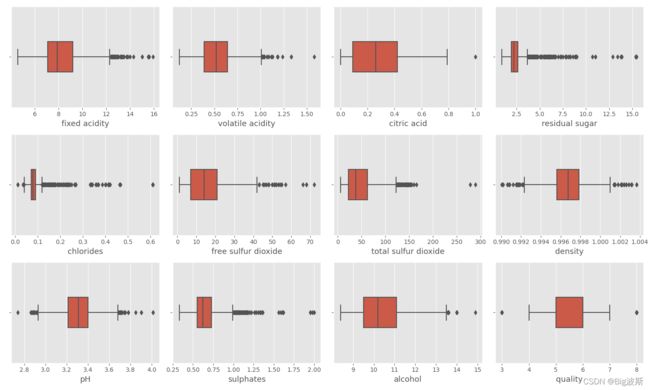
3.绘制箱线图

#  获取每个字段
colnm = df.columns.to_list()
print(colnm)
print(len(colnm))
# 颜色
color = sns.color_palette()
fig = plt.figure(figsize=(15,9))
for i in range(12):
    plt.subplot(3,4,i+1)  # 三行四列 位置是i+1的子图
    # orient："v"|"h" 用于控制图像使水平还是竖直显示（这通常是从输入变量的dtype推断出来的，此参数一般当不传入x、y，只传入data的时候使用）
    sns.boxplot(df[colnm[i]], orient="v", width = 0.3, color = color[0])
    plt.xlabel(colnm[i],fontsize = 13)
    #plt.xlabel('one_pic')
#  图形调整
plt.subplots_adjust(left=0.2, wspace=0.8, top=0.9, hspace=0.1)  #  子图的左侧 子图之间的宽度间隔   子图的高   子图之间的高度间隔
# tight_layout会自动调整子图参数，使之填充整个图像区域
plt.tight_layout()
plt.savefig('箱型图')

---

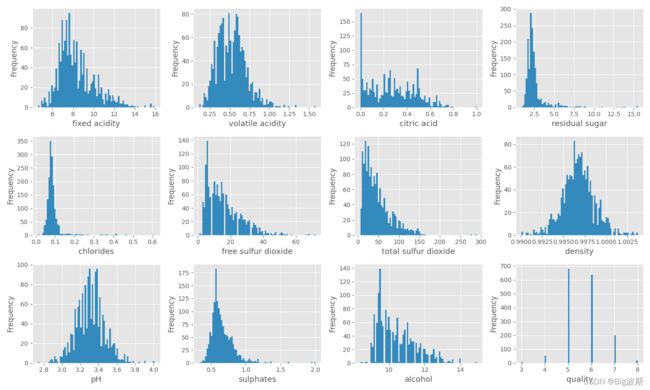
4.绘制直方图

fig = plt.figure(figsize=(15, 9))
for i in range(12):
    plt.subplot(3,4,i+1)  # 3行4列 位置是i+1的子图
    df[colnm[i]].hist(bins=80, color=color[1])  # bins 指定显示多少竖条
    plt.xlabel(colnm[i], fontsize=13)
    plt.ylabel('Frequency')
# tight_layout会自动调整子图参数，使之填充整个图像区域
plt.tight_layout()
plt.savefig('直方图')

---

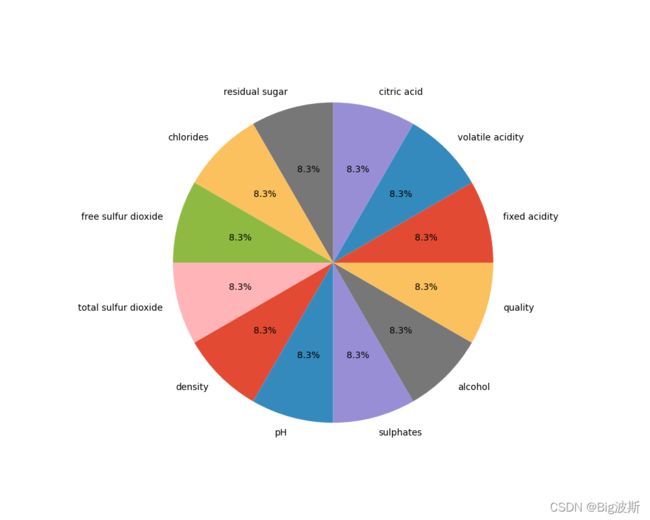
5.绘制饼图

plt.figure(figsize = (10,8))
#第一个参数是扇形的面积
#labels参数为扇形的说明文字
#autopct参数为扇形占比的显示格式
plt.pie([len(df[label]) for label in colnm] ,labels=colnm,autopct='%1.1f%%')
plt.savefig('饼图')

---

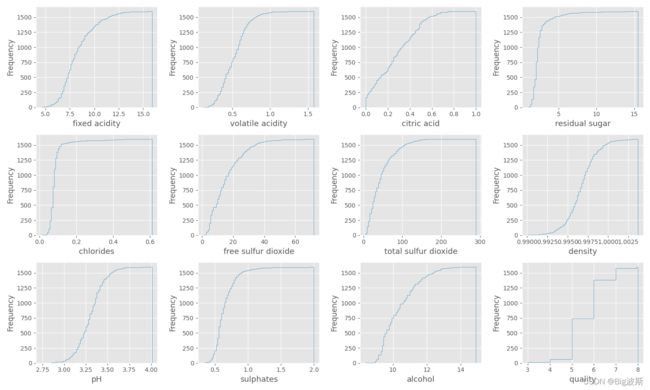
6.绘制累积曲线

fig = plt.figure(figsize=(15, 9))
#创建累积曲线
#第一个参数为待绘制的定量数据
#第二个参数为划分的区间个数
#normal参数为是否无量纲化
#histtype参数为‘step’，绘制阶梯状的曲线
#cumulative参数为是否累积
for i in range(12):
    plt.subplot(3,4,i+1)  # 3行4列 位置是i+1的子图
    df[colnm[i]].hist(bins=80, color=color[1],histtype='step',cumulative=True)  # bins 指定显示多少竖条
    plt.xlabel(colnm[i], fontsize=13)
    plt.ylabel('Frequency')
# tight_layout会自动调整子图参数，使之填充整个图像区域
plt.tight_layout()
plt.savefig('累积曲线图')

---

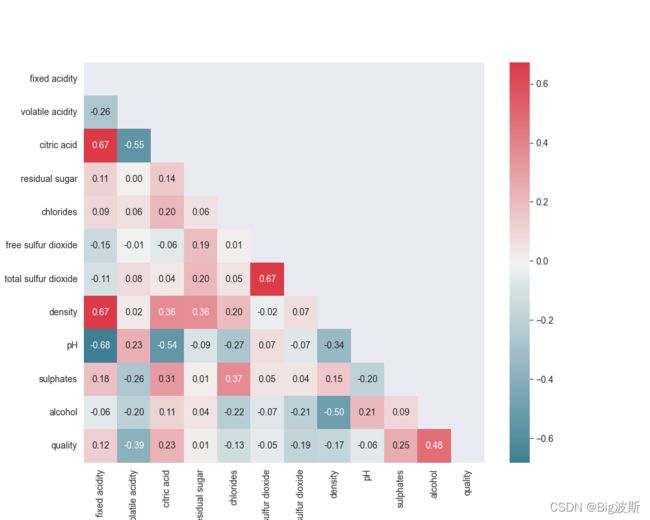
7.绘制热力图

sns.set_style("dark")
plt.figure(figsize = (10,8))
#colnm = df.columns.to_list()[:11] + ['total acid', 'quality']
# 不满足连续数据，正态分布，线性关系，用spearman相关系数是最恰,当两个定序测量数据之间也用spearman相关系数
# pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，即针对线性数据的相关系数计算，针对非线性数据便会有误差。
# kendall：用于反映分类变量相关性的指标，即针对无序序列的相关系数，非正太分布的数据
# spearman：非线性的，非正太分析的数据的相关系数
# mcorr = df[colnm].corr(method='spearman')

#  如果不是数字   get_dummies   one_hot 编码之后 计算相关系数
mcorr = df[colnm].corr()
# zeros_like函数主要是想实现构造一个矩阵W_update，其维度与矩阵W一致，并为其初始化为全0；这个函数方便的构造了新矩阵，无需参数指定shape大小
# mask = np.zeros_like(mcorr, dtype=None)   #  0 0 0 0
mask = np.zeros_like(mcorr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True   # 1
# 调色盘 对图表整体颜色、比例进行风格设置，包括颜色色板等  调用系统风格进行数据可视化
cmap = sns.diverging_palette(220, 10, as_cmap=True)
#  热力图
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')
plt.savefig('热力图')

---

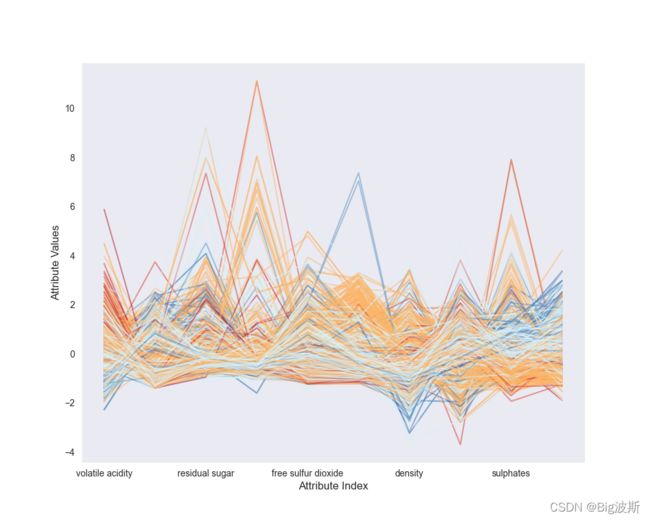
8.绘制平行坐标图

plt.figure(figsize = (10,8))
##归一化
wineNormalized = df
summary = df.describe()
nrows = len(df.index)
ncols = len(wineNormalized.columns)
nDataCol = len(df.columns) -1
for i in range(ncols):
    mean = summary.iloc[1, i]
    sd = summary.iloc[2, i]
    wineNormalized.iloc[:, i:(i + 1)] = (wineNormalized.iloc[:, i:(i + 1)] - mean) / sd
for i in range(nrows):
    # plot rows of data as if they were series data
    dataRow = wineNormalized.iloc[i, 1:nDataCol]
    normTarget = wineNormalized.iloc[i, nDataCol]
    labelColor = 1.0 / (1.0 + exp(-normTarget))
    dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.savefig('平行坐标图')

可以调节属性顺序让曲线分离的更直观

---

9.绘制等高线图

step = 10
x = np.arange(0,200,step)
y = np.arange(0,200,step)
#也可以用x = np.linspace(-10,10,100)表示从-10到10，分100份
#将原始数据变成网格数据形式
X,Y = np.meshgrid(x,y)
#写入函数，z是大写
Z = X**2+Y**2
#设置打开画布大小,长10，宽6
plt.figure(figsize=(10,6))
#填充颜色，f即filled
plt.contourf(X,Y,Z)
#画等高线
plt.contour(X,Y,Z)

plt.show()

---

总结

切尔诺夫脸图可以用matlab实现，但是使用python方法暂时没找到相关matlab包