相关分析与回归分析
相关与回归分析就是了解变量之间相关关系的统计方法
一.相关分析
具有相关关系的变量之间,如果不区分原因和结果,我们称之为相关分析
相关分析是看两个因素之间的相关性,不需要确定哪个是自变量,哪个是因变量,两个因素是平行关系
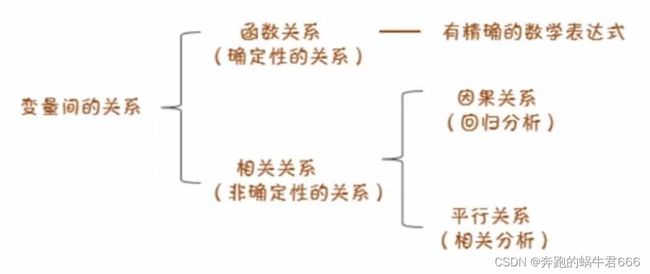
1.变量之间的关系
2.函数关系
定义:当一个变量取一个值的时候,另一个变量有确定值与之对应
特点:变量之间是一一对应的确定关系;Y随X一起变化,并完全依赖于X;各观测点落在一条线上
3.相关关系
定义:变量之间保持着不确定性的数量依存关系,即变量间的关系不能用函数关系精确的表达
特点:一个变量的取值不能由另一个变量唯一确定;当变量X取某个值时,变量Y的取值可能有好几个;各观测点分布在直线周围
两个变量之间存在相关关系,并不一定意味着一个变量会影响到另一个变量,也不意味着两者存在实际关系,即数学关系 ≠ 实际关系
4.类型
正线性相关:一个变量增长,另一个变量也相应的增长
负线性相关:一个变量增长,另一个变量也相应的减少
不相关:两个变量之间是随机模式,不存在相关性
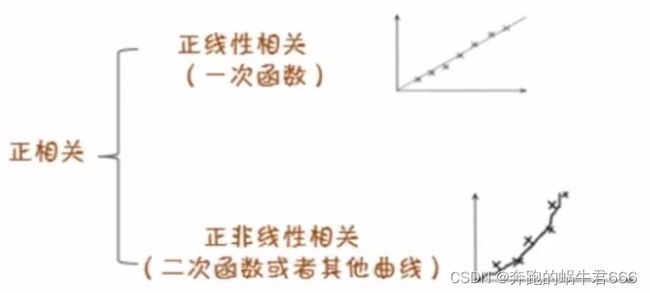
正相关不一定是正线性相关,还要看变量之间具体的函数F(x)是一次函数,还是二次函数或者其它曲线
如果是一次函数叫正线性相关,如果不是一次函数,就只能说两者是正相关,不能说正线性相关
区别是线性还是非线性,主要看函数y = F(x)对自变量x的依赖关系
线性相关的函数是一次函数,是正比例关系或者反比例关系,函数一般为y = Ax + B,其图像表现为一条直线
非线性相关的函数关系不是一次函数,图像不是直线,一般情况是曲线或抛物线关系
二.回归分析
具有相关关系的变量之间,如果存在因果关系,我们用回归分析来确定它们之间的关系
因果关系的表现形式
①一种原因引起一种结果
②多种原因引起一种结果
③变量之间互为因果
1.相关分析与回归分析的关系
①相关分析强调的是现象之间是否相关,相关的方向和密切程度,而回归分析则要分析现象之间的具体形式,确定其因果关系,并用数学模型来表现其具体关系
②在研究相关分析时,不需要区分自变量和因变量,但回归分析的首要问题就是确定哪个是自变量,哪个是因变量
③现象之间相关分析的研究,只能计算一个相关系数;而回归分析时回归系数可能有两个,也就是两现象互为因果关系时,可以确定两个独立回归方程,从而就有两个不同的回归系数
总结:相关分析是回归分析的基础和前提,只有变量之间存在高度相关时,进行回归分析确定相关的具体形式才有意义;回归分析是相关分析的继续和深入,变量之间的相关程度需要回归分析来确认
2.求最佳拟合线步骤
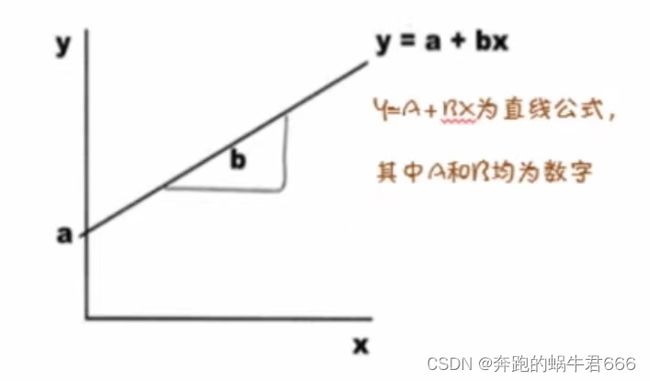
①求出直线公式
②将误差最小化
③求误差平方和
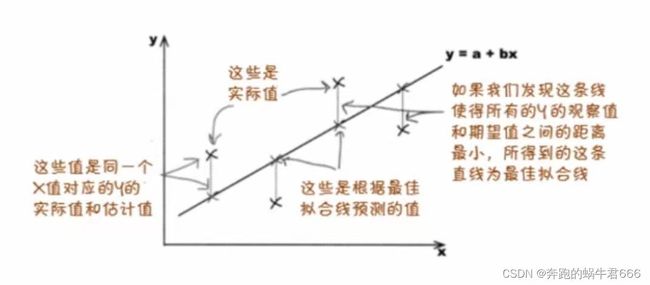
所以,求最佳拟合线就是求使得误差平方和最小的那条直线
3.相关系数
对于直线y = A +Bx,尽管名为“最佳拟合线”,但我们并不知道这条线的准确性如何,还有一件事需要考虑,回归线的相关性强度
尽管最佳拟合线是与数据拟合程度最高的直线,但它并不能与每个点都精确拟合
让我们查看一些相关关系,看看直线和数据的拟合情况
①精确线性相关
直线和每个点几乎精确拟合
可以这样说,依据这条线做出的任何预测可能都是准确的
②非线性相关
这一组数据未体现出线性相关性
你可以用最小二乘回归法算出一条回归线,但据此做出的任何预测都不太可能准确
两组数据都有回归线,但数据的实际拟合程度却不大相同,第一组数据的相关性十分明显,但第二组数据十分分散,以致回归线丧失了应有的作用
有一种方法可用于衡量直线拟合的程度:计算相关系数
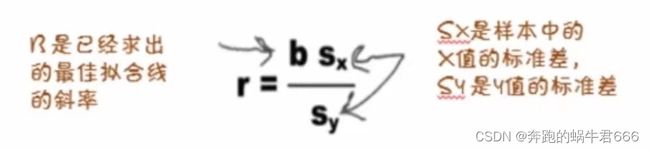
相关系数是介于-1和1之间的一个数,描述了各个数据点与直线的偏离程度,通过它可以量度回归线与数据的拟合度,通常用字母R来表示
通常情况下,R介于[-1,1]之间,R越接近1或-1,相关性越强,数据点距离直线越近,拟合准确度越高;R越接近0,相关性越弱,数据点距离直线越远,甚至不存在相关关系
回归分析又称为曲线拟合,其本质就是一个函数估计的问题,即找出因变量和自变量之间的函数关系(因果关系)