混淆矩阵、精确率、召回率、F1值、ROC曲线、AUC曲线

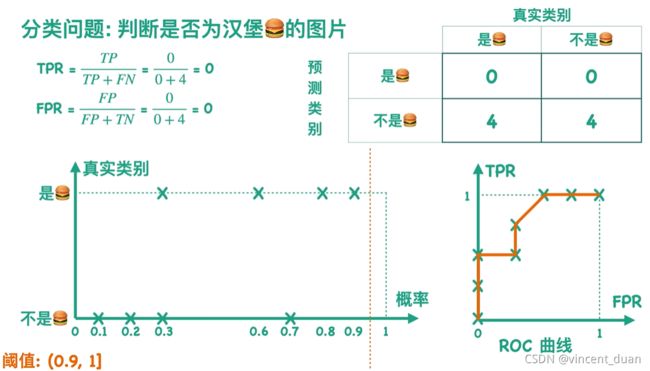
假设一个分类器A，分类器A的作用是告诉你一张图片是不是汉堡，我们如果想知道这个分类器的效果到底好不好，如何做？

最简单的方法就是将手机里所有的图片都扔给分类器A看，让分类器告诉我们哪些是汉堡

我们无法直观的看到这个分类器的效果怎么样，有没有一种更好地办法来直观而又不损失信息的表示它的实验结果。

一张图片的真实类别有两种情况（是汉堡，不是汉堡），分类器的预测类别也可以告诉我们两种情况（是汉堡，不是汉堡）。所以得到下面这张图，这张图就是混淆矩阵（Confusion Matrix）：

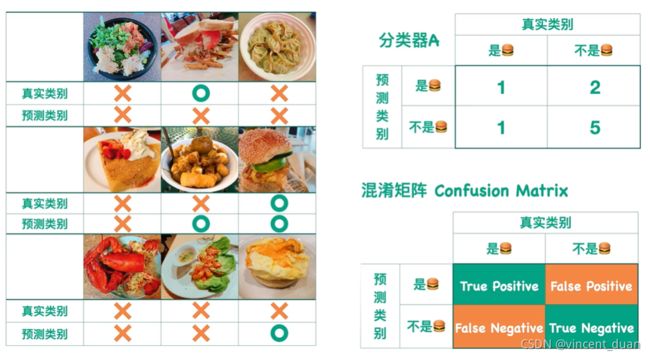
根据混淆矩阵，我们看到薄荷绿的区域是我们预测正确的区域，因此分别叫做True Positive和True Negative，而橙色的部分我们预测错了，因此我们叫做False Positive和False Negative，第一行我们分类器预测成了positive类，所以第一行第二个单词是positive，同理第二行第二个单词是Negative。

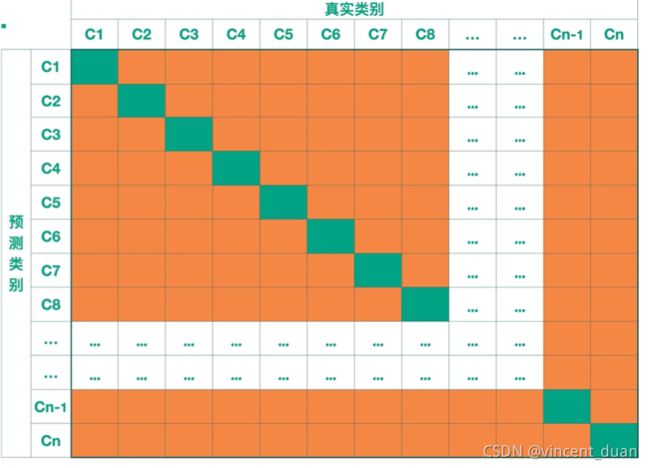
上面形成的$2\times 2$的矩阵是对于二分类问题来说的，如果我们是多分类问题，如何表示，我们的真实类别变成了多分类，预测类别也变为多分类：

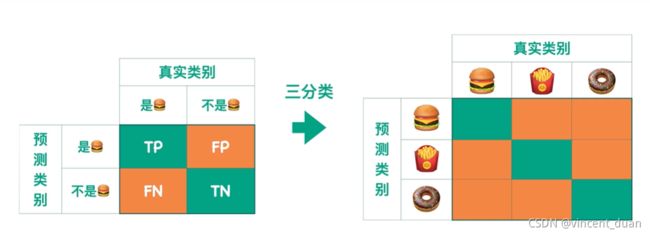
从左上角到右下角的对角线，也就是薄荷绿的区域表示模型预测正确的情况区域，而剩下的橙色部分表示分类器预测错误的情况下的。

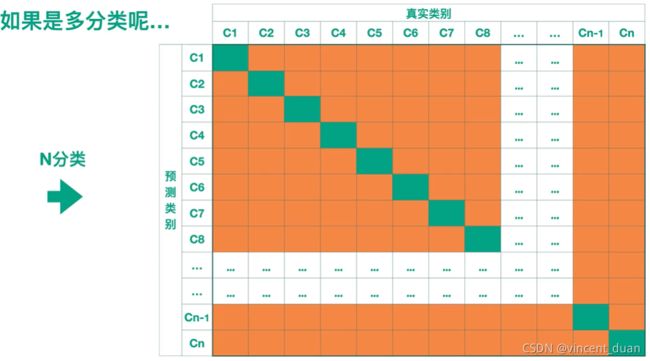
如果是对于N分类的问题，那么会形成$n\times n$的矩阵，薄荷绿的部分就是分类器预测正确的部分，橙色的部分表示预测错误的部分，所以我们希望我们的分类器在薄荷绿的部分数值越大越好，橙色部分数值越小越好。

准确率、精确率、召回率、F1值

假设有两个分类器，分类器A和分类器B，他们的作用是判断一张图片是不是汉堡，给出下面的混淆矩阵：

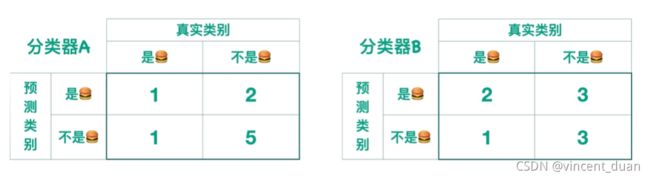
我们想知道分类器A的效果好还是分类器B的效果好？有没有什么评估指标？

分类器到底分对了多少？

• 准确率（accuracy）：真实类别与预测类别相同的数值求和，除以总体样本。例如分类器A的准确率是$\frac{1+5}{1+2+1+5}=0.67$。
• 精确率（precision）：换一个角度考虑，假设我们有一个图片搜索引擎，当我输入汉堡时，他能返回所有汉堡图片，那么我关心的问题是返回的图片里正确的有多少。例如分类器A的精确率是：$\frac{1}{1+2}=0.33$，也就是说返回的正确的汉堡图片，除以返回的所有的图片数目。精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了，一种就是把正类预测为正类(TP)，另一种就是把负类预测为正类(FP)，也就是$precision=\frac{TP}{TP+FP}$
• 召回率（recall）：有多少张应该返回的图片，但是分类器却没有找到，用返回图片的汉堡的数目除以样本中所有样本的数目，例如分类器A的召回率是：$\frac{1}{1+1}=0.5$。召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN)。也就是$recall=\frac{TP}{TP+FN}$

精确率和召回率在某种程度上呈现一种此消彼长的状态，举一个极端的情况，假设要搜索出汉堡的图片，分类器返回了图片库中所有的样本，这时的召回率一定是100%，但是精确率却非常低，因为精确率的分母是样本总数，所以我们不能一味地要求召回率高或者精确率高，因为会导致另一个指标相对较低，这时我们提出一个新的指标F1值。

$F_1$值是$F_{\beta }$值的一个特殊情况：

当我们认为精确率和召回率的重要程度是同等重要，那么$\beta =1$就是$F_1$值了。

但是在某些问题下，我们会认为召回率更重要或者精确率更重要，在医疗领域我们不希望任何患者被遗漏，所以召回率更重要，这时往往将$\beta =2$。在另外一些领域我们认为精确率更重要，我们会将$\beta$取一个0到1的值。

在多分类情况下，某一类的准确率就是图中对应薄荷绿对应的数值，除以所有的数值；某一类的精确率是对应薄荷绿的区域数值，除以预测类别行的所有数值求和；某一类的召回率是对应的薄荷绿的区域数值，除以真实类别列的所有数值求和；F1值就是精确率和召回率的调和平均。这样就可以把每一类都求出精确率、召回率以及F1值。这就是微观micro-情况

micro f1不需要区分类别，直接使用总体样本的准确率和召回率，计算f1 score。

如果我们想知道整个模型的精确率、召回率和F1值怎么求？我们可以做一个加权平均，权重的方式可以根据测试样本中每一类样本的数目来定。这就是宏观macro-的情况。

不同于micro f1，macro f1需要先计算出每一个类别的准确率和召回率及其f1 score，然后通过求均值得到在整个样本上的f1 score。

ROC曲线、AUC值

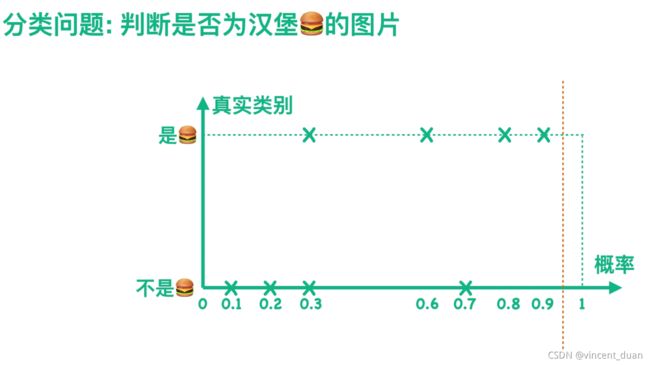
假设我们有一个分类器，可以判断一张图片是不是汉堡，实际上我们的分类器会计算得到一张图片属于汉堡的概率，进而对图片的类别进行预测是汉堡或者不是汉堡。

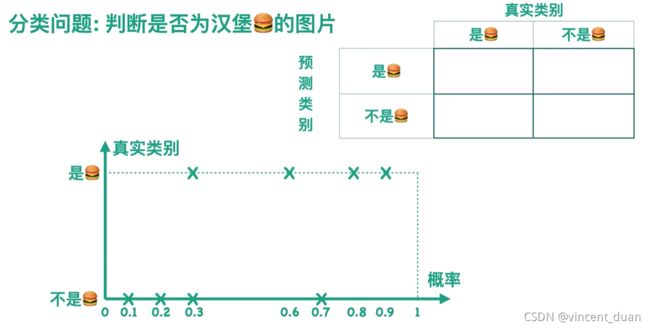
假设我们的阈值设为0.5，当概率大于等于0.5时，分类器认为这张图是汉堡，也就是下图中虚线右边的部分，我们用橙色来表示；当概率小于0.5时，分类器认为这张图片不是汉堡，也就是图中虚线左边的部分，我们用薄荷绿来表示，我们可以根据预测结果得到混淆矩阵，如下图：


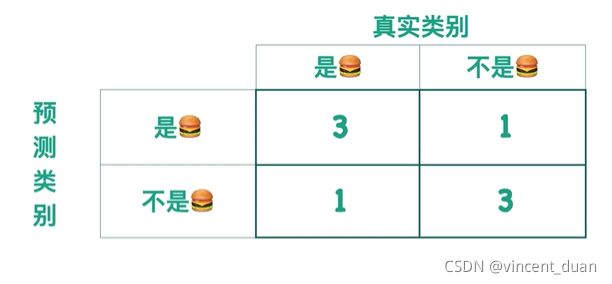
实际上我们的阈值可以取0到1之间的任何数，所以我们可以得到很多个混淆矩阵。

那么有没有一种方法能把所有的混淆矩阵表示在同一个二维空间中呢？这就是ROC曲线（Receiver Operator Characteristic）

对于一个混淆矩阵，我们可以求出TPR和FPR两个指标，将他们表示到二维空间中，TPR表示纵坐标，FPR表示横坐标。当我们有很多混淆矩阵时，对应二维空间中有很多个点，把这些点连起来就形成ROC曲线。

$TPR（TruePositiveRate）=\frac{TP}{P}=\frac{TP}{TP+FN}$ ，即用TP除以样本中正例的数量
$FPR（FalsePositiveRate）=\frac{FP}{N}=\frac{FP}{FP+TN}$，即用FP除以样本中负例的数量

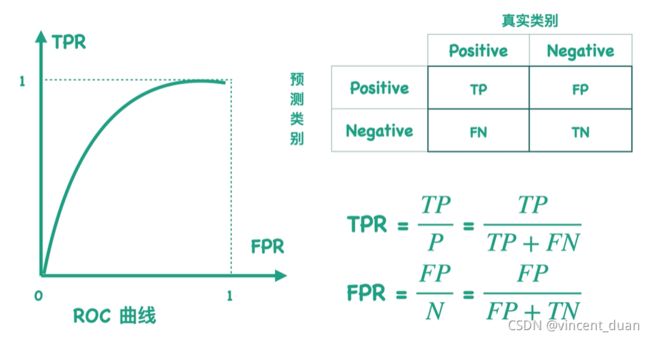
例如下图，当阈值是0到0.1时，分类器会认为所有的图片都是汉堡，就可以得到右上角的混淆矩阵，进而求得对应的TPR和FPR，对应坐标(1,1)：

同理，当阈值是(0.1,0,2]时，我们可以得到新的混淆矩阵。二维空间中有新的点与之对应：

随着阈值不断右移，直到阈值取得最大值，二维空间找到所有对应混淆矩阵的点，我们把这些点连起来，就得到了ROC曲线：

假设我们又有一个分类器B，对应的ROC曲线是蓝色的，如何判断那个曲线效果更好：

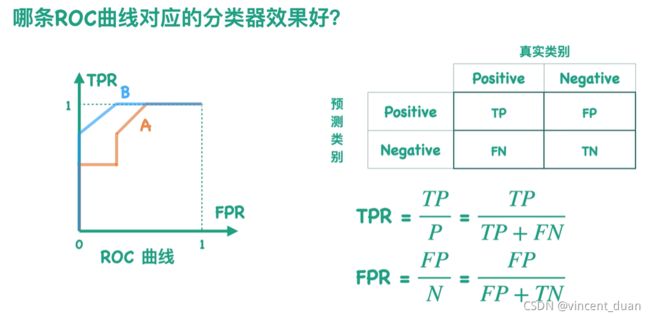
显然TPR和FPR的分母对于同一个测试集是不变的，因为P和N分别表示测试集正负样本的数目，所以TPR与FPR仅仅与TP和FP相关，由于TP正确分类的情况，而FP表示本应属于Negative的样本被错误分类的为Positive的类，所以我们希望TP尽可能大，而FP尽可能小。也就是说我们想让TPR尽可能大，FPR尽可能小。故而在B曲线越靠近左上角效果越好。

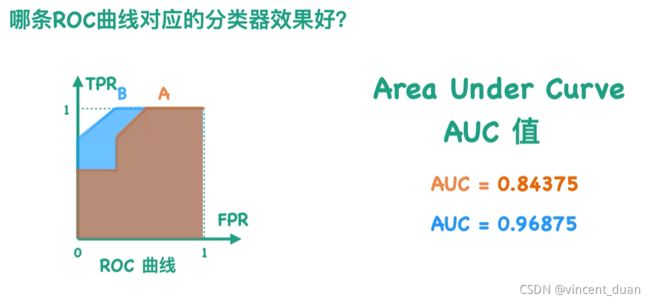
如何通过数值表示这个大小，而不是通过图片来看ROC的大小呢？因为我们通过图片显然看到B曲线比A曲线靠左上方，效果更好。我们可以通过曲线与X轴的面积来表示。这就是我们通常说的AUC值，AUC的取值范围通常是0到1之间，并且越大越好。

对于一个多分类问题，怎么计算AUC呢？

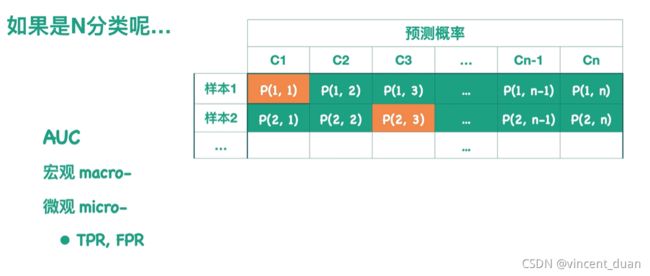
其实它与F1值一样，我们可以求得宏观（macro-）AUC 和微观（micro-）AUC。对于宏观的AUC来说，我们针对每一个类别都可以画一个ROC曲线，求出对应的AUC值，最后对所有的AUC求某种平均做为整个模型所有类别的宏观AUC值，而对于微观的AUC，假设我们概率预测结果如上表所示，每一行表示一个样本在预测成各个类别的概率，例如第一行样本1表示预测成C1类的概率是P(1,1)，预测成C2类的概率为P(1,2)，而橙色方块表示该样本所属的真实类别，例如样本1的真实类别是C1，样本2的真实类别是C3，且每个样本的概率和是1，我们可以得到下图所示的表，根据这个表就可以得到整个模型的ROC曲线：

ROC曲线与PR曲线

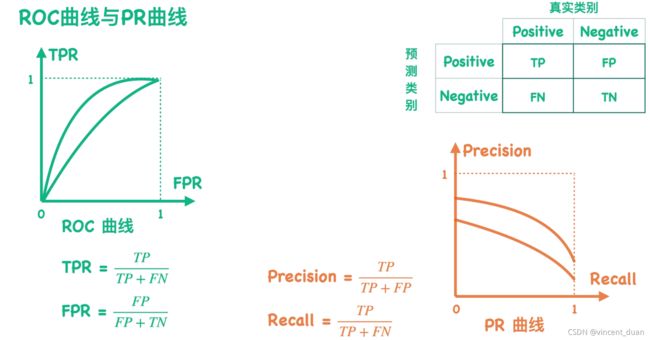
根据上图，当我们设置不同的阈值时，我们会得到不同的混淆矩阵，每个混淆矩阵会对应一个TPR值和一个FPR值，当我们把TPR值和FPR值映射到二维空间中，将点连起来就可以得到一个ROC曲线；

如果我们用precision值代替TPR值，用recall值代替FPR值，将点连起来得到一个新的曲线，这就是PR曲线；

对于一个混淆矩阵来说，有唯一的一对TPR和FPR，以及Precision和Recall，所以可以说每一个ROC曲线都有唯一的一个PR曲线与之对应。

而上面我们介绍到ROC曲线越靠近左上角越好，对于PR曲线来说，我们希望precision值和recall值同时越大越好，所以我们称PR曲线越靠近右上角越好。

ROC曲线与PR曲线的应用场景
根据上面的知识，我们知道，ROC曲线反应的是不同阈值下TPR值和FPR值的关系，而PR曲线反应的是Precision值与Recall值的关系

根据定义我们知道TPR值等于Recall值的，所以这两个曲线的最大区别就是FPR值与Precision值，我们根据公式可以知道FPR值反应的是FP值与测试样本中所有的负例样本的比例，而Precision值是TP值与预测的得到的Positive类别的总数的比例。

举例说明：假设有一个测试集，分类器A和分类器B，分类器的TP值与FN值相同，区别是FP值不同，分类器A的$FP=10TP<<N$，分类器B的$FP=100TP<<N$：

所以我们可以得出一个结论，对于ROC曲线来说，我们对正负两类同样关心，对于PR曲线对正类更加关心。

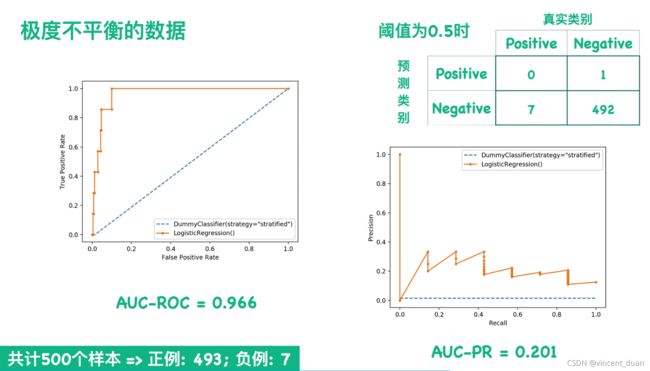
上图中，假设有500个样本，数据极度不平衡，我们画出他的ROC曲线的话得到左边的图，而画出PR曲线得到右下的图，很明显的可以看出右边的图的效果很差，感觉模型不好， 当阈值是0.5时，混淆矩阵是右上角，可以看到正类一个都没有找到，尽管这么差的情况下左边的ROC曲线看上去分类效果很好，因为我们的负类太多了。而右边的PR曲线可以看出我们的模型不太好，所以这种情况下我们应该选取PR曲线。

也就是说我们更关心正类的预测结果，而且我们的数据非常不平衡时，我们应该选用PR曲线而不是ROC曲线。