理论到实际再到工业中AUC的理解

ROC曲线和PR曲线都是样本不平衡中常用的评价指标，可以说他们适用的场景各不相同。这里就引入了几个问题：为什么ROC和PR适用于样本不平衡场景？在样本不平衡的前提下应该如何选择这两个指标，他们的应用场景具体有哪些，他们各自的优缺点是什么，有什么相同点和不同点，AUC和F1-score和他们之间有什么联系，工业界为什么选择ROC曲线（AUC）等等问题

1. 基础知识

1.1 混淆矩阵

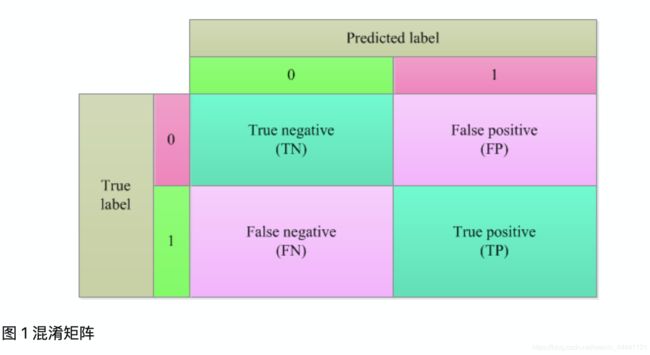
混淆矩阵如图1分别用”0“和”1“代表负样本和正样本。FP代表实际类标签为”0“，但预测类标签为”1“的样本数量。其余，类似推理。

1.2 假正率和真正率

一、首先明确几个基本中的基本概念:

（1）Accuracy = (TN + TP) / (TN + FP + FN + TP)，准确度，表示的是被预测正确的样本占总样本的比例。

（2）Precision = TP / (FP + TP)，精确度，表示在所有被预测为正样本中，真正是正样本的比例。

一、假正率(False Positive Rate，FPR)

计算公式为：

FPR = FP / (FP + TN) ,表示实际标签为”0“的样本中，被预测错误的比例

二、真正率（True Positive Rate，TPR）

又称Recall，即召回率，计算公式为：

TPR/Recall = TP / (TP + FN) ,表示实际标签为”1“的样本中，被预测正确的比例。

三、如何画混淆矩阵从而求解FPR与TPR?

必要条件：

1.用训练集训练好的二分类模型，测试集

2.判断正负样本的阈值threshold

混淆矩阵的画法：

1.首先用模型对测试集进行预测，得到每个测试样本对应的概率值。(不同模型对概率有不同的表达。例如：逻辑回归输出即为概率值；SVM输出到分类界面的距离，称为置信度；决策树输出当前叶子节点中该类样本占总样本的比例)

2.得到预测值后，结合阈值将预测值转换为类别，例如大于阈值时，为正样本，小于阈值时为负样本

3.根据混淆矩阵的定义，计算TN、FN、FP、TP

4.根据FPR和TPR的定义计算其值

利用sklearn混淆矩阵：

import seaborn as sns
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt

sns.set()
f,ax=plt.subplots()
y_true = [0,0,1,2,1,2,0,2,2,0,1,1]  # 真实标签
y_pred = [1,0,1,2,1,0,0,2,2,0,1,1]	# 预测值，一般为model.predict(x_test)
C2= confusion_matrix(y_true, y_pred, labels=[0, 1, 2]) # labels为存在的类别
print(C2) #打印出来看看
sns.heatmap(C2,annot=True,ax=ax) #画热力图

ax.set_title('confusion matrix') #标题
ax.set_xlabel('predict') #x轴
ax.set_ylabel('true') #y轴

2. ROC曲线与经典AUC的理解

2.1 ROC曲线

ROC曲线是一系列threshold下的（FPR，TPR）数值点的连线。此时的threshold的取值分别为测试数据集中各样本的预测概率 (各个概率的顺序是从大到小的)。

二、ROC曲线求解步骤如下：

（1） 首先将预测值从大到小排序

（2） 对于根据预测值排好序的测试样本，按顺序遍历样本，每次遍历时，将当前样本的预测值作为阈值，计算出整个测试集上的FPR和TPR。即假设存在N个测试样本，最终会得到N对(TPR，FPR)

（3）将得到的N对(TPR，FPR)描点，连接，即得到ROC曲线

三、sklearn中画ROC曲线：

首先我们需要了解sklearn.metrics中的roc_curve方法

roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=None)

参数含义：

y_true：简单来说就是label，范围在(0，1)或(-1，1)的二进制标签，若非二进制则需提供pos_label。

y_score：模型预测的类别概率值。

pos_label：label中被认定为正样本的标签。若label=[1,2,2,1]且pos_label=2，则2为positive，其他为negative。

sample_weight：采样权重，可选择一部分来计算。

drop_intermediate：可以去掉一些对ROC曲线不好的阈值，使得曲线展现的性能更好。

返回值：（tpr，fpr，thershold）

tpr：根据不同阈值得到一组tpr值。

fpr：根据不同阈值的到一组fpr值，与tpr一一对应。（这两个值就是绘制ROC曲线的关键）

thresholds：选择的不同阈值，按照降序排列。

有了以上参数和返回值的基础，举个例子来验证一下：

from sklearn.metrics import roc_curve
 
y_label = ([1, 1, 1, 2, 2, 2])  # 非二进制需要pos_label
y_pre = ([0.3, 0.5, 0.9, 0.8, 0.4, 0.6])
fpr, tpr, thersholds = roc_curve(y_label, y_pre, pos_label=2)
 
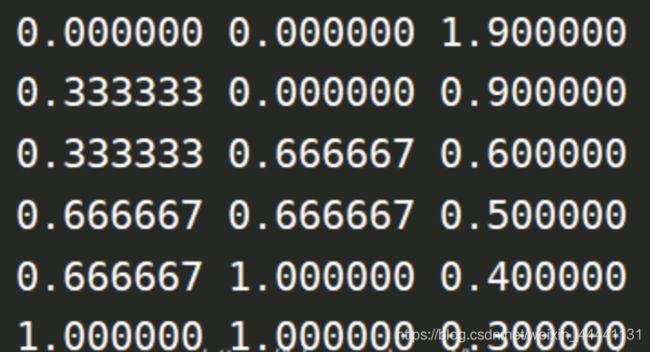
for i, value in enumerate(thersholds):
    print("%f %f %f" % (fpr[i], tpr[i], value))

roc_curve方法中是如何选取阈值？

从输出结果可以看到，第三列代表返回值thersholds记录的就是roc_curve所选取的阈值，其阈值就是将y_pre降序排列并依次选取，如果选取的阈值对fpr和tpr值无影响则忽略，输出结果中没有记录阈值为0.8时情况。

需要注意的是，输出结果第一行therholds=1.9，这个值很奇怪，乍一看不知道为什么会出现这个值。这里我们阅读sklearn官网的原文对therholds这个参数的解释：

Decreasing thresholds on the decision function used to compute fpr and tpr. thresholds[0] represents no instances being predicted and is arbitrarily set to max(y_score) + 1.

thresholds[0] 表示没有任何预测的实例 并且被设置为max(y_score) + 1，这样就知道1.9其实是y_pre中最大的0.9 +1，再简单点来说，第一行其实就是ROC曲线的起点（0，0）。

到这里roc_curve方法的用法应该已经非常清楚了。此时模型的定性分析有了，即ROC曲线，那么定量呢？ AUC登场！

三、AUC求解步骤如下：

计算ROC曲线下的面积即可(一般在实际中，很难根据面积计算，都是采用另一种排序的方法，下面后讲解)

2.2 PR曲线

纵轴Precision，横轴Recall的曲线，对应的定量评估指标最常见的为F1-score = 2*PR/(P+R)

PR曲线和ROC曲线（auc）的关系

2.3 如何选择ROC曲线和PR曲线

The Relationship Between Precision-Recall and ROC Curves中证明了以下两条定理

定理1：对于一个给定的的数据集，ROC空间和PR空间存在一一对应的关系，因为二者包含完全一致的混淆矩阵。我们可以将ROC曲线转化为PR曲线，反之亦然。

定理2：对于一个给定数目的正负样本数据集，曲线 A 在 ROC 空间优于曲线 B ，当且仅当在 PR 空间中曲线 A 也优于曲线 B。

定理 2 中 “曲线A优于曲线B” 是指曲线 B 的所有部分与曲线 A 重合或在曲线 A 之下。而在ROC空间，ROC曲线越凸向左上方向效果越好。与ROC曲线左上凸不同的是，PR曲线是右上凸效果越好。

从定理 2 来看，ROC 空间和 PR 空间两个指标似乎具有冗余性，那么为什么还需要这同时两个指标呢？
答案是在两者在样本不均衡的情况下表现有较大差异，即当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变

文章 ROC和AUC介绍以及如何计算AUC 以及An introduction to ROC analysis 中都认为这是个优点，原因是在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而 ROC 这种对不平衡样本的鲁棒性使得其曲线下的面积 AUC 不会发生突变。

AUC值实际上反映了模型的 rank 能力，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面。这个指标尤其适用在某些场景下(如 CTR 预估)，每次要返回的是最有可能点击的若干个广告(根据CTR排序, 选择排在前面的若干个)，实际上便是在考验模型的排序能力。除此之外，CTR 中存在着样本不均衡的问题，正负样本比例通常会大于 1:100，如果采用 PR 曲线，则会导致 AUC 发生剧变，无法较好反映模型效果

然而，ROC 曲线不会随着类别分布的改变而改变的优点在一定程度上也是其缺点。因为 ROC 曲线这种不变性其实影响着的是 AUC 值，或者说是评估分类器的整体性能。但是在某些场景下，我们会更关注正样本，这时候就要用到 PR 曲线了。

比如说信用卡欺诈检测，我们会更关注 precision 和 recall，比如说如果要求预测出为欺诈的人尽可能准确，那么就是要提高 precision；而如果要尽可能多地预测出潜在的欺诈人群，那么就是要提高 recall。一般来说，提高二分类的 threshold 就能提高 precision，降低 threshold 就能提高 recall，这时便可观察 PR 曲线，得到最优的 threshold。

总结使用场景:

3. AUC的深度理解(工业级别)

例如0.7的AUC，其含义可以大概理解为：任意给定一个正样本和一个负样本，在70%的情况下，模型对正样本的打分高于对负样本的打分。可以看出在这个解释下，我们关心的只有正负样本之间的分数高低，而具体的分值则无关紧要,所以这是AUC的一个很重要的排序解释。

下面解释一下为什么可以将AUC理解为上述情况

TPRate的意义是所有真实类别为1的样本中，预测类别为1的比例。

FPRate的意义是所有真实类别为0的样本中，预测类别为1的比例。

红虚线：上面的点表示无论一个样本本身是正例还是负例，分类器预测其为正例的概率是一样的。例如，上图中B点就是一个随机点，无论是样本数量和类别如何变化，始终将75%的样本分为正例。

ROC曲线围成的面积 (即AUC)可以解读为：从所有正例中随机选取一个样本1，再从所有负例中随机选取一个样本2，分类器将1判为正例的概率比将2判为正例的概率大的可能性。可以看到位于随机线上方的点(如图中的A点)被认为好于随机猜测。在这样的点上TPR总大于FPR，意为正例被判为正例的概率大于负例被判为正例的概率。

从另一个角度看，由于画ROC曲线时都是先将所有样本按分类器的预测概率排序，所以AUC反映的是分类器对样本的排序能力，依照上面的例子就是1排在2前面的概率。
结论：AUC越大，自然排序能力越好，即分类器将越多的正例排在负例之前。

3.1 AUC计算方式(重点)

1、最直观的，根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯 下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么 做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此 时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。

2、一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-Witney Test是等价的。这个等价关系的证明留在下篇帖子中给出。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。有了这个定义，我们就得到了另外一中计 算AUC的办法：得到这个概率。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。这 和上面的方法中，样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数（即n=M+N）

3、第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对score从大到小排序，然后令最大score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。即

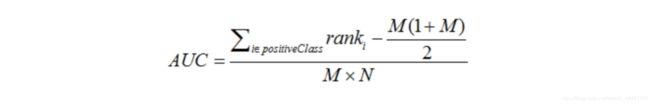
AUC的计算方法及相关总结

公式解释：

1、为了求的组合中正样本的score值大于负样本，如果所有的正样本score值都是大于负样本的，那么第一位与任意的进行组合score值都要大，我们取它的rank值为n，但是n-1中有M-1是正样例和正样例的组合这种是不在统计范围内的（为计算方便我们取n组，相应的不符合的有M个），所以要减掉，那么同理排在第二位的n-1，会有M-1个是不满足的，依次类推，故得到后面的公式M*(M+1)/2，我们可以验证在正样本score都大于负样本的假设下，AUC的值为1

2、根据上面的解释，不难得出，rank的值代表的是能够产生score前大后小的这样的组合数，但是这里包含了（正，正）的情况，所以要减去这样的组（即排在它后面正例的个数），即可得到上面的公式

3.2 AUC对均匀正负样本采样不敏感

正由于AUC对分值本身不敏感，故常见的正负样本采样，并不会导致auc的变化。比如在点击率预估中，处于计算资源的考虑，有时候会对负样本做负采样，但由于采样完后并不影响正负样本的顺序分布。

即假设采样是随机的，采样完成后，给定一条正样本，模型预测为score1，由于采样随机，则大于score1的负样本和小于score1的负样本的比例不会发生变化。

但如果采样不是均匀的，比如采用word2vec的negative sample，其负样本更偏向于从热门样本中采样，则会发现auc值发生剧烈变化。

3.3 AUC值本身有何意义

我们在实际业务中，常常会发现点击率模型的auc要低于购买转化率模型的auc。正如前文所提，AUC代表模型预估样本之间的排序关系，即正负样本之间预测的gap越大，auc越大。

通常，点击行为的成本要低于购买行为，从业务上理解，点击率模型中正负样本的差别要小于购买力模型，即购买转化模型的正样本通常更容易被预测准。

细心的童鞋会想，既然AUC的值和业务数据本身有关，那么它的值为多少的时候算好呢？

3.4 AUC值本身的理论上限

假设我们拥有一个无比强大的模型，可以准确预测每一条样本的概率，那么该模型的AUC是否为1呢？现实常常很残酷，样本数据中本身就会存在大量的歧义样本，即特征集合完全一致，但label却不同。因此就算拥有如此强大的模型，也不能让AUC为1.

因此，当我们拿到样本数据时，第一步应该看看有多少样本是特征重复，但label不同，这部分的比率越大，代表其“必须犯的错误”越多。学术上称它们为Bayes Error Rate，也可以从不可优化的角度去理解。

我们花了大量精力做的特征工程，很大程度上在缓解这个问题。当增加一个特征时，观察下时候减少样本中的BER，可作为特征构建的一个参考指标。

3.5 AUC与线上业务指标的宏观关系

AUC毕竟是线下离线评估指标，与线上真实业务指标有差别。差别越小则AUC的参考性越高。比如上文提到的点击率模型和购买转化率模型，虽然购买转化率模型的AUC会高于点击率模型，但往往都是点击率模型更容易做，线上效果更好。

购买决策比点击决策过程长、成本重，且用户购买决策受很多场外因素影响，比如预算不够、在别的平台找到更便宜的了、知乎上看了评测觉得不好等等原因，这部分信息无法收集到，导致最终样本包含的信息缺少较大，模型的离线AUC与线上业务指标差异变大。

总结起来，样本数据包含的信息越接近线上，则离线指标与线上指标gap越小。而决策链路越长，信息丢失就越多，则更难做到线下线上一致。

3.6 AUC提升和业务指标不一致

好在实际的工作中，常常是模型迭代的auc比较，即新模型比老模型auc高，代表新模型对正负样本的排序能力比老模型好。理论上，这个时候上线abtest，应该能看到ctr之类的线上指标增长。

实际上经常会发生不一致，首先，我们得排除一些低级错误：

1. 排除bug，线上线下模型predict的结果要符合预期。

2. 谨防样本穿越。比如样本中有时间序类的特征，但train、test的数据切分没有考虑时间因子，则容易造成穿越。

3.7 AUC计算逻辑不足与改进

AUC计算是基于模型对全集样本的的排序能力，而真实线上场景，往往只考虑一个用户一个session下的排序关系。这里的gap往往导致一些问题。正如参考[3]中的举例的几个case，比较典型。主要包括两点：

线上会出现新样本，在线下没有见过，造成AUC不足。这部分更多是采用online learning的方式去缓解，AUC本身可改进的不多。

线上的排序发生在一个用户的session下，而线下计算全集AUC，即把user1点击的正样本排序高于user2未点击的负样本是没有实际意义的，但线下auc计算的时候考虑了它。

阿里在论文：Deep Interest Network for Click-Through Rate Prediction中提出了group auc来处理上述问题。公式如下：

即以user为group，在对user的impression做加权平均。私以为，只是对用户做group还不够，应该是基于session去做group。

最后，AUC这个问题是在模型优化到一定程度才需要考虑的。大部分情况下，如果模型的auc有大幅提升，线上效果一般是一致的。如果不一致，请先从产品形态去思考有没有坑。

参考文献

ROC曲线和AUC值的计算
ROC 曲线与 PR 曲线
AUC的计算方法及相关总结
为什么搜索与推荐场景用AUC评价模型好坏？
推荐系统的负采样
机器学习之类别不平衡问题 (2) —— ROC和PR曲线
深入理解实际场景下 AUC vs F1 的区别——不说废话
AUC的理解与计算
图解AUC和GAUC
ROC及AUC计算方法及原理
为什么ROC曲线不受样本不均衡问题的影响