深度强化学习DDPG算法高性能Pytorch代码(改写自spinningup，低环境依赖，低阅读障碍)

写在前面

1. DRL各种算法在github上各处都是，例如莫凡的DRL代码、ElegantDRL（推荐，易读性NO.1）
2. 很多代码不是原算法的最佳实现，在具体实现细节上也存在差异，不建议直接用在科研上。
3. 这篇博客的代码改写自OpenAi spinningup源码DRL_OpenAI，代码性能方面不再是你需要考虑的问题了。
4. 为什么改写？因为源码依赖环境过多，新手读起来很吃力，还有很多logger让人头疼。
5. 这篇博客的代码将环境依赖降低到最小，并且摒弃了一些辅助功能，让代码更容易读懂。
6. 如果本博客的代码在迁移至你的环境时依旧收敛不了，你的reward或者思路存在问题。

项目分三个文件：main.py , DDPGModel.py , core.py
Python3.6

DDPGModel.py

import numpy as np
from copy import deepcopy
from torch.optim import Adam
import torch
import core as core

class ReplayBuffer:   # 输入为size；obs的维度(3,)：这里在内部对其解运算成3；action的维度3
    """
    A simple FIFO experience replay buffer for DDPG agents.
    """

    def __init__(self, obs_dim, act_dim, size):
        self.obs_buf = np.zeros(core.combined_shape(size, obs_dim), dtype=np.float32)
        self.obs2_buf = np.zeros(core.combined_shape(size, obs_dim), dtype=np.float32)
        self.act_buf = np.zeros(core.combined_shape(size, act_dim), dtype=np.float32)
        self.rew_buf = np.zeros(size, dtype=np.float32)
        self.done_buf = np.zeros(size, dtype=np.float32)
        self.ptr, self.size, self.max_size = 0, 0, size

    def store(self, obs, act, rew, next_obs, done):
        self.obs_buf[self.ptr] = obs
        self.obs2_buf[self.ptr] = next_obs
        self.act_buf[self.ptr] = act
        self.rew_buf[self.ptr] = rew
        self.done_buf[self.ptr] = done
        self.ptr = (self.ptr+1) % self.max_size
        self.size = min(self.size+1, self.max_size)

    def sample_batch(self, batch_size=32):
        idxs = np.random.randint(0, self.size, size=batch_size)
        batch = dict(obs=self.obs_buf[idxs],
                     obs2=self.obs2_buf[idxs],
                     act=self.act_buf[idxs],
                     rew=self.rew_buf[idxs],
                     done=self.done_buf[idxs])
        return {k: torch.as_tensor(v, dtype=torch.float32) for k,v in batch.items()}

class DDPG:
    def __init__(self, obs_dim, act_dim, act_bound, actor_critic=core.MLPActorCritic, seed=0,
                replay_size=int(1e6), gamma=0.99, polyak=0.995, pi_lr=1e-3, q_lr=1e-3, act_noise=0.1):

        self.obs_dim = obs_dim
        self.act_dim = act_dim
        self.act_bound = act_bound
        self.gamma = gamma
        self.polyak = polyak
        self.act_noise = act_noise

        torch.manual_seed(seed)
        np.random.seed(seed)

        self.ac = actor_critic(obs_dim, act_dim, act_limit = 2.0)
        self.ac_targ = deepcopy(self.ac)

        self.pi_optimizer = Adam(self.ac.pi.parameters(), lr=pi_lr)
        self.q_optimizer = Adam(self.ac.q.parameters(), lr=q_lr)

        for p in self.ac_targ.parameters():
            p.requires_grad = False

        self.replay_buffer = ReplayBuffer(obs_dim=obs_dim, act_dim=act_dim, size=replay_size)

    def compute_loss_q(self, data):   #返回(q网络loss, q网络输出的状态动作值即Q值)
        o, a, r, o2, d = data['obs'], data['act'], data['rew'], data['obs2'], data['done']

        q = self.ac.q(o,a)

        # Bellman backup for Q function
        with torch.no_grad():
            q_pi_targ = self.ac_targ.q(o2, self.ac_targ.pi(o2))
            backup = r + self.gamma * (1 - d) * q_pi_targ

        # MSE loss against Bellman backup
        loss_q = ((q - backup)**2).mean()

        return loss_q # 这里的loss_q没加负号说明是最小化，很好理解，TD正是用函数逼近器去逼近backup，误差自然越小越好

    def compute_loss_pi(self, data):
        o = data['obs']
        q_pi = self.ac.q(o, self.ac.pi(o))
        return -q_pi.mean()  # 这里的负号表明是最大化q_pi,即最大化在当前state策略做出的action的Q值

    def update(self, data):
        # First run one gradient descent step for Q.
        self.q_optimizer.zero_grad()
        loss_q = self.compute_loss_q(data)
        loss_q.backward()
        self.q_optimizer.step()

        # Freeze Q-network so you don't waste computational effort
        # computing gradients for it during the policy learning step.
        for p in self.ac.q.parameters():
            p.requires_grad = False

        # Next run one gradient descent step for pi.
        self.pi_optimizer.zero_grad()
        loss_pi = self.compute_loss_pi(data)
        loss_pi.backward()
        self.pi_optimizer.step()

        # Unfreeze Q-network so you can optimize it at next DDPG step.
        for p in self.ac.q.parameters():
            p.requires_grad = True


        # Finally, update target networks by polyak averaging.
        with torch.no_grad():
            for p, p_targ in zip(self.ac.parameters(), self.ac_targ.parameters()):
                # NB: We use an in-place operations "mul_", "add_" to update target
                # params, as opposed to "mul" and "add", which would make new tensors.
                p_targ.data.mul_(self.polyak)
                p_targ.data.add_((1 - self.polyak) * p.data)

    def get_action(self, o, noise_scale):
        a = self.ac.act(torch.as_tensor(o, dtype=torch.float32))
        a += noise_scale * np.random.randn(self.act_dim)
        return np.clip(a, self.act_bound[0], self.act_bound[1])

core.py

import numpy as np
import scipy.signal

import torch
import torch.nn as nn


def combined_shape(length, shape=None):  #返回一个元祖(x,y)
    if shape is None:
        return (length,)
    return (length, shape) if np.isscalar(shape) else (length, *shape) # ()可以理解为元组构造函数，*号将shape多余维度去除

def mlp(sizes, activation, output_activation=nn.Identity):
    layers = []
    for j in range(len(sizes)-1):
        act = activation if j < len(sizes)-2 else output_activation
        layers += [nn.Linear(sizes[j], sizes[j+1]), act()]
    return nn.Sequential(*layers)

def count_vars(module):
    return sum([np.prod(p.shape) for p in module.parameters()])

class MLPActor(nn.Module):

    def __init__(self, obs_dim, act_dim, hidden_sizes, activation, act_limit):
        super().__init__()
        pi_sizes = [obs_dim] + list(hidden_sizes) + [act_dim]
        self.pi = mlp(pi_sizes, activation, nn.Tanh)
        self.act_limit = act_limit

    def forward(self, obs):
        # Return output from network scaled to action space limits.
        return self.act_limit * self.pi(obs)

class MLPQFunction(nn.Module):

    def __init__(self, obs_dim, act_dim, hidden_sizes, activation):
        super().__init__()
        self.q = mlp([obs_dim + act_dim] + list(hidden_sizes) + [1], activation)

    def forward(self, obs, act):
        q = self.q(torch.cat([obs, act], dim=-1))
        return torch.squeeze(q, -1) # Critical to ensure q has right shape.


class MLPActorCritic(nn.Module):

    def __init__(self, obs_dim, act_dim, hidden_sizes=(256,256),
                 activation=nn.ReLU, act_limit = 2.0):
        super().__init__()

        # build policy and value functions
        self.pi = MLPActor(obs_dim, act_dim, hidden_sizes, activation, act_limit)
        self.q = MLPQFunction(obs_dim, act_dim, hidden_sizes, activation)

    def act(self, obs):
        with torch.no_grad():
            return self.pi(obs).numpy()

main.py

from DDPGModel import *
import gym
import matplotlib.pyplot as plt


if __name__ == '__main__':
    env = gym.make('Pendulum-v0')
    obs_dim = env.observation_space.shape[0]
    act_dim = env.action_space.shape[0]
    act_bound = [-env.action_space.high[0], env.action_space.high[0]]

    ddpg = DDPG(obs_dim, act_dim, act_bound)

    MAX_EPISODE = 100
    MAX_STEP = 500
    update_every = 50
    batch_size = 100
    rewardList = []
    for episode in range(MAX_EPISODE):
        o = env.reset()
        ep_reward = 0
        for j in range(MAX_STEP):
            if episode > 20:
                a = ddpg.get_action(o, ddpg.act_noise)
            else:
                a = env.action_space.sample()
            o2, r, d, _ = env.step(a)
            ddpg.replay_buffer.store(o, a, r, o2, d)

            if episode >= 10 and j % update_every == 0:
                for _ in range(update_every):
                    batch = ddpg.replay_buffer.sample_batch(batch_size)
                    ddpg.update(data=batch)

            o = o2
            ep_reward += r

            if d:
                break
        print('Episode:', episode, 'Reward:%i' % int(ep_reward))
        rewardList.append(ep_reward)

    plt.figure()
    plt.plot(np.arange(len(rewardList)),rewardList)
    plt.show()

对比

我拿了一个github上写得比较好的Soft-AC算法来和本博客的DDPG算法进行相同环境(倒立摆)比较，reward curve如下：


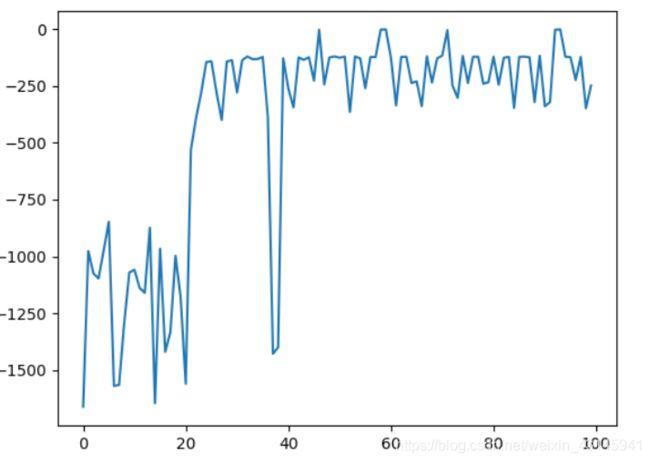
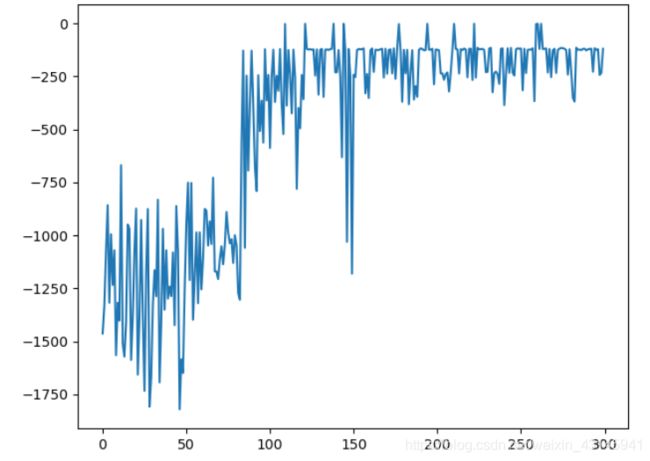
第一张图是本博客DDPG算法，第二张是github上softAC算法，注意看横轴，本博客在20个回合后就收敛了，softAC在第90个回合才逐步收敛。并且：softAC是比DDPG更加先进的算法，先进的算法都差这么多，由此可以看出本博客代码的性能优势。

why

spinningup代码看下来之所以性能高可能在两个方面：

1. 网络架构好
2. 训练方式：前期直接sample动作范围内一个值，这样极大丰富了replay_buffer的信息量，之后才开始更新网络。
3. 参数的选择以及一些细节trick（冻结参数这种操作等）