【算法分析与设计】【期中（末）复习题】【2022秋】

一. 单选题

1.按照渐近阶从低到高的顺序排列下列表达式：

30n，2logn，4，n!

A. 4<30n<2logn B. 30n<4<2logn C. n!<4<2logn<30n
D. `4<2logn<30n

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(n^k) < O(2ⁿ) < O(n!) < O(nⁿ)
（常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 立方阶 < K次方阶 < 指数阶 < 阶乘阶 < n的n次方）

2.二维空间中有n个点，采用蛮力法法求其中距离最近的两个点，对应的算法时间复杂度是（ ）。
A. O(n²)
B. O(n)
C. O(n³)
D. O(nlogn)

3.计算时间复杂度T(n)
$$T(n)=\{\begin{array}{ll}4& \text{n=1}\\ T(n-1)+4& \text{其它}\end{array}$$

A. T(n)=4n
B. T(n)=2n
C. T(n)=8n
D. T(n)=n
解析：三种方法求递归算法的时间复杂度（递推，master定理，递归树）/CSDN@毕业势必进大厂

4.快速排序算法的效率取决于（）
A. 序列是否有序排列
B. 划分的对称性
C. 原始序列是否逆序排列
D. 原始序列是否是正序排列

5.按照渐近阶从低到高的顺序排列下列表达式：

5n²，2logn，n^1/3，4n

A. 4n<5n²<2logn1/3
B. n^1/3<2logn<5n²<4n
C. 2logn1/3< 5n²<4n
D. 5n²<2logn1/3<4n

6.二分搜索算法是利用（ ）实现的算法。
A. 回溯法
B. 蛮力法
C. 分治策略
D. 动态规划

7.贪心算法能求得下面（ ）问题的整体最优解。
A. 活动安排问题
B. 多机调度问题
C. 0/1背包问题
D. n皇后问题

8.记号O的定义正确的是（ ）。
A. O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n≥n₀有：0≤ cg(n) ≤f(n) }；
B. O(g(n)) = { f(n) | 对于任何正常数c>0，存在正数和n₀>0使得对所有n≥n0有：0≤cg(n) < f(n) }；
C. O(g(n)) = { f(n) | 对于任何正常数c>0，存在正数和n₀>0使得对所有n≥n₀有：0 ≤f(n)≤cg(n) }；
D. O(g(n)) = { f(n) | 存在正常数c和n₀使得对所有n≥n₀有：0≤ f(n) ≤ cg(n) }；
解析：算法导论学习 之 渐进符号/博客园@BlackStorm

9.下列算法中通常以自底向上的方式求解最优解的是（ ）。
A. 备忘录法
B. 回溯法
C. 贪心法
D. 动态规划法

10.一个问题可以用动态规划法或贪心法求解的关键特征是问题的（ ）
A. 重叠子问题性质
B. 定义最优解
C. 贪心选择性质
D. 最优子结构性质

11.函数f(n)=2ⁿ，g(n)=3ⁿ，则：（）
A. 2ⁿ=O(3ⁿ)
B. 2ⁿ=Ω(3ⁿ)
C. 2ⁿ=o(3ⁿ)
D. 2ⁿ=θ(3ⁿ)

12.算法分析中，记号Ω表示（）
A. 非紧上界
B. 渐近上届
C. 渐近紧界
D. 渐近下届

13.算法要对异常情况进行适当的处理，就是算法的（）。
A. 可行性
B. 健壮性
C. 正确性
D. 有穷性

14.用枚举法求解0/1背包问题，算法的效率是（ ）
A. 多项式阶
B. 常数阶
C. 指数阶
D. 对数阶

15.动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，他们的主要差别是 （）。
A. 子问题是否容易计算
B. 是自顶向下解决还是自底向上解决
C. 问题能否递归解决
D. 子问题是否相互独立

16.设S是一组n条直线，其中没有两条是平行的，也没有三条在同一点相交。可以证明S中的直线确定了( )个交点。
A. Θ(n)
B. Θ(n²)
C. Θ(n(n-1))
D. Θ(n³)

17.Hanoi塔问题如下图所示。现要求将塔座A上的的所有圆盘移到塔座B上，并仍按同样顺序叠置。移动圆盘时遵守Hanoi塔问题的移动规则。由此设计出解Hanoi塔问题的递归算法正确的为：（ ）

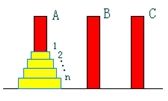
A.

void hanoi（int n,int A,int C,int B）
{  
    if (n>0)
        { 
          hanoi（n-1,A,B,C）; //将A座上的n-1个盘子借助B座移向C座
          move(n,A,B);       //将A座上最后一个盘子移向B座
          hanoi（n-1,C,A,B）;//将C座上的n-1个盘子借助A座移向B座
        }
}

B.

void hanoi（int n,int C,int B,int A）
{  
    if (n>0)
        { 
          hanoi（n-1,A,C,B）;
          move(n,A,B);
          hanoi（n-1,C,B,A）;
        }
}

C.

void hanoi（int n,int A,int C,int B）
{  
    if (n>0)
        { 
          hanoi（n-1,A,C,B）;
          move(n,A,B);
          hanoi（n-1,C,B,A）;
        }
}

D.

void hanoi（int n,int C,int A,int B）
{  
    if (n>0)
        { 
          hanoi（n-1,A,C,B）;
          move(n,A,B);
          hanoi（n-1,C,B,A）;
        }
}

解析：汉诺塔——经典递归问题（c语言实现）/CSDN@小钟hhh

18.函数 f(n)=10，g(n)=log10，则:( )
A. 10=Ω(log10)
B. 10=o(log10)
C. 10=O(log10)
D. 10=θ(log10)

19.给出下面算法的时间复杂性

p = 0；
for( i =0；i<= 2n；i++) 
     p = p*i；

A. O(n)
B. O(n⁴)
C. Ο(2ⁿ)
D. O(n²)

20.函数 f(n)=log2n，g(n)=logn，则 ：（）
A. log²n=O(logn)
B. log²n=o(logn)
C. log²n=θ(logn)
D. log²n=Ω(logn)

二. 填空题

1.下面算法的时间复杂度为（）

void main()
{  
    int m,i,s;
    for(m=2;m<=1000;m++)
    {
        s=0;
        for (i=1;i<=m/2;i++)
            if (m%i==0) 
                s+=i; //i是m的一个因子
            if (m==s)
                printf("%d ",m);
    }
}

1或O(1)

2.蛮力法是一种简单直接地解决问题的方法，也是最低效的方法。典型的（）时间算法一般都是采用蛮力法。

指数

3.利用快速排序算法对下面10个整数进行一次划分，基准为第一个数字2，划分结果为(数字之间以逗号分隔)：

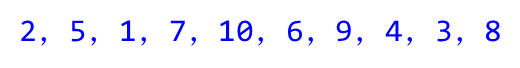
1，2，5，7，10，6，9，4，3，8
或
1,2,5,7,10,6,9,4,3,8

4.Cook论题以多项式时间复杂性为分界线，将可以在多项式时间内解决的问题称为（ ），将在指数时间 解决的问题称为（ ）

(1) 易解问题
(2) 难解问题

5.分治和（）就像孪生兄弟，总是同时应用于算法设计之中。

递归

6.在函数的定义过程中出现了调用此函数的语句，这种函数称为（）函数。

递归

7.算法中描述的操作都可以通过已经实现的基本操作运算有限次实现。这指的是算法的（ ）

可行性

8.蛮力法也称（ ），它的基本思想是采用一定的策略依次处理待求解问题的所有元素，从而找出问题的解。

穷举法
或
枚举法

9.算法的（ ）性质指的是一个算法的执行必须结束。也就是说一个算法它所包含的计算步骤和每个步骤都能在有限时间内完成。

有穷性

10.主程序中调用下面算法f(3),写出程序的输出。

void f(int n)
{　 
    if (n<1) 
        return;
    else
    { 
        printf("n=%d\n"，n);
        f(n-1);
        printf("n=%d\n"，n);
　　}
}

n=3
n=2
n=1
n=1
n=2
n=3

11.函数嵌套调用和返回时 ，函数之间的信息传递和控制转移必须通过（）来实现。

栈

12.一个算法的存储量包括形参所占空间和临时变量所占空间。在对算法进行存储空间分析时，只考察（ ）所占空间。

临时变量

三. 判断题

1.实现分治策略的算法时，只能采用递归函数。
A. 对
B. 错

2.O(1)=O(8)，O(1)和O(8)表示同一个函数时，差别仅在于其中的常数因子。
A. 对
B. 错

3.一个算法的效率用O符号表示时，总是采用最有价值的g(n)表示，称之为“紧凑下界”或“紧确下界”。
A. 对
B. 错

4.Θ符号比O符号和Ω符号都精确，f(n)=Θ(g(n)），只要g(n)既是f(n)的上界又是f(n)的下界。
A. 对
B. 错

答案解析：当且仅当

5.分治策略将求出的小规模的问题的解合并为一个更大规模的问题的解，自顶向下逐步求解原来问题。
A. 对
B. 错

答案解析：自底向上

6.算法分析是分析算法占用计算机资源的情况，即分析算法的时间复杂度。
A. 对
B. 错

7.如果一个算法对其每一个输入实例，都能输出正确的结果并停止，则称它是可靠的。
A. 对
B. 错

8.算法A的运行时间至少是O(),这种说法没有意义
A. 对
B. 错

四. 多选题

1.设n为算法中的问题规模，通常用（）渐进符号表示算法的执行时间与n之间的一种增长关系。
A. Ω
B. Σ
C. O
D. Θ

2.对算法与数据结构关系的描述，正确包括（）。
A. 数据结构是算法设计的基础
B. 算法设计就是在选定的存储结构上设计一个满足要求的好算法
C. 一种数据结构只支持一种算法
D. 算法是编程思想，数据结构是这些思想的逻辑基础

3.分治策略所能解决的问题一般具有以下几个特征（）。
A. 问题的规模缩小到一定程度就可以容易求解
B. 子问题之间相互重叠
C. 子问题的解可以合并出原问题的解
D. 问题可以分解为若干个规模较小的相同问题