代码随想录算法训练营第20天 | 654.最大二叉树 617.合并二叉树 700.二叉搜索树中的搜索 98.验证二叉搜索树

代码随想录系列文章目录

代码随想录 - 二叉树篇

---

---

654.最大二叉树

题目链接
这个题的思路是用前序遍历递归构建一棵二叉树，根结点是什么，根的左子树是什么，右子树是什么
根的值是数组中最大的，然后左右区间很明晰
这道题的思路紧跟106. 根据中序后序数组构建二叉树，但是比它简单

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums: return None

        root_val = max(nums)
        root = TreeNode(root_val)

        seprate_idx = nums.index(root_val)

        nums_left = nums[:seprate_idx]
        nums_right = nums[seprate_idx+1:]

        root.left = self.constructMaximumBinaryTree(nums_left)
        root.right = self.constructMaximumBinaryTree(nums_right)

        return root

617.合并二叉树

题目链接
这道题就考察对两棵二叉树的操作，我们选择用中序遍历，可以新创建一棵树，也可以把第二棵树加在第一棵树上
主要是递归的出口可能不太清晰，如果node2为空，说明return node1即可，反之亦然。他们都为空的情况也不用特判，包含进去了

dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root1: return root2
        if not root2: return root1
        root = TreeNode()
        root.val = root1.val + root2.val
        root.left = self.mergeTrees(root1.left, root2.left)
        root.right = self.mergeTrees(root1.right, root2.right)
        return root

bfs

class Solution:
    def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
        if not root1: 
            return root2
        if not root2: 
            return root1

        queue = deque()
        queue.append(root1)
        queue.append(root2)

        while queue: 
            node1 = queue.popleft()
            node2 = queue.popleft()
            # 更新queue
            # 只有两个节点都有左节点时, 再往queue里面放.
            if node1.left and node2.left: 
                queue.append(node1.left)
                queue.append(node2.left)
            # 只有两个节点都有右节点时, 再往queue里面放.
            if node1.right and node2.right: 
                queue.append(node1.right)
                queue.append(node2.right)

            # 更新当前节点. 同时改变当前节点的左右孩子. 
            node1.val += node2.val
            if not node1.left and node2.left: 
                node1.left = node2.left
            if not node1.right and node2.right: 
                node1.right = node2.right

        return root1

700.二叉搜索树中的搜索

题目链接
二叉搜索树是一个有序树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉搜索树
这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root == None or root.val == val: return root
        if root.val > val: return self.searchBST(root.left,val)
        if root.val < val: return self.searchBST(root.right,val)
        return None

迭代

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。

对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。

中间节点如果大于3就向左走，如果小于3就向右走，如图：

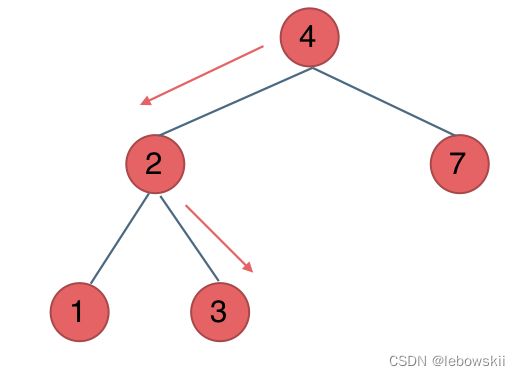
所以迭代法代码如下：

def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        while root != None:
            if root.val > val:
                root = root.left
            elif root.val < val:
                root = root.right
            else:
                return root
        return None

98.验证二叉搜索树

这道题目比较容易陷入两个陷阱：
二叉搜索树的左子树的所有值都小于根节点，右子树所有值都大于根节点

不能简单的判断 left < root < right
1.不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。
我们要比较的是 左子树所有节点小于中间节点，右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。

2.样例中最小节点 可能是int的最小值，如果这样使用最小的int来比较也是不行的。此时可以初始化比较元素为longlong的最小值。

二叉搜索树的递归逻辑一定要写成 左中右

解法1, 把树压缩成数组，判断是不是递增数组

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        # 思路: 利用BST中序遍历的特性.
        # 中序遍历输出的二叉搜索树节点的数值是有序序列
        candidate_list = []
        
        def __traverse(root: TreeNode) -> None: 
            nonlocal candidate_list
            if not root: 
                return 
            __traverse(root.left)
            candidate_list.append(root.val)
            __traverse(root.right)
            
        def __is_sorted(nums: list) -> bool: 
            for i in range(1, len(nums)): 
                if nums[i] <= nums[i - 1]: # ⚠️ 注意: Leetcode定义二叉搜索树中不能有重复元素
                    return False
            return True
        
        __traverse(root)
        res = __is_sorted(candidate_list)
        
        return res

解法2 不用真的压成数组，维护一个当前结点左边的孩子的值，或者说数组中当前正在访问元素的前一个结点

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        # 规律: BST的中序遍历节点数值是从小到大. 
        cur_max = -float("INF")  #其实就是node的左边的一个孩子的值, 因为遍历顺序是左中右，也是展开成数组，正在遍历的数的前一个的值
        def __isValidBST(root: TreeNode) -> bool: 
            nonlocal cur_max
            
            if not root: 
                return True
            
            is_left_valid = __isValidBST(root.left)
            if cur_max < root.val: 
                cur_max = root.val
            else: 
                return False
            is_right_valid = __isValidBST(root.right)
            
            return is_left_valid and is_right_valid
        return __isValidBST(root)