机器学习之k-means算法介绍及python代码实现
目录
- 1.K-means算法介绍
-
- 1.1背景
- 1.2K-means算法理解
- 1.3K-means算法过程
-
- 1.3.1初始化
- 1.3.2归类
- 1.3.3更新质心
- 1.3.3算法停止
- 1.4K-means算法举例
- 2.K-means算法理论推导
- 3.K-means算法代码举例
1.K-means算法介绍
1.1背景
K-mean聚类算法在机器学习中属于无监督学习。所谓“无监督学习”即是指训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。在此类学习任务中研究最多、最广的是“聚类”。
聚类也就是将数据集中的点划分为几个一般情况下不相交的子集、每个子集称为一个“簇”。如下图,在未上色前是一个散点图,通过这些点的位置分布情况,我们可以将他们分为红、绿、蓝三类也就是三个簇。

1.2K-means算法理解
kmeans算法又名k均值算法,K-means算法中的k表示的是聚类为k个簇,means代表取每一个聚类中数据值的均值作为该簇的中心,或者称为质心,即用每一个类的质心对该簇进行描述,那么也就是会有k个质心。在该算法中k值的选择一般是按照实际需求进行决定,或在实现算法时直接给定 k 值。在k-means算法执行结束后,在划分的k个族中同一聚类中的对象相似度较高;而不同聚类中的对象相似度较低。
优点:速度快,简单
缺点:最终结果跟初始点选择相关,容易陷入局部最优,需直到k值
1.3K-means算法过程
总的来看K-means算法就是 以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。
算法介绍

1.3.1初始化
随机从数据集中取k个点作为中心点也就是聚类质心
1.3.2归类
计算各个点到所有簇的质心的距离,将每个点划分到距离质心最近的那个簇
1.3.3更新质心
对于每个簇,利用均值的方法更新该簇的质心
1.3.3算法停止
对于所有的簇的质心,如果利用1.3.2 与1.3.3的迭代法更新后,质心值保持不变,或者变化值小于初始时给定的阈值,则迭代结束,否则继续迭代。
1.4K-means算法举例
数据集:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 4 | 3 |
| 5 | 4 |
**要求:**将以上数据集分为两个簇

初始化(1,1),(2,1)作为簇1,簇2的质心
第0次迭代:

显然根据最短距离划分,我们将A(1,1)划分簇1,将到B(2,1) C(4,3)D(5,4)划分到簇2,然后根据均值计算法得到簇1质心为(1,1),簇2质心为(11/3,8/3)
更新质心后的结果为
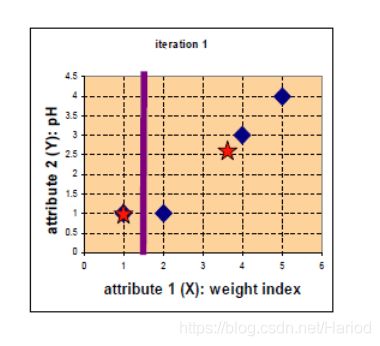
显然根据最短距离划分,我们将A(1,1) B(2,1) 划分簇1,将到 C(4,3)D(5,4)划分到簇2,然后根据均值计算法得到簇1质心为(3/2,1),簇2质心为(9/2,7/2)
更新质心后的结果为

第2次迭代:

显然根据最短距离划分,我们将A(1,1) B(2,1) 划分簇1,将到 C(4,3)D(5,4)划分到簇2,显然与第1次迭代得到的簇的划分相同,那么质点的更新也与第0此得到的值一样。所以符合1.3.3中的算法停止条件,此时算法停止。
最后我们得到的数据集划分结果为
| x | y | 簇号 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 4 | 3 | 2 |
| 5 | 4 | 2 |
2.K-means算法理论推导
暂无
3.K-means算法代码举例
下面我们以上面举的例子中的数据来具体看看K-means算法的简单代码实现
import numpy as np
def kmeans(X, k, maxIt):
'''
:param X:数据集
:param k:分类数
:param maxIt:循环次数
:return:
'''
#矩阵X的横向数与纵向数赋值
numPoints, numDim = X.shape
#创建一个横向数与X相同,纵向数与numDim+1相同的0矩阵
dataSet = np.zeros((numPoints, numDim + 1))
print('dataSet',dataSet)
#把X赋值给dataSet除最后一列的数据
dataSet[:, :-1] = X
print(dataSet)
# 初始化中心点,随机选取两个点作为中心点
centroids = dataSet[np.random.randint(numPoints, size=k), :]
print('centroids',centroids)
centroids = dataSet[0:2, :]
print(centroids)
centroids[:, -1] = range(1, k + 1)
print(centroids)
iterations = 0
oldCentroids = None
while not shouldStop(oldCentroids, centroids, iterations, maxIt):
print("iteration: \n", iterations)
print("dataSet: \n", dataSet)
print("centroids: \n", centroids)
oldCentroids = np.copy(centroids)
iterations += 1
updateLabels(dataSet, centroids)
centroids = getCentroids(dataSet, k)
return dataSet
def shouldStop(oldCentroids, centroids, iterations, maxIt):
if iterations > maxIt:
return True
return np.array_equal(oldCentroids, centroids)
def updateLabels(dataSet, centroids):
numPoints, numDim = dataSet.shape
for i in range(0, numPoints):
dataSet[i, -1] = getLabelFromClosestCentroid(dataSet[i, :-1], centroids)
def getLabelFromClosestCentroid(dataSetRow, centroids):
label = centroids[0, -1];
minDist = np.linalg.norm(dataSetRow - centroids[0, :-1])
for i in range(1, centroids.shape[0]):
dist = np.linalg.norm(dataSetRow - centroids[i, :-1])
if dist < minDist:
minDist = dist
label = centroids[i, -1]
print("minDist:", minDist)
return label
def getCentroids(dataSet, k):
result = np.zeros((k, dataSet.shape[1]))
for i in range(1, k + 1):
oneCluster = dataSet[dataSet[:, -1] == i, :-1]
result[i - 1, :-1] = np.mean(oneCluster, axis=0)
result[i - 1, -1] = i
return result
x1 = np.array([1, 1])
x2 = np.array([2, 1])
x3 = np.array([4, 3])
x4 = np.array([5, 4])
testX = np.vstack((x1, x2, x3, x4))
print("testx",testX)
result = kmeans(testX, 2, 10)
print("final result:")
print(result)
