Python的遗传算法GA优化深度置信网络DBN超参数回归预测
DBN超参数众多,包括隐含层层数、各层节点数、无监督预训练阶段的训练次数及其学习率、微调阶段的训练次数及其学习率、与Batchsize,如果采用SGD相关优化器,还有动量项这个超参数。总之就是特别多,手动选择的话很难选到最佳超参数组合,为此采用遗传算法对上述超参数进行优化。
之前写过MATLAB版本的DBN超参数优化,今天这个是python/torch版本的DBN超参数优化。具体运行环境python36、torch1.2。
话不多说,直接上结果。数据结构是多输入单输出,按照7:3随机划分训练集与测试集。
1、DBN预测,代码如下
# -*- coding: utf-8 -*-
# DBN建模
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
from sklearn.preprocessing import StandardScaler,MinMaxScaler
from sklearn.model_selection import train_test_split
from scipy.io import savemat,loadmat
from sklearn.metrics import r2_score
import warnings
warnings.filterwarnings("ignore")
import torch
from utils.DBN import DBN
device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
seed=0
if device == 'cuda':
torch.cuda.manual_seed(seed) # 为当前GPU设置随机种子
torch.cuda.manual_seed_all(seed) # if you are using multi-GPU,为所有GPU设置随机种子
else:
torch.manual_seed(seed) # 为CPU设置随机种子
# In[] 加载数据
data=pd.read_csv('data1.csv',header=None)
input_data=data.iloc[:,:-1].values
output_data=data.iloc[:,-1].values.reshape(-1,1)
# 归一化
#ss_X = StandardScaler().fit(input_data)
#ss_y = StandardScaler().fit(output_data)
ss_X=MinMaxScaler(feature_range=(0,1)).fit(input_data)
ss_y=MinMaxScaler(feature_range=(0,1)).fit(output_data)
input_data = ss_X.transform(input_data)
output_data = ss_y.transform(output_data)
# 划分样本
x_train,x_valid, y_train, y_valid = train_test_split(input_data,output_data,test_size=0.3,random_state=0)
# In[] 模型构建与训练
start_time=time.time()
#超参数设置
input_length = x_train.shape[1]
output_length = y_train.shape[1]
# network
# rbm的学习率和迭代次数,无监督逐层预训练
learning_rate=0.1
epoch_pretrain = 10
# 隐含层
hidden_units = [20,15]
# batchsize
batch_size = 64
# 微调阶段dbn采用SGD优化器,学习率,迭代次数,动量,激活函数(4选1),损失函数为均方差
learning_rate_finetune=0.1
epoch_finetune = 100
momentum=0.9
tf='Sigmoid'# Sigmoid ReLU Tanh Softplus
loss_function = torch.nn.MSELoss(reduction='mean') # 均方差损失
optimizer = torch.optim.SGD
# Build model
dbn = DBN(hidden_units, input_length, output_length,learning_rate=learning_rate,activate=tf, device=device)
# 无监督预训练dbn中各rbm
dbn.pretrain(x_train, epoch=epoch_pretrain, batch_size=batch_size)
# 有监督微调
dbn.finetune(x_train, y_train, epoch_finetune, batch_size, loss_function,
optimizer(dbn.parameters(), lr=learning_rate_finetune, momentum=momentum),
validation=[x_valid,y_valid],shuffle=True,types=1)
plt.figure()
plt.plot(dbn.finetune_train_loss,label='train_loss')
plt.plot(dbn.finetune_valid_loss,label='valid_loss')
plt.legend()
plt.title('Loss Curve')
plt.show()
# In[] Make prediction and plot
y_predict = dbn.predict(x_valid, batch_size,types=1)
y_predict=y_predict.cpu().numpy()
end_time=time.time()
print('Time cost: %f s'%(end_time-start_time))
# 对测试结果进行反归一化
test_pred = ss_y.inverse_transform(y_predict)
test_label = ss_y.inverse_transform(y_valid)
# In[]
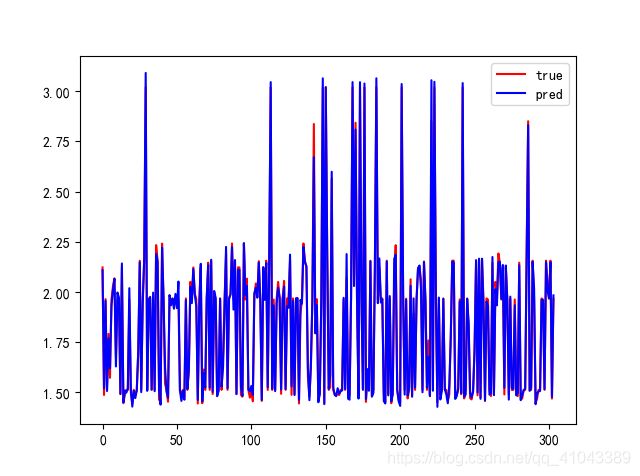
# 画出测试集的值
plt.figure()
plt.plot(test_label,c='r', label='true')
plt.plot(test_pred,c='b',label='pred')
plt.legend()
plt.show()
# In[]计算各种指标
# mape
test_mape=np.mean(np.abs((test_pred-test_label)/test_label))
# rmse
test_rmse=np.sqrt(np.mean(np.square(test_pred-test_label)))
# mae
test_mae=np.mean(np.abs(test_pred-test_label))
# R2
test_r2=r2_score(test_label,test_pred)
print('测试集的mape:',test_mape,' rmse:',test_rmse,' mae:',test_mae,' R2:',test_r2)
结果如下:
指标如下:
mape: 0.02131540499483512
rmse: 0.06900334093296646
mae: 0.04012139316438816
R2: 0.9663487401772392
2、遗传优化DBN超参数
本文利用GA对DBN的超参数进行寻优,以最小化DBN预测值与实际值的MSE为适应度函数,目的就是通过GA找到一组超参数,用这组超参数训练的DBN,具有最小的网络误差。寻优参数及其范围设置如下:
lb=[0.01,0.01,0.1,1 ,1, 1, 1,10]
ub=[0.1, 0.5, 1,21,201,257,4,101]
#预训练学习率的范围是0.01到0.1
#微调训练学习率的范围是0.01到0.5
#动量0.1到1
#rbm迭代次数是1到20,
#dbn微调的迭代次数是1到200
#batchsize是1到256
#隐含层数量是1到3
#隐含层节点数是10-100操作要点:
1)前3个超参数是浮点型、后面的都是整型
2)遗传算法每条DNA的长度是10,就是前7个参数是两个学习率、动量项、两个训练迭代次数、batchsize与层数,因为我们程序设置的最大隐含层是3(ub中是4,是因为random.int这个函数是左闭右开),所以一共10维,即使某DNA中层数是2,也是10维,只不过最后1层为0,例如:
[0.1,0.5,0.9,10,25,64,1,10,0,0],则代表两个学习率分别为0.1 0.5;动量为0.9; 两个迭代次数分别是10,25,batchsize是64,隐含层层数是1,神经元为[10]
[0.1,0.5,0.9,10,25,64,2,10,15,0],则代表两个学习率分别为0.1 0.5;动量为0.9; 两个迭代次数分别是10,25,batchsize是64,隐含层层数是2,各层神经元分别为[10,15]
[0.1,0.5,0.9,10,25,64,5,10,15,20],则代表两个学习率分别为0.1 0.5;动量为0.9; 两个迭代次数分别是10,25,batchsize是64,隐含层层数是3,各层神经元分别为[10,15,30]
当然哈,ub中这个参数是可调的,随便设都行,只要大于1。
3)交叉操作的时候,隐含层层数这个参数不交叉,因为两个DNA如果层数不一致,交叉了的话,后面的节点数就不对了。如果要交叉这个参数的话,就把后面各层的节点数一起进行交叉。
4)变异的时候,隐含层层数发生改变之后,先把该条DNA的各层节点数全部置0 ,然后重新根据层数进行赋值。
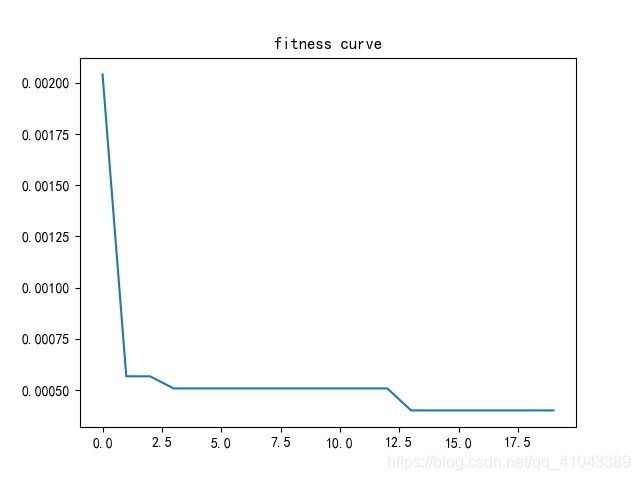
寻优结果适应度曲线如图所示。
对应GA每代优化后的最优超参数组合如下表所示。可见最优DBN的隐含层层数为3层,各层的节点数是92、35、54。
取最后一代优化得到的最优超参数组合(就是第9行那个)用来训练DBN,得到的结果如下:
3、结果对比