VSC/SMC(十五)——基于模糊逼近的积分滑模控制
目录
前言
1. 一阶系统积分滑模
1.1 一阶系统
1.2 控制器设计
1.2.1 选取积分滑模面
1.2.2 选取指数趋近律
1.2.3 Lypunov闭环系统稳定性证明
1.3 仿真分析
1.4 仿真结果
2.基于模糊切换增益调节的滑模控制
2.1为什么需要结合模糊控制?
2.2 模糊工具箱的使用
2.3 m语言设计模糊规则
2.3系统
2.4控制器设计
2.5仿真分析
2.6 仿真结果
2.6.1 普通切换增益
2.6.2 基于模糊控制的(自适应)切换增益
2.6.3 基于饱和函数的切换增益
2.7 总结
3.基于模糊控制的积分滑模控制
前言
积分滑模的优点
由于积分滑模是通过合理设定积分器的初始状态,使系统的初始状态一开始就处于滑模面上,从而消除到达段,以提高控制系统的鲁棒性。
如,设定积分器的初始状态:
选定积分滑模面:
则:
上式表明,通过设计积分项的初始值,就能使系统状态在初始时刻处于滑模面上,不存在到达阶段,保证了系统的鲁棒性。
1. 一阶系统积分滑模
一阶系统为什么要选取积分滑模面?往后看,顺着推导便会明白了。
1.1 一阶系统
![]()
其中,扰动边界为d(t) ≤ D。
1.2 控制器设计
1.2.1 选取积分滑模面
其中,c > 0,所切换面导数为:
![]()
取s' = 0,则等效控制项:
1.2.2 选取指数趋近律
![]()
则鲁棒项:
所以滑模控制律:
![]()
1.2.3 Lypunov闭环系统稳定性证明
![]()
则有:
解为:
![]()
这里可见,V(t)以指数的形式收敛至0,从而s(t)以指数的形式收敛至0,从而滑模面积分项收敛至0,而收敛速度取决于k,当k较大时,收敛速度快,但是抖阵会增大,所以需要设计者折中调节。
1.3 仿真分析
扰动d(t)选取随机数,位置指令xd = sint
1.4 仿真结果
2.基于模糊切换增益调节的滑模控制
2.1为什么需要结合模糊控制?
因为实际中被控对象是标称系统,且存在时变的扰动,但是如果我们的滑模控制律增益是固定的,不能随系统和扰动不确定变化,就会导致抖动过大,或者说鲁棒性差,所以结合自适应模糊控制理论,便能得到自适应切换控制增益,或者说使切换增益。
2.2 模糊工具箱的使用
①在命令行中输入“fuzzy”指令,打开模糊工具箱,并且可以进行与或方法模糊化及去重心法模糊化等选择,一般没有特别要求保持默认即可,如下:
如果需要添加输入或输出端口数量,点击Add Variable即可 ,如下所示:
②双击input1或者output1进入隶属度函数定义界面,如下所示:
③Remove All MFs(移除隶属度函数),Add Custom MF(添加隶属度函数),之后选择输入短隶属度函数个数,本仿真案例这里输入输出都是选择5个。
④定义隶属度函数范围(依据控制要求定义,具体可以参考自己研究的相关文献)、名称/模糊集(一般5个或者7个,如7个:负大,负中,负小,零,正小,正中,正大)、类型(一般两端高斯,中间选择三角)和参数范围,如下:
同样输入端也一样。
⑤定义模糊规则,操作如下:
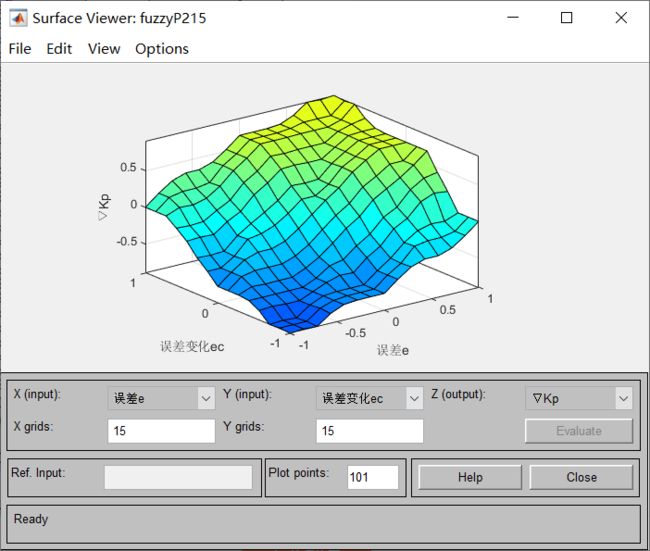
⑥点击“view”,查看定义好的模糊规则和曲曲面
⑦定义好之后进行保存
到这里就用模糊工具箱设计好模糊规则了。
可以选择导出工作区间或者导入到文件保存(推荐,因为可以下次直接调用,调用之后直接再导入到工作区间即可使用),导出.fis文件如下:
[System]
Name='8_1'
Type='mamdani'
Version=2.0
NumInputs=1
NumOutputs=1
NumRules=5
AndMethod='min'
OrMethod='max'
ImpMethod='min'
AggMethod='max'
DefuzzMethod='centroid'
[Input1]
Name='e'
Range=[-15 15]
NumMFs=5
MF1='NB':'zmf',[-15 -5]
MF2='NM':'trimf',[-15 -10 0]
MF3='ZO':'trimf',[-10 0 10]
MF4='PM':'trimf',[0 10 15]
MF5='PB':'smf',[5 15]
[Output1]
Name='u'
Range=[-1.5 1.5]
NumMFs=5
MF1='NB':'zmf',[-1.5 -0.5]
MF2='NM':'trimf',[-1 -0.5 0]
MF3='ZO':'trimf',[-0.5 0 0.5]
MF4='PM':'trimf',[0 0.5 1]
MF5='PB':'smf',[0.5 1.5]
[Rules]
5, 5 (1) : 1
4, 4 (1) : 1
3, 3 (1) : 1
2, 2 (1) : 1
1, 1 (1) : 1
2.3 m语言设计模糊规则
也可以用m语言实现,程序如下:
clear all;
close all;
a=newfis('smc_fuzz');
f1=5;
a=addvar(a,'input','sds',[-3*f1,3*f1]); % Parameter e
a=addmf(a,'input',1,'NB','zmf',[-3*f1,-1*f1]);
a=addmf(a,'input',1,'NM','trimf',[-3*f1,-2*f1,0]);
a=addmf(a,'input',1,'Z','trimf',[-2*f1,0,2*f1]);
a=addmf(a,'input',1,'PM','trimf',[0,2*f1,3*f1]);
a=addmf(a,'input',1,'PB','smf',[1*f1,3*f1]);
f2=0.5;
a=addvar(a,'output','dk',[-3*f2,3*f2]); %Parameter u
a=addmf(a,'output',1,'NB','zmf',[-3*f2,-1*f2]);
a=addmf(a,'output',1,'NM','trimf',[-2*f2,-1*f2,0]);
a=addmf(a,'output',1,'Z','trimf',[-1*f2,0,1*f2]);
a=addmf(a,'output',1,'PM','trimf',[0,1*f2,2*f2]);
a=addmf(a,'output',1,'PB','smf',[1*f2,3*f2]);
rulelist=[1 1 1 1; %Edit rule base
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a1=addrule(a,rulelist);
a1=setfis(a1,'DefuzzMethod','centroid'); %Defuzzy
writefis(a1,'smc_fuzz');
a1=readfis('smc_fuzz');
figure(1);
plotmf(a1,'input',1);
figure(2);
plotmf(a1,'output',1);运行结果:
2.3系统
其中f已知,E为不确定扰动,这里选用一个高斯函数形式的扰动,其函数如下:
取bi = 0.5,ci = 0.5,t为时间。
函数图像实现程序:
clear all;
close all;
b=0.5;
c=5;
ts=0.001;
for k=1:1:10000
t(k)=k*ts;
E(k)=200*exp(-(t(k)-c)^2/(2*b^2));
end
figure(1);
plot(t,E);
xlabel('time(s)');
ylabel('Gaussian function');运行结果:
2.4控制器设计
关于控制律如何得到的,以及Lypunov稳定证明,这里为了节省篇幅不再叙述,可以看我往期文章。
定义输入的模糊集合:
![]()
定义输出的模糊集合:
![]()
采用积分法对切换增益进行估计(即随时变扰动进行调整增益):
所以上述控制律变为:
对于K^其实可以这样理解:因为扰动是时变的,所以传统的切换增益|E| ≤ K()其中K为常数,但是这样的切换增益不能随扰动自适应变化,所以在实际过程中会导致抖阵;而结合模糊控制理论实现K为自适应切换增益。
2.5仿真分析
注:对于Fuzzy Logic Controller模块使用:
法① 可以'模糊系统文件名'(.fis格式后缀可不加);
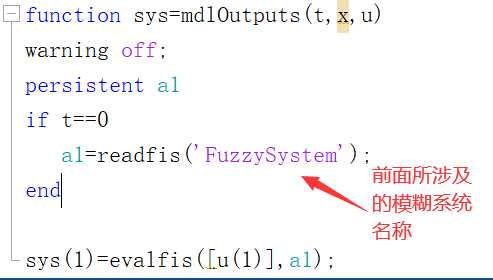
法② 或者使用readfis函数读取到工作区间,用工作区间的工作名称(不加单引号),以模糊系统文件名为FuzzySystem为例,如下:
法①
法②
模型这里也可以用函数编写提取模糊逻辑控制模块,如:
例如用s函数:
2.6 仿真结果
2.6.1 普通切换增益
先让我们来看一下普通切换增益的情况,即切换增益K = D+η,由于|d(t)| ≤ 200,所以取D = 200,η = 1。
2.6.2 基于模糊控制的(自适应)切换增益
扰动估计与实际扰动对比
2.6.3 基于饱和函数的切换增益
2.7 总结
①可以看到基于模糊增益调节的滑模控制,相比普通符号函数切换增益,有较好的消抖效果,但是对于跟踪效果以及消抖的能力完全靠经验取调节,如模糊规则、采用积分法对切换增益的估计比例系数等等,比较繁琐,可能后面会进行改进。
②可以看到基于饱和切换函数的跟踪效果和消抖情况是这三者面最好的,而且简单。
③根据我的理解,所谓的自适应切换增益即用模糊逼近的远离逼近不确定,使得切换增益是逼近不确定量大小,从而能达到消抖得目的。
3.基于模糊控制的积分滑模控制
未完待续......
如果有帮助,麻烦帮忙点个赞是我最大的分享动力,非常感谢!
注:仅为便利自己学习,错误在所难免,如有侵权,请联系删除,有兴趣的学者可以参考学习交流,谢谢!
参考资料:
- 管成,朱善安. 一类非线性系统的微分与积分滑模自适应控制及其在电液伺服系统中的应用.