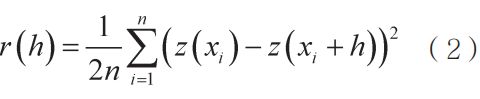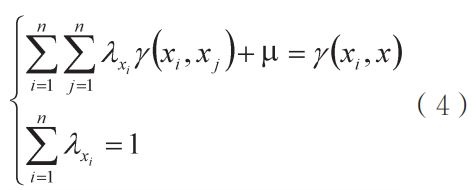基于主动学习和克里金插值的空气质量推测

基于主动学习和克里金插值的空气质量推测

常慧娟, 於志文, 於志勇, 安琦, 郭斌

西北工业大学计算机学院，陕西 西安 710072 福州大学数学与计算机科学学院，福建 福州 350108 

 

摘要：空气质量监测站仅能在少数位置部署，故而无法获取城市中每个位置的空气质量信息。提出了一种基于主动学习和克里金插值的空气质量推测算法。该算法首先选用克里金插值作为基础的空气质量推测算法，然后结合主动学习的思想，对置信度最大的位置进行优先采样，最终建立基于主动学习的插值模型，通过最少的监测点对空气质量进行采样，最大限度地提升推测其他位置空气质量的准确度。研究结果表明，所提算法能够有效地提高空气质量推测精度，同时减少监测站采样数量，降低部署成本。

关键词：克里金插值 ; 空气质量指数 ; 主动学习 ; 空间插值 ; 空气质量推测

论文引用格式：

常慧娟, 於志文, 於志勇, 安琦, 郭斌. 基于主动学习和克里金插值的空气质量推测. 大数据[J], 2018, 4(6):54-64CHANG H J, YU Z W, YU Z Y, AN Q, GUO B. Air quality estimation based on active learning and Kriging interpolation. Big data research[J],2018,4(6):54-64

1 引言

随着社会经济的发展和人民生活水平的提高，空气质量越来越被大家所关注。空气一直是维护人类及生物生存的保护膜，对人类及生物生存起着重要作用。但随着工业及交通运输业的不断发展，大量的有害物质被排放到空气中，空气质量每况愈下，由其导致的酸雨和全球变暖问题都在破坏着人类的自然环境和生态系统。在循环经济、绿色经济、经济与环境可持续发展的趋势下，为了了解空气污染变化趋势，掌握及时、准确、全面的空气质量信息，需要对空气质量进行精准预测，准确获取城市中每个位置的空气质量成为一项必不可少的研究工作，可为监控空气污染状况、制定治理措施提供依据。但由于空气质量监测站需占用大量空间且成本高昂，仅能在少数位置部署，因此选取哪些位置对空气质量进行采样，从而最大限度地推测其他位置的空气质量，是一项具有挑战的工作。基于空气质量数据不足的情况，本文选用克里金（Kriging）插值并结合主动学习的思想，提出用于空气质量指数 推测的Kriging模型。

目前，对同一地区的未来某时的空 气质量指数以及污染物浓度预测已经有很多研究工作了，然而对同一时刻，指定地区的空气质量推测还没有很好的探索。空气质量具有空间自相关性，因此一个简单的方法是使用Kriging模型进行空间插值预测。在用Kriging方法建模的过程中，标记样本数量的多少直接关系到模型的精度，当标记样本较少时，通常难以构建可靠的模型。在传统的监督学习环境中，应该提供大量的训练样例来构建具有良好泛化能力的模型。需要指出的是，这些训练样例应该加上标签，而在许多实际的机器学习和数据挖掘应用中，通常只有少数标记训练示例是可用的，在实际应用中，空气质量监测站占用了大量的空间且成本高昂，对于大多数位置而言，并没有任何空气质量数据。为了提高预测精度，提出一种基于主动学习的Kriging（active-learning Kriging，ALK）插值方法，用于推测给定的任意位置的空气质量指数。本文的主要工作如下：

● 提高对给定的任意位置的空气质量指数预测的准确度；

● 提出了一个基于主动学习的Kriging插值模型，该模型通过选取少数位置对空气质量进行采样，能最大限度地提升推测其他位置的空气质量的准确度；

● 使用我国43个城市的数据来评估提出的模型，实验结果验证了本文预测框架的通用性和有效性，并提高了预测精度。

2 相关工作

目前，一些关于分析和预测空气质量的研究工作已达到对大气环境质量进行预测预警的作用。这些研究工作采用了不同的方法对空气质量进行预测。在环境科学方面，现有的空气质量预测方法通常基于经典的离散模型，如高斯烟羽（Gaussian plume）模型、与监管街道峡谷相关的模型（operational street canyon模型）和计算流体动力学（computational fluid dynamics）模型。近年来，一些统计模型（如线性回归模型、回归树模型和神经网络模型）已被应用于大气科学，实时预测空气质量。宋宇辰等人和祝翠玲等人运用时间序列法和反向传播（back propagation,BP）神经网络法建立模型，预测空气质量，对SO2、NO2和可吸入颗粒物的浓度值进行预测与分析；郑宇等人使用数据驱动的方法预测未来48 h的空气质量监测站的读数，该数据驱动的方法考虑了当前的气象数据、天气预报、监测站空气质量数据以及该监测站周围几百公里其他监测站的空气质量数据；林开春等人和孟倩提出基于随机森林的空气质量指数预测模型和空气质量等级分类预测方法。苏静等人和杨锦伟等人应用灰色理论模型预测空气质量变化趋势，对未来10年的污染因子浓度进行了预测；闫妍等人提出了一种基于神经网络的环境空气质量的预测方法，他们运用BP人工神经网络的多层神经网络对西安市大气污染物浓度的实测值进行了训练学习，建立了模型，并用此模型对污染物浓度进行了预测和预报。

然而，所有先前研究工作的有效性和可用性都是基于已有的监测站数据，从时间序列的自相关性预测未来某个时间的空气质量污染物浓度。如果某地没有空气质量监测站，想要预测该位置的空气质量仍然是一个难题。本文尝试利用空间插值的方法来解决这个问题，并提出一个基于主动学习的Kriging插值模型，以使用最少的数据达到高精度预测的目标。

3 问题陈述和系统概述

3.1 问题陈述

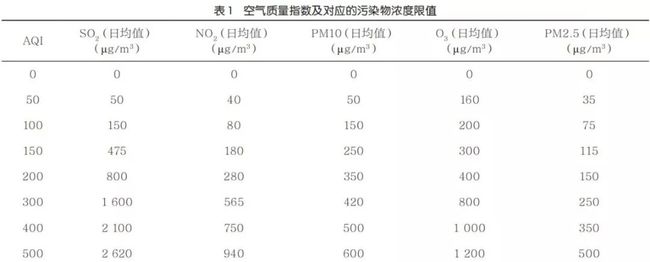
空气质量指数（air quality index， AQI）是政府机构向公众传达空气污染程度的指标。在环境监测部门每天发布的空气质量报告中，包含各种污染物的浓度值，但对于大多数人而言，这些抽象的数据并没有很具体的意义，无法从这些数据中判断出当前的空气质量到底处在什么水平。于是根据环境空气质量标准和各项污染物对人体健康、生态、环境的影响，将常规监测的几种空气污染物浓度简化为单一的概念性指数值，即AQI，通过这一数值，人们可以一目了然地判断出空气质量的高低。

参与空气质量评价的主要污染物为细颗粒物、可吸入颗粒物、SO2、NO2、O3等。具体来说，空气监测站会监测并记录空气质量数据，从中可以获得PM2.5、PM10、SO2、NO2、O3污染物的浓度信息，通过计算可以获得AQI，计算式如下：

其中，为空气质量指数，即AQI；C为污染物浓度；Cl、Ch为该污染物浓度限值，Il、Ih为对应的AQI限值，4个数均为常量，可查阅表1获得。

本文用AQI来描述空气质量的好坏，目标是识别AQI与空间位置之间的关系，并建立有效的模型，当给定指定地区的空间位置时，即可预测该位置的空气质量指数。

3.2 系统概述

图1展示了预测空气质量指数的ALK模型的框架。首先从原始数据集中获取污染物浓度数据以及空气监测站数据，并将其提取为两个特性：AQI、监测站空间位置（经度、纬度）。之后用算法建立这些因素之间的关系，其中，输入值是地理位置信息，输出值是相应的AQI。最后，利用历史数据集，验证提出的预测模型是否能够有效地预测指定位置的AQI。

图1 框架概述

4 空气质量推测模型

本节将对基于主动学习的克里金插值模型以及相关知识进行详细介绍。

4.1 克里金插值

空间插值问题就是在已知空间上若干离散点的某一属性值的条件下，估计空间上任意一点(x,y)的这一属性值的问题。克里金插值法又称空间自协方差最佳插值法。它首先考虑的是空间属性在空间位置的变异分布，确定一个对待插点的属性值有影响的距离范围，然后用此范围内的采样点来估计待插点的属性值。该方法在数学上可对研究的对象提供一种最佳线性无偏估计（某点处的确定值），它在考虑了信息样品的形状、大小、与待估计块段之间的空间位置等几何特征以及品位的空间结构之后，为达到线性、无偏和最小估计方差的估计，对每一个样品赋予一定的系数，最后进行加权平均来估计块段品位。其基本插值步骤如下。

步骤1 计算半方差，衡量各点之间的空间相关程度，其计算式为：

其中，h为各监测之间的距离，n为由h分开的成对样本的数量，z(xi)为点xi的属性值。

步骤2 建立空间变异函数，将不同距离的半方差值都计算出来后，找出与之拟合得最好的理论变异函数模型，可用于拟合的模型包括高斯模型、线性模型、指数模型等。

步骤3 利用拟合的模型估算未知点的属性值，计算式为：

其中，z0为未标记样本的AQI估计值，zxi为标记样本点xi的AQI值，s为用来估算未知点的已知样本点的数目，λxi为在估计z0时的zxi的权值系数。λxi由计算式（4）计算：

其中，γ(xi,xj)为已知样本点 xi和 xj之间的变异函数值，μ为拉格朗日常数，γ(xi,x)为未知样本点与其他已知样本点 xi之间的变异函数值。

4.2 ALK模型

4.2.1 主动学习

在使用一些传统的监督学习方法训练模型的时候，往往是训练样本规模越大，模型的效果就越好。但在现实生活的很多场景中，标记样本的获取是比较困难的，这需要领域内的专家进行人工标注，时间成本和经济成本都很大。而且，如果训练样本的规模过于庞大，训练时间也会比较长。在人类的学习过程中，通常利用已有的经验学习新的知识，同时依靠获得的知识总结和积累经验，经验与知识不断交互。机器学习模拟人类学习的过程，利用已有的知识训练出模型，获取新的知识，并通过不断积累的信息修正模型，以得到更加准确、有用的新模型。因此，本文根据主动学习算法获得需要进行标注的数据，之后将这些数据送到专家那里进行标注，再将这些数据加入训练样本集中对模型进行训练，以提高模型的精确度。这个过程叫作主动学习。

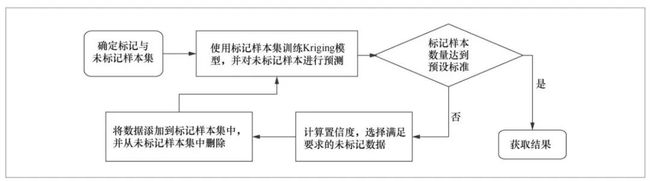
主动学习在每一轮的训练过程中反复运用监督学习方法，得到上一轮标记结果中最有价值的样例，并主动采样其真实标签，将结果一起加入当前的训练样本集中，不断训练。本文将主动学习理论应用于克里金插值模型，得到基于主动学习的克里金插值模型。ALK算法流程如图2所示，步骤如下。

图2 基于主动学习的克里金模型算法流程

步骤1 确定标记与未标记样本集，初始化克里金插值模型参数，本文克里金插值模型采用指数函数。

步骤2 使用标记样本训练克里金模型，并对未标记样本集进行插值估算。

步骤3 从插值结果中选择满足置信度要求的未标记样本及其主动采样获得的真实标签，将加入插值模型的标记样本集中，并从未标记样本集中去除该样本。

步骤4 重新训练克里金插值模型，直至训练出一定数量的未标记样本为止。

4.2.2 基于置信度的计算方法

在基于置信度的主动学习算法中，置信度被用于从若干未标记样本中选取最有价值的训练结果，在模型学习过程中，每一轮选取的未标记样本都会对插值模型的精度产生影响，在主动学习中，选定的最有价值的未标记样本会主动标记真实标签，因此通常选择模型学习中最不确定的未标记样本，因为它对学习模型来说是最有价值的。本文采用了Kriging模型中的均方差（mean-square error，MSE）作为置信度评判的指标，考虑了以下两种置信度计算方法。

● MSE1-MSE2：如果在未标记样本中存在一条数据，当其加入标记样本时，使得插值模型的均方差变大且变大的幅度最大或使插值模型的均方差变小且变小的幅度最小，则这条数据为置信度最低的未标记样本，置信度V使用以下计算式计算：

其中，yi是第 i个标记在原插值模型上的MSE，yˆi是第i个标记样本在新插值模型上的 MSE，这里的新插值模型指的是加入一条未标记样本后训练的模型，加入的未标记样本的标签是由原插值模型预测的结果。当V最小时，此未标记样本为本次循环中置信度最低的样本。

● MSE：直接选择ALK模型对未标记样本的预估值与实际值误差最大的点为置信度最低的未标记样本。

5 实验结果

在这一部分中，首先对数据集进行了描述。然后，评估本文提出的ALK模型的性能。最后，展示了该模型应用于空气质量指数预测的结果。

5.1 数据描述

在这项研究中，主要使用空气质量数据。数据集包含从2014年5月到2015年4月43个城市共437个空气监测站的空气质量数据，每条空气质量数据包含特定时间各个污染物浓度的信息。表2为数据集中某空气监测站的空气质量记录，其中station_id是空气监测站的ID，time是该条空气质量监测的时间，其余分别为PM2.5、PM10、NO2、CO、O3、SO2的浓度信息。本文主要关注空气质量指数，因此从空气质量数据中提取除CO之外的5种污染物浓度信息，并计算AQI。

表3为某空气监测站的数据，其中station_id是空气监测站的ID，name_chinese、name_english分别为空气监测站的中文名称与英文名称，latitude、longitude分别为空气监测站的经度和纬度，district_id为监测站 对应的街道ID。需要从空气监测站记录数据中提取空间位置信息，用于训练模型。对监测站点的纬度和经度使用聚类算法，将437个站点分为两个簇（簇1和簇2），然后将整合提取到的所有特征用于训练模型。

5.2 评估指标

本文实验将监测站点随机分为两组（标记样本集与未标记样本集），分别使用克里金插值、基于主动学习的克里金插值和普通机器学习回归树方法对未标记站点集进行空间插值分析。为了验证模型精 度，通过平均绝对百分误差（MAPE）对插值结果进行评估。MAPE值越小，代表模型的精度越高，其计算式如下：

本文采用了以下两种方法计算MAPE。

● 方法一：直接采用测试数据计算MAPE。

● 方法二：将每个簇整个空间划分为40×40的网格，对每个格子进行插值，选取与测试点最近的格子，计算MAPE。

本实验选取一天24 h的数据，使用传统的克里金插值建模，并对数据进行测试，测试结果如图3、图4所示。结果表明，方法一和方法二的预测误差相差不大，因此两种方法预测出的结果可以相互验证，接下来实验将选用方法一计算误差。

图3 簇1两种计算误差方法对比

图4 簇2两种计算误差方法对比

5.3 置信度计算方法选择

本节首先对MSE1-MSE2和MSE两种置信度计算方法进行对比，之后选择结果更 优的置信度计算方法指 导采样训练ALK模型，并与随机采样的Kriging模型进行比较。本实验还将流形适应实验设计（manifold adaptive experimental design，MAED）主动学习算法与克里金插值和传统机器学习方法回归树结合，训练模型。

如图5、图6所示，分别使用两种基于置信度的计算方法建立ALK模型，实验结果表明，用MSE方法训练的克里金模型的误差更低，因此之后的研究中使用此方法训练克里金模型，并进行比较。

图5 簇1基于置信度的两种计算方法对比

图6 簇2基于置信度的两种计算方法对比

5.4 模型性能结果

首先，对于模型性能，本实验将数据集中25%的随机子集作为测试集，模型在剩余75%的数据集中进行训练，训练集分为两部分，一部分是已知AQI的，一部分是未知、等待抽样的。预测AQI的目标是估计一个地区在时间窗内的空气质量的变化，而这种变化不能被直接地观测到。因此，在每个时间段中训练模型，得到空气质量指数的估计值，然后将估计值与测试数据进行比较。

当规定20个采样点时，结果表明ALK模型所选样本对空间的覆盖率更大，可以更好地对空间数据进行插值。

均方根误差（RMSE）是一种常用的测量模型预测值和实际观察值的差值的方法。经计算，使用克里金插值法与基于主动学习的Kriging插值法的插值精度提升对比见表4。由表4可知，基于主动学习的克里金插值相对于传统的克里金插值性能有所提升。前者使用主动学习算法主动采样预测结果最差的未标记样本的正确标签，由于该样本对学习模型来说是最有价值的，因此将这条数据加入训练集后可以使模型更好地学习，从而提高精确度。

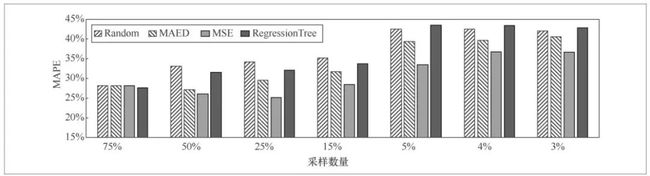
以克里金插值为基础数据推测算法， 3种采样算法对模型性能的改善如图7、图8所示，相对于随机采样算法（Random）， MAED主动采样算法并没有明显提升模型性能且结果不稳定，而笔者提出的以MSE为评估指标的主动采样算法则可以稳定地提升预测精度。由于MAED算法选取的监测站点不一定有数据，因此当采样数量少时，MAED算法选择的有数据的样本数可能达不到训练模型要求的样本数，因此在图7中最右侧该结果为空。

图7 簇1不同标记样本数量的预测结果

图8 簇2不同标记样本数量的预测结果

当标记数据数量少，未标记数量多时，以MSE为评估指标的主动采样算法的预测精度更优，如图9、图10所示，在相同误差下，以MSE为评估指标的主动采样算法需要的样本点明显少于随机采样算法。此外，还将本文提出的算法与普通机器学习回归树算法（RegressionTree)进行了比较，结果表明，以MSE为评估指标的主动采样算法使用最少且最有价值的数据达到了更好的预测结果，节约了人工标记数据的经济成本与时间成本。

图9 簇1相同误差下所需的标记样本数

图10 簇2相同误差下所需的标记样本数

6 结束语

本文研究了如何利用已有的空气质量数据、监测站点数据预测指定位置的空气质量指数。笔者提出了基于主动学习的克里金插值模型，在只有少量标记样本时，该模型可以有效地提高克里金插值法的预测精度。实际数据的实验结果表明，笔者提出的模型比传统方法更有效。本文未考虑气象等因素对空气质量指数的影响，未来不仅要对插值方法进行深入研究，还要考虑时间自相关 性以及跨域数据等因素，以进一步提高插值精度。

The authors have declared that no competing interests exist. 

作者已声明无竞争性利益关系。

作者简介

常慧娟（1995-），女，西北工业大学计算机学院硕士生，主要研究方向为群智感知。

於志文（1977-），男，博士，西北工业大学计算机学院教授，中国计算机学会（CCF）高级会员，主要研究方向为普适计算、社会感知计算。

於志勇（1982-），男，博士，福州大学数学与计算机科学学院副教授，CCF会员，主要研究方向为普适计算、移动社交网络。

安琦（1993-），女，西北工业大学计算机学院硕士生，CCF学生会员，主要研究方向为群智感知。

郭斌（1980-），男，博士，西北工业大学计算机学院教授，CCF高级会员，主要研究方向为普适计算、移动群智感知。

《大数据》期刊

《大数据（Big Data Research，BDR）》双月刊是由中华人民共和国工业和信息化部主管，人民邮电出版社主办，中国计算机学会大数据专家委员会学术指导，北京信通传媒有限责任公司出版的中文科技核心期刊。

关注《大数据》期刊微信公众号，获取更多内容

---

往期文章回顾

专题导读：新工科背景下的大数据人才培养及课程体系设计

“数据科学”课程群与  “数据科学导论”课程建设初探

大数据技术原理与应用课程建设经验分享

新工科背景下大数据专业导论课程的改革与探索

新工科背景下的计算机类专业人才培养探讨

---