利用matlab实现DMD动态模态分解(在一维信号或二维流场矢量中的应用)
利用matlab实现DMD动态模态分解(在一维信号或二维流场矢量中的应用)
- 0 前言
-
- 0.1 特征根的计算与含义
- 1 DMD的基本思路
- 2 一维DMD算法
- 3 二维DMD算法
- 4 总结
(2020年9月更新1,增加了第二章对于DMD模态排序的方法介绍。另外增加了一个注释:%旧版本matlab可以用右边形式替换Time_DMD=(b*ones(1,N)).*Q;。 由于旧版本中的 . ∗ .* .∗不支持向量和矩阵之间的操作,所以特此注释。如果代码中还有类似的报错,请参照前面提到的方法进行自行修改即可。)
0 前言
DMD的全称为Dynamic Mode Decomposition,译为动态模态分解,是一种常见的数据降维方法,本文主要是尝试利用matlab对DMD方法进行实现。
本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。
本文只代表个人的理解,如果有描述不准确或者错误的地方,欢迎在评论区指正。
期间涉及到一些POD分解与SVD分解的相关知识,建议先阅读下面这篇文章(自引):
【利用matlab实现POD分解(在一维信号或二维流场矢量中的应用)】
文章利用到的参考文献如下:
[1]Modal Analysis of Fluid Flows: An Overview(Kunihiko Taira、Steven L. Brunton等人)
[2]Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems(J. Nathan Kutz,Steven L. Brunton等人)
0.1 特征根的计算与含义
matlab中特征值和特征向量都可以用eig()函数进行计算。
[V,D] = eig(A)
其中V为特征向量组成的矩阵,D为特征根所组成的矩阵。A、V和D三个矩阵之间的关系为:A* V = V* D。
其中V的每一列都为一个特征向量,特征值对应的D矩阵中对角线上的相应列。
从线性变换的角度来看,矩阵的特征根和特征向量代表了变换的大小和方向。
当特征值为实数时,大于1代表变换的增长,小于1代表变换的缩小,特征向量代表变换的方向。以矩阵A=[0.95,-0.35;-0.35,0.95]为例,其特征值为0.6和1.3,特征向量的方向一个为45度,一个-45°。矩阵A对于随机点阵的效果如下所示。可以看到在经过矩阵A相乘后,随机点阵发生了变形,变形的方向就是特征向量的方向,变形的大小就是特征根的大小。大于1的方向拉长,小于1的方向缩短。

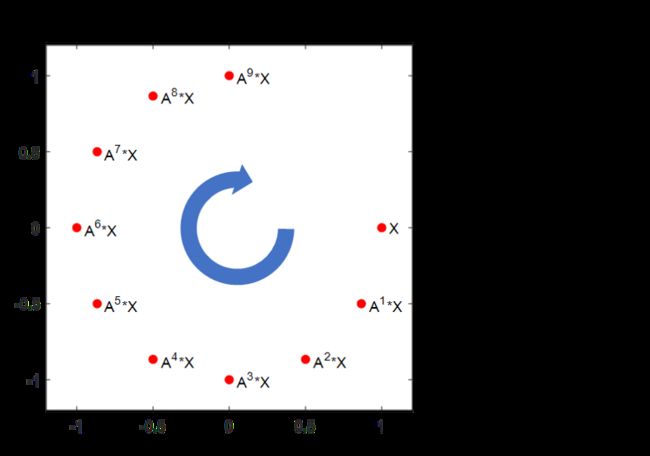
当特征值为复数时,则代表旋转。以A=[0.866,0.5;-0.5,0.866]为例,特征值为 cos30° ± sin30° * i ,每次乘以矩阵A代表旋转30度(当然我这里为了作图好看,通过调整特征向量把图形变为正圆,一般情况是一个椭圆)。
1 DMD的基本思路
DMD分解的基本思想就是线性变换。比如定义一个信号Utx,x为一维信号上每一点的数值,t为随时间变化下,整个信号的变化。时间采样点为N个,空间采样点为m个。Utx的转置矩阵为Uxt。
U t x = [ u ( t 1 , x 1 ) u ( t 1 , x 2 ) ⋯ u ( t 1 , x m ) u ( t 2 , x 1 ) u ( t 2 , x 2 ) ⋯ u ( t 2 , x m ) ⋮ ⋮ ⋱ ⋮ u ( t N , x 1 ) u ( t N , x 2 ) ⋯ u ( t N , x m ) ] U_{tx}=\left[ \begin{matrix} u\left( t_1,x_1 \right)& u\left( t_1,x_2 \right)& \cdots& u\left( t_1,x_m \right)\\ u\left( t_2,x_1 \right)& u\left( t_2,x_2 \right)& \cdots& u\left( t_2,x_m \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( t_N,x_1 \right)& u\left( t_N,x_2 \right)& \cdots& u\left( t_N,x_m \right)\\ \end{matrix} \right] Utx=⎣⎢⎢⎢⎡u(t1,x1)u(t2,x1)⋮u(tN,x1)u(t1,x2)u(t2,x2)⋮u(tN,x2)⋯⋯⋱⋯u(t1,xm)u(t2,xm)⋮u(tN,xm)⎦⎥⎥⎥⎤
初始时刻t=1时,信号以列向量的形式可以记为Ux1:
U x 1 = [ u ( t 1 , x 1 ) u ( t 1 , x 2 ) ⋮ u ( t 1 , x m ) ] U_{x1}=\left[ \begin{matrix} u\left( t_1,x_1 \right) \\ u\left( t_1,x_2 \right)\\ \vdots\\ u\left( t_1,x_m \right)\\ \end{matrix} \right] Ux1=⎣⎢⎢⎢⎡u(t1,x1)u(t1,x2)⋮u(t1,xm)⎦⎥⎥⎥⎤
那么DMD方法认为,如果系统是一个线性系统,则我们可以找到一个矩阵A,使得:
U x 2 = A ∗ U x 1 U x 3 = A ∗ U x 2 = A 2 ∗ U x 1 U x 4 = A ∗ U x 3 = A 3 ∗ U x 1 U_{x2}=A*U_{x1} \\ U_{x3}=A*U_{x2}=A^{2}*U_{x1} \\ U_{x4}=A*U_{x3}=A^{3}*U_{x1} Ux2=A∗Ux1Ux3=A∗Ux2=A2∗Ux1Ux4=A∗Ux3=A3∗Ux1
因此,我们只要知道初始的状态Ux1,以及系统的变换矩阵A,就可以知道系统之后任意时刻t的状态UxN。对于某些非线性系统,也可以找到一个近似的矩阵A,用来进行数据降维处理,然而效果肯定比线性系统的效果差。
因此,DMD分解的目的,就是把系统进行线性变换的分解。第k个时间步信号Uxk可以经过DMD分解变为
U x , k = ∑ i = 1 m b i ⋅ λ i k ⋅ ϕ i U_{x,k} =\sum_{i=1}^m{b_i \cdot \lambda_{i}^{k} \cdot \phi _i} Ux,k=i=1∑mbi⋅λik⋅ϕi
其中b为初始值, λ \lambda λ为矩阵A的特征根, ϕ \phi ϕ为对应的模态。
其中特征根可以利用衰减率 μ \mu μ来替换:
λ = exp ( μ ⋅ Δ t ) \lambda=\exp(\mu \cdot \Delta t) λ=exp(μ⋅Δt)
我们也可以把离散步k转换为时间t的形式:
U x , t = ∑ i = 1 m b i ⋅ e μ i ⋅ t ⋅ ϕ i U_{x,t} =\sum_{i=1}^m{b_i \cdot e^{\mu_{i} \cdot t} \cdot \phi _i} Ux,t=i=1∑mbi⋅eμi⋅t⋅ϕi
所以综上所述,我们只要知道矩阵A和初始时刻Ux1,就可以知道系统之后任意时刻的状态。同时根据矩阵A的特征值,还可以得到系统的增长率和变化频率。
我们设矩阵X为第1步至第N-1步组成的矩阵:
X = U x , t ( 1 ⋯ N − 1 ) = [ u ( x 1 , t 1 ) u ( x 1 , t 2 ) ⋯ u ( x 1 , t N − 1 ) u ( x 2 , t 1 ) u ( x 2 , t 2 ) ⋯ u ( x 2 , t N − 1 ) ⋮ ⋮ ⋱ ⋮ u ( x m , t 1 ) u ( x m , t 2 ) ⋯ u ( x m , t N − 1 ) ] X=U_{x,t(1 \cdots N-1)}=\left[ \begin{matrix} u\left( x_1,t_1 \right)& u\left( x_1,t_2 \right)& \cdots& u\left( x_1,t_{N-1} \right)\\ u\left( x_2,t_1 \right)& u\left( x_2,t_2 \right)& \cdots& u\left( x_2,t_{N-1} \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( x_m,t_1 \right)& u\left( x_m,t_2 \right)& \cdots& u\left( x_m,t_{N-1} \right)\\ \end{matrix} \right] X=Ux,t(1⋯N−1)=⎣⎢⎢⎢⎡u(x1,t1)u(x2,t1)⋮u(xm,t1)u(x1,t2)u(x2,t2)⋮u(xm,t2)⋯⋯⋱⋯u(x1,tN−1)u(x2,tN−1)⋮u(xm,tN−1)⎦⎥⎥⎥⎤
我们设矩阵Y为第2步至第N步组成的矩阵:
Y = U x , t ( 2 ⋯ N ) = [ u ( x 1 , t 2 ) u ( x 1 , t 3 ) ⋯ u ( x 1 , t N ) u ( x 2 , t 2 ) u ( x 2 , t 3 ) ⋯ u ( x 2 , t N ) ⋮ ⋮ ⋱ ⋮ u ( x m , t 2 ) u ( x m , t 3 ) ⋯ u ( x m , t N ) ] Y=U_{x,t(2 \cdots N)}=\left[ \begin{matrix} u\left( x_1,t_2 \right)& u\left( x_1,t_3 \right)& \cdots& u\left( x_1,t_{N} \right)\\ u\left( x_2,t_2 \right)& u\left( x_2,t_3 \right)& \cdots& u\left( x_2,t_{N} \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( x_m,t_2 \right)& u\left( x_m,t_3 \right)& \cdots& u\left( x_m,t_{N} \right)\\ \end{matrix} \right] Y=Ux,t(2⋯N)=⎣⎢⎢⎢⎡u(x1,t2)u(x2,t2)⋮u(xm,t2)u(x1,t3)u(x2,t3)⋮u(xm,t3)⋯⋯⋱⋯u(x1,tN)u(x2,tN)⋮u(xm,tN)⎦⎥⎥⎥⎤
因为
U x , N = A ∗ U x , N − 1 U_{x,N}=A*U_{x,N-1} Ux,N=A∗Ux,N−1
所以
Y = A ∗ X Y=A*X Y=A∗X
矩阵A可以计算得到,其中pinv(X)代表矩阵X的伪逆(广义逆)。
A = Y ∗ p i n v ( X ) A=Y* pinv(X) A=Y∗pinv(X)
matlab演示如下:
%DMD实验2
clear
close all
x=0:0.01:5;m=length(x);
t=0:0.1:5;N=length(t);
Fs=1/(t(2)-t(1));
[X,T]=meshgrid(x,t);
%信号
U_tx=1.2*exp(-0.5*T).*sin(2*pi*(X+0*T))+0.8*exp(0.3*T).*sin(2*pi*(3*X+4*T));
%p的格式为时间*空间的矩阵
U_xt=U_tx';
Up=pinv(U_xt(:,1:50));%求解X的伪逆
%求解矩阵A
A=U_xt(:,2:51)*Up;
[V,D] = eig(A);
D=diag(D);
[~,ind] = sort(abs(D),'descend');
D=D(ind);V=V(:,ind);
D_abs=abs(D);
Dd=D./D_abs;
%频率
f=Fs*angle(Dd)./(2*pi);
%图1,绘制特征根图谱
figure(1)
scatter(real(Dd(100:-1:1)),imag(Dd(100:-1:1)),30,-abs(D(100:-1:1)),'filled')
axis equal
box on
%图2,绘制频率和衰减图
figure(2)
wa=log(D)*Fs;%利用特征根计算衰减率
scatter(real(wa),imag(wa)/2/pi,30,-D_abs,'filled')
xlabel('衰减率σ');ylabel('频率w')
ylim([-6,6]);xlim([-1,1])
hold on
plot([0,0],ylim,'b--')
plot(xlim,[0,0],'b--')
box on
信号为:
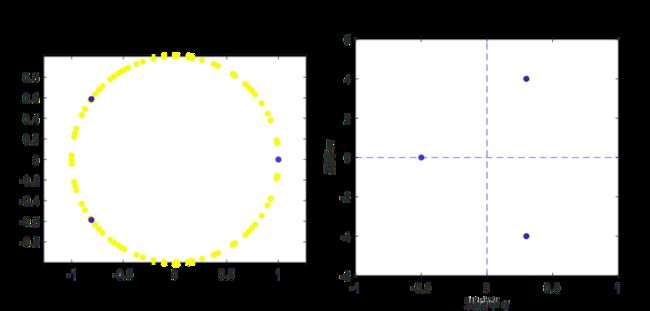
U ( T , X ) = 1.2 ⋅ e − 0.5 T sin ( 2 π X ) + 0.8 ⋅ e 0.3 T sin ( 2 π ( 3 X + 4 T ) ) U(T,X)=1.2 \cdot e^{-0.5 T}\sin(2\pi\ X)+0.8 \cdot e^{0.3 T} \sin(2\pi(3X+4T)) U(T,X)=1.2⋅e−0.5Tsin(2π X)+0.8⋅e0.3Tsin(2π(3X+4T))
矩阵A的特征根分布以及前3阶模态的衰减率如下。第一个模态衰减率为-0.5,频率为0。第二个和第3个模态(可以视为一对)衰减率为0.3,频率为4hz。希望可以用这个例子更好的去理解第0.1节和第1节中,矩阵A的特征值与衰减率、频率等之间的关系。
2 一维DMD算法
第1节虽然介绍了如何求解矩阵A,但是利用伪逆方法计算在计算量和结果稳定性上都有缺点,因此第1节的结果只是作为辅助理解DMD的基本思路。
之后介绍通用的DMD程序算法:
-
第1步,定义矩阵X和矩阵Y:
我们设矩阵X为第1步至第N-1步组成的矩阵:
X = U x , t ( 1 ⋯ N − 1 ) = [ u ( x 1 , t 1 ) u ( x 1 , t 2 ) ⋯ u ( x 1 , t N − 1 ) u ( x 2 , t 1 ) u ( x 2 , t 2 ) ⋯ u ( x 2 , t N − 1 ) ⋮ ⋮ ⋱ ⋮ u ( x m , t 1 ) u ( x m , t 2 ) ⋯ u ( x m , t N − 1 ) ] X=U_{x,t(1 \cdots N-1)}=\left[ \begin{matrix} u\left( x_1,t_1 \right)& u\left( x_1,t_2 \right)& \cdots& u\left( x_1,t_{N-1} \right)\\ u\left( x_2,t_1 \right)& u\left( x_2,t_2 \right)& \cdots& u\left( x_2,t_{N-1} \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( x_m,t_1 \right)& u\left( x_m,t_2 \right)& \cdots& u\left( x_m,t_{N-1} \right)\\ \end{matrix} \right] X=Ux,t(1⋯N−1)=⎣⎢⎢⎢⎡u(x1,t1)u(x2,t1)⋮u(xm,t1)u(x1,t2)u(x2,t2)⋮u(xm,t2)⋯⋯⋱⋯u(x1,tN−1)u(x2,tN−1)⋮u(xm,tN−1)⎦⎥⎥⎥⎤
我们设矩阵Y为第2步至第N步组成的矩阵:
Y = U x , t ( 2 ⋯ N ) = [ u ( x 1 , t 2 ) u ( x 1 , t 3 ) ⋯ u ( x 1 , t N ) u ( x 2 , t 2 ) u ( x 2 , t 3 ) ⋯ u ( x 2 , t N ) ⋮ ⋮ ⋱ ⋮ u ( x m , t 2 ) u ( x m , t 3 ) ⋯ u ( x m , t N ) ] Y=U_{x,t(2 \cdots N)}=\left[ \begin{matrix} u\left( x_1,t_2 \right)& u\left( x_1,t_3 \right)& \cdots& u\left( x_1,t_{N} \right)\\ u\left( x_2,t_2 \right)& u\left( x_2,t_3 \right)& \cdots& u\left( x_2,t_{N} \right)\\ \vdots& \vdots& \ddots& \vdots\\ u\left( x_m,t_2 \right)& u\left( x_m,t_3 \right)& \cdots& u\left( x_m,t_{N} \right)\\ \end{matrix} \right] Y=Ux,t(2⋯N)=⎣⎢⎢⎢⎡u(x1,t2)u(x2,t2)⋮u(xm,t2)u(x1,t3)u(x2,t3)⋮u(xm,t3)⋯⋯⋱⋯u(x1,tN)u(x2,tN)⋮u(xm,tN)⎦⎥⎥⎥⎤ -
第2步,对矩阵X进行svd分解
[ U , S , V ] = svd ( X ) \left[ U,S,V \right] =\text{svd}\left( X \right) [U,S,V]=svd(X) -
第3步,计算矩阵A
A = U ′ ∗ Y ∗ V ∗ S − 1 ; A=U'*Y*V*S^{-1}; A=U′∗Y∗V∗S−1; -
第4步,计算矩阵A的特征向量w和特征值 λ \lambda λ
[ ω , λ ] = eig ( A ) [\omega, \lambda]=\text{eig}\left( A \right) [ω,λ]=eig(A) -
第5步,计算DMD模态
这里模态 ϕ \phi ϕ可以用:
ϕ = U ∗ ω \phi=U*\omega ϕ=U∗ω
也有文献认为上面式子只用到了X的信息,没有用到Y的信息,所以把公式改进为:
ϕ = Y ∗ V ∗ S − 1 ∗ ω \phi=Y*V*S^{-1}*\omega ϕ=Y∗V∗S−1∗ω -
第6步,计算DMD模态对应的初始值b。第一步等价于信号的初始值Ux1。
ϕ ∗ b = U x 1 \phi*b=U_{x1} ϕ∗b=Ux1 -
第7步,对DMD模态进行排序。
这里可以直接利用第6步中提到的初始值进行排序。这种排序的优点是计算量小。但是考虑到信号会增长或衰减,所以这种排序的缺点是,容易把初始值特别大,但是衰减很快的模态(可能是噪声)放在前面,或者忽略初始值比较小,但是增长很快的信号。因此,还可以用信号的能量对模态进行排序。模态的能量被定义为,每一时刻、每一点振幅的平方和。每一时刻的的信号等于初始信号乘以特征值,可以计算为:
U x k = U x 1 ∗ λ k − 1 = ϕ ∗ b ∗ λ k − 1 U_{xk}=U_{x1}*\lambda^{k-1}=\phi*b*\lambda^{k-1} Uxk=Ux1∗λk−1=ϕ∗b∗λk−1
对于不同的模态,不同时间,我们可以利用范德蒙矩阵来储存特征值的变化,总共有m个特征值:
[ 1 λ 1 1 ⋯ λ 1 N − 1 1 λ 2 1 ⋯ λ 2 N − 1 ⋮ ⋮ ⋱ ⋮ 1 λ m 1 ⋯ λ m N − 1 ] \left[ \begin{matrix} 1& \lambda_{1}^{1}& \cdots& \lambda_{1}^{N-1}\\ 1& \lambda_{2}^{1}& \cdots& \lambda_{2}^{N-1}\\ \vdots& \vdots& \ddots& \vdots\\ 1& \lambda_{m}^{1}& \cdots& \lambda_{m}^{N-1}\\ \end{matrix} \right] ⎣⎢⎢⎢⎡11⋮1λ11λ21⋮λm1⋯⋯⋱⋯λ1N−1λ2N−1⋮λmN−1⎦⎥⎥⎥⎤
需要求第r个模态随时间变化的话,只需要提出范德蒙矩阵的一部分,然后利用下面公式进行求解即可。 λ r \lambda_{r} λr是第r个模态对应的特征根。
ϕ r ∗ b r ∗ [ 1 λ r 1 ⋯ λ r N − 1 ] \phi_{r}*b_{r}* \left[ \begin{matrix} 1& \lambda_{r}^{1}& \cdots& \lambda_{r}^{N-1}\\ \end{matrix} \right] ϕr∗br∗[1λr1⋯λrN−1]
之后得到了这个模态下,每一时刻每一位置组成的时间-空间矩阵。对矩阵每一个元素做平方,然后相加,定义为这个模态在整个时间段内的总能量。
之后,便是一些后处理,比如特征根分布图,各个模态的信号图,模态的衰减率和频率图,各个模态的频率-能量(振幅)图,等等。
matlab代码如下:
%一维信号DMD分解示意程序
clear
close all
x=0:0.01:5;m=length(x);%空间
t=0:0.05:5;N=length(t);%时间
Fs=1/(t(2)-t(1));%采样频率
[X,T]=meshgrid(x,t);
%创建信号,Utx的格式为时间*空间的矩阵
U_tx=1.2*exp(-0.5*T).*sin(2*pi*(X+2*T))+0.8*exp(0.3*T).*sin(2*pi*(3*X+4*T))+0.1*rand(N,m)+1.1;
%计算X和Y
U_xt=U_tx';
X=U_xt(:,1:end-1);
Y=U_xt(:,2:end);
%计算DMD
[Dd,b,Phi,Time_DMD,Energy]=DMD_CLASS(X,Y);
%之后全部是后处理
figure(1)
%图1,输出特征根分布
scatter(real(Dd(end:-1:1)),imag(Dd(end:-1:1)),30,-log(Energy(end:-1:1)),'filled')
axis equal
set(gcf,'position',[488 342 400 350])
figure(2)
%图2,绘制频率和衰减图
wa=log(Dd)*Fs;
scatter(real(wa(end:-1:1)),imag(wa(end:-1:1))/2/pi,30,-log(Energy(end:-1:1)),'filled')
xlabel('衰减率σ');ylabel('频率w')
ylim([-6,6]);xlim([-1,1])
hold on
plot([0,0],ylim,'b--')
plot(xlim,[0,0],'b--')
hold off
box on
set(gcf,'position',[488 342 400 350])
figure(3)
%图3,绘制频率-能量排序
Freq=imag(wa)/2/pi;
k=find(Freq>=0);
stem(Freq(k),log10(Energy(k)),'BaseValue',-6,'MarkerFaceColor','auto');
ylim([-6,6]);
xlim([-1,11])
set(gca,'YTickLabel',{'1e-6','1e-4','1e-2','0','1e2','1e4','1e6'},'YTick',[-6:2:6])
set(gca,'XTick',[0:2:10])
xlabel('频率hz');ylabel('能量')
figure(4)
%绘制模态
subplot(3,2,1)%总
U_x1=U_xt(:,1);
plot(x,U_x1);
xlim([0,5])
subplot(3,2,2)%一阶模态
Uxt_DMD_k=real(Phi(:,1) * Time_DMD(1,:));
plot(x,Uxt_DMD_k(:,1));
ylim([0,3]);xlim([0,5])
subplot(3,2,3)%二阶模态
Uxt_DMD_k=real(Phi(:,2) * Time_DMD(2,:));
plot(x,Uxt_DMD_k(:,1));
xlim([0,5])
subplot(3,2,4)%三阶模态
Uxt_DMD_k=real(Phi(:,3) * Time_DMD(3,:));
plot(x,Uxt_DMD_k(:,1));
xlim([0,5])
subplot(3,2,5)%四阶模态
Uxt_DMD_k=real(Phi(:,4) * Time_DMD(4,:));
plot(x,Uxt_DMD_k(:,1));
xlim([0,5])
subplot(3,2,6)%五阶模态
Uxt_DMD_k=real(Phi(:,5) * Time_DMD(5,:));
plot(x,Uxt_DMD_k(:,1));
xlim([0,5])
figure(5)
%绘制前10阶模态能量占比
Cumsum_Energy=cumsum(Energy);
subplot(2,1,1)
bar( 1:10 , Cumsum_Energy(1:10)/Cumsum_Energy(end) ,'BarWidth',1)
ylim([0,1]);
subplot(2,1,2)
plot( 1:10 , Energy(1:10)/Cumsum_Energy(end) ,'-o')
ylim([0,1]);
figure(6)
%还原信号与原信号对比(利用前5阶模态还原)
Uxt_DMD_k=real(Phi(:,1:5) * Time_DMD(1:5,:));
plot(x,U_xt(:,1),x,Uxt_DMD_k(:,1))
function [Dd,b,Phi,Time_DMD,Energy]=DMD_CLASS(X,Y)
%DMD分解函数
%输入:
%X,Y,DMD分解的数据矩阵
%
%输出:
%Dd,特征根
%b,初始状态
%Phi,DMD分解的模态
%Time_DMD,DMD还原信号所用到的时间项
%Energy,每个模态对应的能量,从大到小排序
N=size(X,2);
%1 SVD分解
[U,S,V] = svd(X,'econ');
%删除奇异值约等于0的模态,防止计算发散
Sd=diag(S);
r=sum(Sd>1e-6);
U=U(:,1:r);
S=S(1:r,1:r);
V=V(:,1:r);
%2 求解矩阵A
A=U'*(Y*V/S);
%3 求矩阵A的特征值和特征向量
[Om,D]=eig(A);
Dd=diag(D);%求特征值转为向量形式
%4 求DMD模态
Phi=Y*V/S*Om;
%5 求解初始状态b
b=Phi\X(:,1);
%6 对模态进行排序
Q=Dd.^(0:N-1);%计算出范德蒙矩阵
Time_DMD=b.*Q;%旧版本matlab可以用右边形式替换Time_DMD=(b*ones(1,N)).*Q;
% %对信号初始振幅排序,速度快,输出能量可以近似用振幅平方代替
% [b,Ib] = sort(abs(b),'descend');
%求出所有模态的信号,并计算能量
Energy=zeros(size(Phi,2),1);
for k=1:size(Phi,2)
Uxt_DMD_k=real(Phi(:,k) * Time_DMD(k,:));
E_k=sum(sum(Uxt_DMD_k.^2));
Energy(k)=E_k;
end
[Energy,Ie] = sort(Energy,'descend');%对每个模态的能量进行排序
%按顺序输出特征值、初始状态b、模态Phi
Dd=Dd(Ie);
b=b(Ie);
Phi=Phi(:,Ie);
Time_DMD=Time_DMD(Ie,:);
end
输入信号为:
U ( T , X ) = 1.2 ⋅ e − 0.5 T sin ( 2 π ( X + 2 T ) ) + 0.8 ⋅ e 0.3 T sin ( 2 π ( 3 X + 4 T ) ) + 1.1 + n o i s e U(T,X)=1.2 \cdot e^{-0.5 T}\sin(2\pi\ (X+2T))+0.8 \cdot e^{0.3 T} \sin(2\pi(3X+4T))+1.1+noise U(T,X)=1.2⋅e−0.5Tsin(2π (X+2T))+0.8⋅e0.3Tsin(2π(3X+4T))+1.1+noise
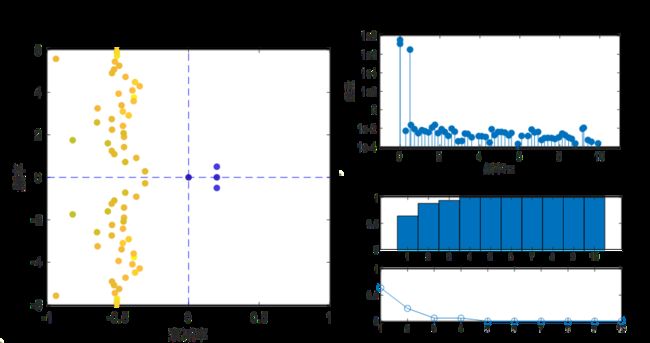
第一个信号空间频率1hz,时间频率为2hz,衰减率-0.5。第二个信号空间频率3hz,时间频率4hz,衰减率0.3。此外还加上了常数为1.1,加入了振幅为0.1的噪声。

特征根分布基本在一个圆上。其中,能量大的模态颜色深,能量小的模态颜色浅。
衰减率和频率图上,可以清晰的看到前5阶模态对应的位置,其中坐标原点上的是常数项,剩下4个点分别对应为4hz和2hz。
频率-能量图上,可以看到不同频率下信号的能量大小,其中0hz、2hz、4hz三个信号占比最大,对应了原始信号的输入。
能量占比上,上面的图可以看到前5阶信号能量几乎占到了100%,下面的图则展示了每一模态的能量。

之后,展示了每一阶模态的形态,可以看到DMD方法成功的将原本的混合信号,分离为各个模态。

将前5阶模态叠加,可以看到原始数据只用前5阶模态,便能较好的还原,实现了数据压缩。虽然与原始信号有一定差异,但这是加入了随机高频噪声导致的。
3 二维DMD算法
与一维DMD算法一样,把二维信号中的空间维度压缩为一个维度,然后再调用一维DMD算法即可。(这属于时间分解。还有一些地方用到了空间分解,不是沿着时间t维度分解,而是沿着空间维度进行分解,这里只是提及,不再进行尝试了。)
matlab算法如下:
%自己试一试DMD
clear
close all
%定义流场时间和空间信息
x=-8:0.2:8;
y=-5:0.2:5;
t=0:0.05:6;
Fs=1/(t(2)-t(1));
[X,Y,T]=meshgrid(x,y,t);
[Ny,Nx,Nt]=size(X);
%自定义流场,U是沿x方向的速度分量,V是y方向的
U0=-1*Y.^2+5;
V0=0*Y;%UV0不随时间变化,设为定常流场
U1=-5*sin(Y).*cos(2*pi*0.3*Y).*(exp(T/5));
V1=5*sin(X-1*pi*T).*cos(2*pi*0.3*Y).*(exp(T/5));
U3=0.01*rand(Ny,Nx,Nt);
V3=0.01*rand(Ny,Nx,Nt);
U_Sum=U0+U1+U3;
V_Sum=V0+V1+V3;
%1计算UV向量
U_xt=Uxyt_to_Uxt(U_Sum);%把2维问题转化为1维问题
V_xt=Uxyt_to_Uxt(V_Sum);%把2维问题转化为1维问题
%然后把UV向量合并
UV_xt=[U_xt;V_xt];
%之前的这些都属于数据准备和整理部分
%计算X和Y
UX=UV_xt(:,1:end-1);
UY=UV_xt(:,2:end);
%计算DMD
[Dd,b,Phi,Time_DMD,Energy]=DMD_CLASS(UX,UY);
%后处理
figure(1)
%图1,绘制频率和衰减图
wa=log(Dd)*Fs;
scatter(real(wa(end:-1:1)),imag(wa(end:-1:1))/2/pi,30,-log(Energy(end:-1:1)),'filled')
xlabel('衰减率');ylabel('频率')
ylim([-6,6]);xlim([-1,1])
hold on
plot([0,0],ylim,'b--')
plot(xlim,[0,0],'b--')
hold off
box on
set(gcf,'position',[488 342 400 350])
figure(2)
%图3,绘制频率-能量排序
Freq=imag(wa)/2/pi;
k=find(Freq>=0);
stem(Freq(k),log10(Energy(k)),'BaseValue',-4,'MarkerFaceColor','auto');
ylim([-4,8]);
xlim([-1,11])
set(gca,'YTickLabel',{'1e-4','1e-2','0','1e2','1e4','1e6','1e8'},'YTick',[-4:2:8])
set(gca,'XTick',[0:2:10])
xlabel('频率hz');ylabel('能量')
figure(3)
%绘制前10阶模态能量占比
Cumsum_Energy=cumsum(Energy);
subplot(2,1,1)
bar( 1:10 , Cumsum_Energy(1:10)/Cumsum_Energy(end) ,'BarWidth',1)
ylim([0,1]);
subplot(2,1,2)
plot( 1:10 , Energy(1:10)/Cumsum_Energy(end) ,'-o')
ylim([0,1]);
figure(4)
X=X(:,:,1);
Y=Y(:,:,1);
k=1;
%绘制模态
subplot(2,2,1)%总
[Uxy0,Vxy0]=UV2UxyVxy(UV_xt(:,k),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxy0,Vxy0));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxy0(1:5:end,1:5:end),Vxy0(1:5:end,1:5:end),'color','k')
hold off
axis equal off
title('总')
subplot(2,2,2)%1
UVxt_DMD_k=real(Phi(:,1) * Time_DMD(1,:));
[Uxyk,Vxyk]=UV2UxyVxy(UVxt_DMD_k(:,k),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxyk,Vxyk));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxyk(1:5:end,1:5:end),Vxyk(1:5:end,1:5:end),'color','k')
hold off
axis equal off
title('1阶')
subplot(2,2,3)%2
UVxt_DMD_k=real(Phi(:,2) * Time_DMD(2,:));
[Uxyk,Vxyk]=UV2UxyVxy(UVxt_DMD_k(:,k),Ny,Nx);
hold on
pcolor(X,Y,curl(X,Y,Uxyk,Vxyk));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxyk(1:5:end,1:5:end),Vxyk(1:5:end,1:5:end),'color','k')
hold off
axis equal off
title('2阶')
subplot(2,2,4)%3&4
UVxt_DMD_k=real(Phi(:,3) * Time_DMD(3,:));
[Uxy3,Vxy3]=UV2UxyVxy(UVxt_DMD_k(:,k),Ny,Nx);
UVxt_DMD_k=real(Phi(:,4) * Time_DMD(4,:));
[Uxy4,Vxy4]=UV2UxyVxy(UVxt_DMD_k(:,k),Ny,Nx);
Uxyk=Uxy3+Uxy4;
Vxyk=Vxy3+Vxy4;
hold on
pcolor(X,Y,curl(X,Y,Uxyk,Vxyk));shading interp
quiver(X(1:5:end,1:5:end),Y(1:5:end,1:5:end),Uxyk(1:5:end,1:5:end),Vxyk(1:5:end,1:5:end),'color','k')
hold off
axis equal off
title('3+4阶')
function [Dd,b,Phi,Time_DMD,Energy]=DMD_CLASS(X,Y)
%DMD分解函数
%输入:
%X,Y,DMD分解的数据矩阵
%
%输出:
%Dd,特征根
%b,初始状态
%Phi,DMD分解的模态
%Time_DMD,DMD还原信号所用到的时间项
%Energy,每个模态对应的能量,从大到小排序
N=size(X,2);
%1 SVD分解
[U,S,V] = svd(X,'econ');
%删除奇异值约等于0的模态,防止计算发散
Sd=diag(S);
r=sum(Sd>1e-6);
U=U(:,1:r);
S=S(1:r,1:r);
V=V(:,1:r);
%2 求解矩阵A
A=U'*(Y*V/S);
%3 求矩阵A的特征值和特征向量
[Om,D]=eig(A);
%4 求DMD模态
Phi=Y*V/S*Om;
Dd=diag(D);%求特征值转为向量形式
%5 求解初始状态b
b=Phi\X(:,1);
Q=Dd.^(0:N-1);%计算出范德蒙矩阵
Time_DMD=b.*Q;%旧版本matlab可以用右边形式替换Time_DMD=(b*ones(1,N)).*Q;
% %对信号初始振幅排序,速度快
% [~,Ib] = sort(abs(b),'descend');
%求出所有模态的信号,并计算能量
Energy=zeros(size(Phi,2),1);
for k=1:size(Phi,2)
Uxt_DMD_k=real(Phi(:,k) * Time_DMD(k,:));
E_k=sum(sum(Uxt_DMD_k.^2));
Energy(k)=E_k;
end
[Energy,Ie] = sort(Energy,'descend');%对每个模态的能量进行排序
%按顺序输出特征值、初始状态b、模态Phi
Dd=Dd(Ie);
b=b(Ie);
Phi=Phi(:,Ie);
Time_DMD=Time_DMD(Ie,:);
end
function Uxt=Uxyt_to_Uxt(Uxyt)
%把3维矩阵的xyt压缩为xt
[Ny,Nx,Nt]=size(Uxyt);%这里是matlab的meshgrid定义导致的,x和y是反着的,注意。
Nxy=Ny*Nx;
Uxt=reshape(Uxyt,Nxy,Nt);
end
function [Uxy,Vxy]=UV2UxyVxy(UVx,Ny,Nx)
Ux=UVx(1:Ny*Nx);
Vx=UVx(Ny*Nx+1:end);
Uxy=reshape(Ux,Ny,Nx);
Vxy=reshape(Vx,Ny,Nx);
end
计算的结果如下:
可以从图中读出,流场可以分解为一个恒定场,一个衰减率0.2的恒定场,和一对0.2的衰减率,和0.5hz的频率运动的场组成。这4个模态占据了整个流场接近100%的能量。
分解的模态如下图所示(GIf选取的循环时间比较短,所以看不出明显的衰减行为)。

4 总结
DMD算法属于数据驱动算法,输入的量只有数据,不依赖于其它因素。而且对于线性系统,DMD可以分离出不同频率与衰减率的模态,而且还可以预测线性系统未来的变化,这是POD无法比拟的。当然,DMD的优势在于线性系统,对于非线性系统(不满足Y=AX),DMD的结论可信度就会下降,或者说只能给出类似于线性的近似结果。
但是由于其思想的限制,DMD算法对数据的排序非常敏感,如果颠倒顺序或者缺少数据,就无法得到正确的变换矩阵A。所以和POD相比,DMD只能用在采样频率比较高的数据上,而且对数据的连续性、采样频率的恒定性等方面有很高的要求。而且与POD相比,DMD对噪声也更为敏感。为了克服这些缺点,DMD也衍生出很多变体,有兴趣的话可以自己去查文献。