机器学习：基于python的KNN算法实现

介绍KNN之前，我们先通过一段代码来看组数据

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import seaborn as sns

data = make_blobs(n_samples=300, centers=3, random_state=10)
x, y = data
sns.set()
plt.scatter(x[:, 0],x[:, 1],c=y, cmap=plt.cm.spring, edgecolor='k')
plt.plot(2.75, 3, 'b*',markersize=13)
plt.show()

图中红色箭头指向的五角星，是一个未知分类的点（2.75，3），而从图中已知分类的点，可以看出点分成三类：红、黄、紫。如果问，这个五角星最有可能归属哪个类，很容易会猜测红色，因为它似乎是在红色的类里面，但这种依据经验的说法显然是缺乏说服力的，我们需要一个更严谨的说法去下定义。

因为五角星的四周，即与五角星距离最近的几个点，绝大多数是红色的（相邻点的个数取决于五角星为中心的搜索半径的大小），我们是根据附近点来对其做一个预测，这就是KNN算法大概的思维方式。

k-近邻算法（K-Nearest Neighbors, KNN）属于有监督学习的范畴，通过现有的训练数据集进行建模，再用模型对新的数据样本进行分类或者回归分析。如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。前期的学习中KNN更多被用来打标（分类）。

《机器学习实战》这本书中提到，k-近邻算法的优点在在于：

1. 精度高
2. 对异常值不敏感（仅对近邻数据作判断）
3. 无数据输入假定

而因其属于惰性算法，也有以下缺点：

1. 计算复杂度高
2. 空间复杂度高
3. 可解释性差

在模型未优化的前提下，对大量数据测定距离是既耗时又耗力的，所以需要更多的优化方案去弥补KNN的不足，我会在以后谈及它的优化。

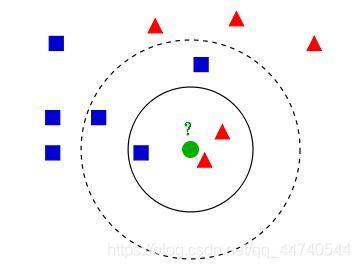
如上图，现在在空间中有两种数据：方形和三角，而圆形的预测样本现在暂时不知道归属于哪个类。如果以实线圆的范围来界定距离预测样本最近的几个点，那么实线圆内有三个测试样本，1个方形，2个三角，根据定义，三角数量较多，那么对预测样本的估计就是三角了；而如果以虚线圆的范围界定的话，圆内就有了5个测试样本，并且方形数量占优，预测样本会被归为方形。我们看到，前后预测出来的结果是不一致的，预测范围的不同会影响最终结果，这取决于用户给予KNN的权重K。

代码实现

我们可以先导入一份训练集，这里用的是比较出名的鸢尾花（iris）数据集，可以从sklearn库调用或者在UCI上下载，以下是sklearn库调用iris数据集的代码，以及之后需要用到的库，
UCI下载链接：http://archive.ics.uci.edu/ml/datasets/Iris

from sklearn import datasets
import numpy as np
import operator
import pandas as pd

iris = datasets.load_iris()
# iris_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
x = iris.data
y = iris.target

因为之前笔者处理的是UCI上的iris数据集，并且使用DataFrame保存数据，所以代码沿用到这篇博客中。读取iris数据集有多种方式，可以根据自己的喜好去选择。

# 使用 pd.DataFrame 读取
def getIris():
	data = pd.read_csv('iris.data')
	irisTemp = pd.DataFrame(columns = data.columns)
	irisTemp.loc[0]= data.columns
	iris = pd.concat([irisTemp,data])
	iris.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'class']
	iris.index = range(150)
	print(iris.head(5))
	return iris

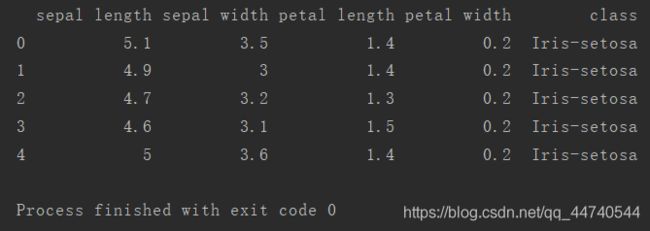
iris数据集中存储了鸢尾花的萼片长度、萼片宽度、花瓣长度、花瓣宽度与分类（Setosa、Versicolour、Virginica）更多关于iris Data Set的描述可以到UCI查看。

建立模型

KNN的工作原理是：存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前k个最相似的数据，通常k是不大于20的整数，最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

需要解决的问题：

• 计算样本距离
• 设计分类器（选择k个最相似数据）
• 完成测试算法（计算错误率）

下面我们分别讨论这三个问题。

计算样本距离

预测数据与样本数据之间的相关性，我们通过两者间的距离来衡量，距离近的比距离远的相关性强。计算距离的方法有很多种，这里列出较常用的两种

• 欧几里得度量（ Euclidean Distance ）
  欧式距离源自N维欧氏空间中两点$x_1$，$x_2$：
  
• 曼哈顿距离（ Manhattan distance ）
  又被称作出租车几何，用以标明两个点在标准坐标系上的绝对轴距总和

绿色线表示的是欧几里得距离，而其他红、蓝、黄色线表示的是曼哈顿距离

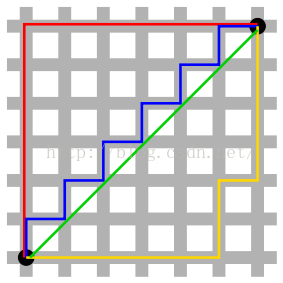
其他距离还有以下几个，这里不做扩展

• 切比雪夫距离 ( Chebyshev Distance )
• 闵可夫斯基距离( Minkowski Distance )
• 标准化欧氏距离 (Standardized Euclidean distance )
• 马氏距离(Mahalanobis Distance)
• 夹角余弦(Cosine)
• 汉明距离(Hamming distance)

我们用欧几里得度量来对样本距离做一个计算（二选一即可）

#计算欧式距离 ( DataFrame data )
def distEclud(point1, point2, length):
    distance = 0
    for x in range(length):
        distance += np.power(point1[x] - point2[x], 2)
    return np.sqrt(distance)

#计算欧式距离 ( matrix data )
def distEclud(vec1,vec2):
    return np.sum(np.power(vec1-vec2,2),axis=1)

分类器

调用距离计算函数实现对预测数据的预测，分类器classifier需要一个数据集和一个测试集，通过用户给定的k值的大小预测出测试集分类。

def classifier(dataSet, forecastSet, k):
    length = len(forecastSet[0]) - 1    #除去标签后的样本长度
    responses = []
    #测试集样本逐个测试
    for i in range(forecastSet.shape[0]):
        distances = []
        #训练集样本逐个求距离
        for x in range(dataSet.shape[0]):
            dist = distEclud(dataSet[x], forecastSet[i], length)
            distances.append((dataSet[x], dist))
        distances.sort(key=operator.itemgetter(1))      #根据距离dist排序
        neighbors = []
        #距离最小的前k个样本
        for x in range(k):
            neighbors.append(distances[x][0])
        count = {}
        #统计前k个样本的分类
        for x in range(len(neighbors)):
            response = neighbors[x][-1]
            if response in count:
                count[response] += 1
            else:
                count[response] = 1
        #返回k个样本中出现标签次数最多的分类
        Max = max(list(count.values()))
        responses.append(list(count.keys())[list(count.values()).index(Max)])       #根据字典values索引得到keys
    return responses

数据归一化

归一化是一种 “简易” 的加权方式。比如我们在分析气象状况对交通的影响时，认为风力与降水量对交通的影响同等重要，但单从数值来看，风力的差值往往只有个位数，而不同时间段的降水量往往会相差两位数甚至三位数。如果未对数据处理的话，降水量这一维度对最终测得的距离影响较大。我们可以通过让数据归一化平衡数据对最终结果的影响程度。

当然了，加权的方式除了归一化，还有标准化等其他方法，归一化也会细分极值归一和均值归一，其他方法这里暂不展开。

#数据归一法
def norm(dataSet):
    #数据与标签分离
    numCol = dataSet.drop(dataSet.columns[-1],axis=1)
    lablesCol = dataSet.drop(dataSet.columns[:-1],axis=1)
    #极值归一
    minvals = numCol.min()
    maxvals = numCol.max()
    extremum = maxvals - minvals
    normDataSet = (numCol-minvals)/extremum
    normDataSet['lables'] = lablesCol
    return normDataSet

测试算法

这里的代码将数据集分成两部分，一部分用作训练，一部分用来测试，为了保证每次都是随机抽取，便将数据进行了打乱，让每一次测试的数据都不一样。

#iris数据集knn处理
def irisTest(k):
    practice = 0.2      #80%数据用作训练集，20%数据用作测试集
    iris = getIris()
    normIris = norm(iris)       					    #数据归一处理
    num = int(practice * normIris.shape[0])
    randomIris = np.random.permutation(normIris)        #将数据集顺序打乱
    forecastResult = classifier(randomIris[num:], randomIris[:num], k)
    wrongNum = 0
    
    #预测分类与实际分类对比，算出错误率
    for i in range(len(forecastResult)):
        print('预测分类：' + str(forecastResult[i]).ljust(20) + '实际分类：' + str(randomIris[i][-1]))
        if forecastResult[i] is not randomIris[i][-1]:
            wrongNum += 1
    print('错误个数：' + str(wrongNum) + '\t' + '错误率：' + str(wrongNum / num))

运行代码

现在可以跑一跑代码了，来看看结果（省略了部分预测结果）… … 算是实现基本功能了吧

if __name__ == '__main__':
    k = 5
    irisTest(k)

当然不会忘了，文章最开头的那个五角星是不是红色类呢，我们用sklearn库来看一下

# 续开头代码
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

clf = KNeighborsClassifier()
clf.fit(x, y)

x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, .02),
                     np.arange(y_min, y_max, .02))
z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
plt.scatter(x[:, 0],x[:, 1],c=y, cmap=plt.cm.spring, edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.plot(2.75, 3, 'b*',markersize=13)
plt.show()

利用分类器我们给数据分了区域，五角星的确是含在红类里面

matplotlib.cm文档：https://matplotlib.org/tutorials/colors/colormaps.html#classes-of-colormaps

参考：

• 《机器学习实战》
• 《深入浅出python机器学习》