MySQL --- 函数大全 7
目录
1.从地理哈希值返回纬度 ST_LatFromGeoHash()
2.点的返回纬度 ST_Latitude()
3.返回线字符串的长度 ST_Length()
4.从 WKT 构造线字符串 ST_LineFromText()/ ST_LineStringFromText()
5.从 WKB 构造线字符串 ST_LineFromWKB()/ ST_LineStringFromWKB()
6.沿线字符串的给定百分比点 ST_LineInterpolatePoint()
7.沿线字符串的给定百分比的点数 ST_LineInterpolatePoints()
8.从地理哈希值返回经度 ST_LongFromGeoHash()
9.返回点的经度 ST_Longitude()
10.围绕两点的矩形 ST_MakeEnvelope()
11.从 WKT 构造多线字符串 ST_MLineFromText() / ST_MultiLineStringFromText()
12.从 WKB 构造多线字符串 ST_MLineFromWKB()/ST_MultiLineStringFromWKB()
13.从 WKT 构建多点 ST_MPointFromText()/ ST_MultiPointFromText()\
14.从 WKB 构建多点 ST_MPointFromWKB()/ ST_MultiPointFromWKB()
15.从 WKT 构建多多边形 ST_MPolyFromText()/ ST_MultiPolygonFromText()
16.从 WKB 构建多多边形ST_MPolyFromWKB() / ST_MultiPolygonFromWKB()
17.返回几何集合中的几何数 ST_NumGeometries()
18.返回多边形中的内环数 ST_NumInteriorRing()/ ST_NumInteriorRings()
19.返回线字符串中的点数 ST_NumPoints()
20.一个几何图形是否与另一个几何图形重叠 ST_Overlaps()
21.沿线字符串的给定距离的点 ST_PointAtDistance()
22.将地理哈希值转换为点值 ST_PointFromGeoHash()
23.从 WKT 构造点 ST_PointFromText()
24.从 WKB 构造点 ST_PointFromWKB()
25.从 LineString 返回第 N 个点 ST_PointN()
26.从 WKT 构建多边形 ST_PolyFromText()/ ST_PolygonFromText()
27.从 WKB 构造多边形 ST_PolyFromWKB()/ ST_PolygonFromWKB()\
28.返回简化的几何图形 ST_Simplify()
29.返回几何的空间参考系统 ID ST_SRID()
30.线字符串的起点 ST_StartPoint()
31.交换了 X/Y 坐标的返回参数 ST_SwapXY()
32.返回点集两个几何形状的对称差值 ST_SymDifference()
33.一个几何图形是否与另一个几何图形接触 ST_Touches()
34.变换几何图形的坐标 ST_Transform()
35.两个几何图形的返回点集并集 ST_Union()
36.返回经过验证的几何图形 ST_Validate()
37.一个几何图形是否在另一个几何图形中 ST_Within()
38.返回点的 X 坐标 ST_X()
39.返回点的 Y 坐标 ST_Y()
40.计算语句摘要哈希值 STATEMENT_DIGEST()
41.计算规范化语句摘要 STATEMENT_DIGEST_TEXT()
42.返回总体标准差 STD()
43.返回总体标准差 STDDEV()
44.返回总体标准差 STDDEV_POP()
45.返回样本标准差 STDDEV_SAMP()
46.将字符串转换为日期 STR_TO_DATE()
47.比较两个字符串 STRCMP()
48.从日期中减去时间/日期间隔,然后返回日期 SUBDATE()
49.按指定返回子字符串 SUBSTR()
50.按指定返回子字符串 SUBSTRING()
1.从地理哈希值返回纬度 ST_LatFromGeoHash()
脚本
SELECT ST_LatFromGeoHash(ST_GeoHash(55,20,20));分析
从地理哈希字符串值返回纬度,作为 [−90, 90] 范围内的双精度数。
结果
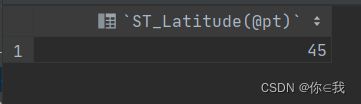
2.点的返回纬度 ST_Latitude()
脚本
SET @pt = ST_GeomFromText('POINT(45 80)', 4326);
分析
ST_Latitude(p [, new_latitude_val])
使用表示具有地理空间参考系统 (SRS) 的有效对象 p 的单个参数,ST_Latitude() 返回 纬度值 p 作为 双精度数字。Point
可选的第二个参数表示有效的 纬度值,ST_Latitude() 返回一个类似于第一个的对象 纬度等于第二个参数的参数。Point
结果
3.返回线字符串的长度 ST_Length()
脚本
SET @ls = ST_GeomFromText('LineString(1 1,2 2,3 3)'), @lss= ST_GeomFromText('MultiLineString((1 1,2 2,3 3),(4 4,5 5))');
select st_length(@ls),st_length(@lss);分析
ST_Length(ls [, unit])
返回一个双精度数字,指示长度 与其关联的空间中的 OR 值 ls 参考系统。值的长度等于总和 其元素的长度
结果
4.从 WKT 构造线字符串 ST_LineFromText()/ ST_LineStringFromText()
脚本
SELECT ST_LineFromText('LINESTRING(1 2, 3 4)');分析
ST_LineFromText 以 ST_LineString 类型的熟知文本表示和空间参考 ID 作为输入,并返回 ST_LineString 类型的对象。
结果
5.从 WKB 构造线字符串 ST_LineFromWKB()/ ST_LineStringFromWKB()
分析
ST_LineFromWKB(wkb [, srid [, options]]]), ST_LineStringFromWKB(wkb [, srid [, options]])
使用其 WKB 构造值 代表和 SRID
6.沿线字符串的给定百分比点 ST_LineInterpolatePoint()
脚本
SET @ls1 = ST_GeomFromText('LINESTRING(0 0,0 5,5 5)');
SELECT ST_AsText(ST_LineInterpolatePoint(@ls1, .5)),ST_AsText(ST_LineInterpolatePoint(@ls1, .75));分析
此函数采用几何图形 和 [0.0, 1.0] 范围内的分数距离并返回 沿着给定的分数 从起点到终点的距离。它可以使用 回答诸如几何学描述的道路中间的问题 论点。
结果
7.沿线字符串的给定百分比的点数 ST_LineInterpolatePoints()
脚本
SET @ls1 = ST_GeomFromText('LINESTRING(0 0,0 5,5 5)');
SELECT ST_AsText(ST_LineInterpolatePoints(@ls1, .5)),ST_AsText(ST_LineInterpolatePoints(@ls1, .75));分析
此函数采用几何图形 和范围 (0.0, 1.0) 中的分数距离并返回 由起点组成,加上沿距离每个部分的值 从起点到终点。它可以用来回答 诸如哪些值是谎言之类的问题 沿着几何形状描述的道路每 10% 的路程 论点
结果
8.从地理哈希值返回经度 ST_LongFromGeoHash()
脚本
SET @gh = ST_GeoHash(45,-20,10);
SELECT ST_AsText(ST_PointFromGeoHash(@gh,0));分析
ST_PointFromGeoHash(geohash_str, srid)
返回一个包含 解码的地理哈希值,给定一个地理哈希字符串值。
点的 X 和 Y 坐标是 范围 [−180, 180] 和范围内的纬度 [−90, 90],分别。
srid 参数是 32 位 无符号整数。
结果
9.返回点的经度 ST_Longitude()
脚本
SET @pt = ST_GeomFromText('POINT(45 90)', 4326);
SELECT ST_Latitude(@pt),ST_AsText(ST_Latitude(@pt,10));分析
ST_Latitude(p [, new_latitude_val])
使用表示具有地理空间参考系统 (SRS) 的有效对象 p 的单个参数,ST_Latitude() 返回 纬度值 p 作为 双精度数字
可选的第二个参数表示有效的 纬度值,ST_Latitude() 返回一个类似于第一个的对象 纬度等于第二个参数的参数
结果
10.围绕两点的矩形 ST_MakeEnvelope()
脚本
SET @pt1 = ST_GeomFromText('POINT(0 0)');
SET @pt2 = ST_GeomFromText('POINT(1 1)');
SELECT ST_AsText(ST_MakeEnvelope(@pt1, @pt2));分析
ST_MakeEnvelope(pt1, pt2)
返回在两个周围形成封套的矩形点
使用笛卡尔坐标系进行计算 而不是在球体、球体或地球上。
给定两个点 pt1 和 pt2,ST_MakeEnvelope() 创建 在抽象平面上的结果几何图形\
如果 pt1 和 pt2 相等,则结果为 点 pt1。
否则,如果是垂直或 水平线段,结果就是线段。(pt1, pt2)(pt1, pt2)
否则,结果是使用 pt1 和 pt2 作为对角线点的面。
结果
11.从 WKT 构造多线字符串 ST_MLineFromText() / ST_MultiLineStringFromText()
脚本
SELECT ST_AsText(ST_MLineFromText('MULTILINESTRING((1 2,3 4), (5 6,7 8))'));分析
语法
geometry ST_MLineFromText(text wKT , integer srid); geometry ST_MLineFromText(text wKT);参数
参数名称 描述 wKT WKT字符串。 srid Geometry对象的空间参考系ID。 描述
- 如果你很肯定输入的图形为MultiLine,使用ST_GeomFromTextST_GeomFromTextST_GeomFromText更快,因为没有多余的检测步骤。
- 如果未提供SRID,则默认为0。
- 如果WKT不是MultiLine,则返回null。
结果
12.从 WKB 构造多线字符串 ST_MLineFromWKB()/ST_MultiLineStringFromWKB()
分析
ST_MLineFromWKB 函数用于从 wkb 列中返回多线串。 sample_mlines 表具有一个几何列(用于存储多线串)和一个 wkb 列(用于存储多线串的 WKB 表示)。 SELECT 语句包含 ST_MLineFromWKB 函数,该函数用于从 wkb 列检索多线串。
13.从 WKT 构建多点 ST_MPointFromText()/ ST_MultiPointFromText()\
脚本
SELECT ST_AsText(ST_MPointFromText('MULTIPOINT(1 2,3 4)'));分析
语法
geometry ST_MPointFromText(text wKT , integer srid); geometry ST_MPointFromText(text wKT);参数
参数名称 描述 wKT WKT字符串。 srid Geometry对象的空间参考系ID。 描述
- 如果你很肯定输入的图形为MultiPoint,使用ST_GeomFromTextST_MPointFromText()ST_GeomFromText更快,因为没有多余的检测步骤。
- 如果未提供SRID,则默认为0。
- 如果WKT不是MultiPoint,则返回null。
结果
14.从 WKB 构建多点 ST_MPointFromWKB()/ ST_MultiPointFromWKB()
分析
ST_MPointFromWKB 从熟知二进制表示创建多线串。几何是空间参考系统 4326 中的多点。在本示例中,多点存储在 SAMPLE_MPOINTS 表的几何列中且 ID = 10,然后利用熟知二进制表示对 WKB 列进行更新(使用 ST_AsBinary 函数)。最后,ST_MPointFromWKB 函数用于从 WKB 列中返回多点。SAMPLE_MPOINTS 表具有一个 GEOMETRY 列(用于存储多点)和一个 WKB 列(用于存储多点的熟知二进制表示)。
15.从 WKT 构建多多边形 ST_MPolyFromText()/ ST_MultiPolygonFromText()
脚本
SELECT ST_AsText(ST_MPolyFromText('MULTIPOLYGON(((0 0,1 0,1 1,0 0),(1 1,2 1,2 2,1 1)))'));分析
语法
geometry ST_MPolyFromText(text wKT , integer srid); geometry ST_MPolyFromText(text wKT);参数
参数名称 描述 wKT WKT字符串。 srid Geometry对象的空间参考系ID。 描述
- 如果你很肯定输入的图形为MultiPolygon,使用ST_GeomFromTextST_MPolyFromText()ST_GeomFromText更快,因为没有多余的检测步骤。
- 如果未提供SRID,则默认为0。
- 如果WKT不是MultiPolygon,则返回NULL。
结果
16.从 WKB 构建多多边形ST_MPolyFromWKB() / ST_MultiPolygonFromWKB()
分析
ST_MPolyFromWKB 由熟知二进制表示创建多面对象。几何是空间参考系统 4326 中的多面。在本示例中,多面存储在 sample_mpolys 表的几何列中且 ID = 10,然后利用熟知二进制表示对 wkb 列进行更新(使用 ST_AsBinary 函数)。最后,ST_MPolyFromWKB 函数用于从 wkb 列中返回多面。sample_mpolys 表格具有一个几何列(用于存储多面)和一个 wkb 列(用于存储多面的 WKB 表示)。
17.返回几何集合中的几何数 ST_NumGeometries()
脚本
SET @gc = 'GeometryCollection(Point(1 1),LineString(2 2, 3 3))';
SELECT ST_NumGeometries(ST_GeomFromText(@gc));分析
ST_NumGeometries(gc)
返回值 gc 中的几何数
结果
18.返回多边形中的内环数 ST_NumInteriorRing()/ ST_NumInteriorRings()
脚本
SET @poly = 'Polygon((0 0,0 3,3 3,3 0,0 0),(1 1,1 2,2 2,2 1,1 1))';
SELECT ST_NumInteriorRings(ST_GeomFromText(@poly));
结果
19.返回线字符串中的点数 ST_NumPoints()
脚本
SET @ls = 'LineString(1 1,2 2,3 3)';
SELECT ST_NumPoints(ST_GeomFromText(@ls));结果
20.一个几何图形是否与另一个几何图形重叠 ST_Overlaps()
脚本
SET @ls1 = ST_GeomFromText('LINESTRING(0 0,-0.00 0,0.0 0)');
SET @ls2 = ST_GeomFromText('LINESTRING(0 0, 1 1)');
SELECT ST_Overlaps(@ls1, @ls2);分析
ST_Overlaps(g1, g2)
两个几何在空间上重叠,如果 它们相交,它们的相交产生几何图形 具有相同的维度,但不等于给定的任何一个 几何。
此函数返回 1 或 0 以指示 g1 在空间上是否与 g2 重叠。
结果
21.沿线字符串的给定距离的点 ST_PointAtDistance()
分析
此函数采用几何图形 和 [0.0,ST_Length(ls)] 范围内的距离 以空间参考系统 (SRS) 的单位测量 ,并返回从其起点开始的沿该距离 点。它可用于回答诸如哪个值是从 400 米开始的问题 几何参数描述的道路。
22.将地理哈希值转换为点值 ST_PointFromGeoHash()
脚本
SET @gh = ST_GeoHash(45,-20,10);
SELECT ST_AsText(ST_PointFromGeoHash(@gh,0));分析
返回一个包含 解码的地理哈希值,给定一个地理哈希字符串值。
点的 X 和 Y 坐标是 范围 [−180, 180] 和范围内的纬度 [−90, 90]
结果
23.从 WKT 构造点 ST_PointFromText()
分析
语法
geometry ST_PointFromText(text wKT); geometry ST_PointFromText(text wKT , integer srid);参数
参数名称 描述 wKT WKT字符串。 srid Geometry对象的空间参考系ID。 描述
- 如果未提供SRID,则默认为0。
- 如果WKT不是Point,则返回NULL。
- 如果WKT完全无效,则抛出错误。
- 如果你很肯定输入的图形为Point,使ST_GeomFromText更快,因为没有多余的检测步骤。
- 如果要从经纬度坐标构建点,并且比OGC兼容更在意性能和准确性,请使ST_MakePoint和ST_Point函数。
24.从 WKB 构造点 ST_PointFromWKB()
分析
语法
geometry ST_GeomFromWKB(bytea geom); geometry ST_GeomFromWKB(bytea geom , integer srid);参数
参数名称 描述 geom WKB串。 srid Geometry对象的坐标系ID。 描述
- 如果未指定SRID,则默认值为0。
- 如果输入的WKB串不表示Point对象,则返回NULL。
- 该函数支持3D对象,并且不会丢弃Geometry对象的z-index。
- 该函数支持Circular Strings和Curves。
25.从 LineString 返回第 N 个点 ST_PointN()
脚本
SET @ls = 'LineString(1 1,2 2,3 3)';
SELECT ST_AsText(ST_PointN(ST_GeomFromText(@ls),2));26.从 WKT 构建多边形 ST_PolyFromText()/ ST_PolygonFromText()
分析
语法
geometry ST_PolygonFromText(text wKT); geometry ST_PolygonFromText(text wKT , integer srid);参数
参数名称 描述 wKT WKT字符串。 srid Geometry对象的空间参考系ID。 描述
- 如果未指定SRID,则默认值为0。
- 如果输入的WKT串不能表示Polygon对象,则返回NULL。
- 如果输入的WKT确定可以表示polygon对象,则使ST_GeomFromText更快,因为没有多余的检测步骤。
27.从 WKB 构造多边形 ST_PolyFromWKB()/ ST_PolygonFromWKB()\
分析
ST_PolyFromWKB 从熟知二进制表示创建面。几何是空间参考系统 4326 中的面。在本示例中,面存储在 sample_polys 表的几何列中且 ID = 1115,然后利用 WKB 表示对 wkb 列进行更新(使用 ST_AsBinary 函数)。最后,ST_PolyFromWKB 函数用于从 WKB 列中返回多面。sample_polys 表具有一个几何列(用于存储面)和一个 wkb 列(用于存储面的 WKB 表示)。
28.返回简化的几何图形 ST_Simplify()
脚本
SET @g = ST_GeomFromText('LINESTRING(0 0,0 1,1 1,1 2,2 2,2 3,3 3)');
SELECT ST_AsText(ST_Simplify(@g, 0.5)),ST_AsText(ST_Simplify(@g, 1.0));
分析
用道格拉斯-皮克算法简化几何图形,并且 返回相同类型的简化值。
几何可以是任何几何类型,尽管 Douglas-Peucker算法实际上可能不会处理每种类型。 几何集合通过为其组件提供来处理 一个接一个地简化算法,并返回 因此,几何图形被放入几何集合中。
max_distance参数是 顶点到的距离(以输入坐标为单位) 要删除的其他段。此距离内的顶点 简化的线串将被删除。
29.返回几何的空间参考系统 ID ST_SRID()
脚本
SET @g = ST_GeomFromText('LineString(1 1,2 2)', 0),@g1 = ST_GeomFromText('LineString(1 1,2 2)', 4326);
SELECT ST_SRID(@g), ST_SRID(@g1);分析
ST_SRID(g [, srid])
使用表示有效几何对象 g 的单个参数,ST_SRID() 返回一个整数 指示空间参考系统 (SRS) 的 ID 与 G 相关。
可选的第二个参数表示有效的 SRID 值, ST_SRID() 返回一个 与具有 SRID 的第一个参数类型相同的对象 值等于第二个参数。这仅设置 SRID 对象的值;它不执行任何转换 的坐标值。
结果
30.线字符串的起点 ST_StartPoint()
脚本
SET @ls = 'LineString(1 1,2 2,3 3)';
SELECT ST_AsText(ST_StartPoint(ST_GeomFromText(@ls)));结果
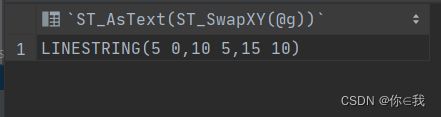
31.交换了 X/Y 坐标的返回参数 ST_SwapXY()
脚本
SET @g = ST_LineFromText('LINESTRING(0 5,5 10,10 15)');
SELECT ST_AsText(ST_SwapXY(@g));分析
接受内部几何格式的参数,交换 X 和几何图形中每个坐标对的 Y 值,以及 返回结果。
结果
32.返回点集两个几何形状的对称差值 ST_SymDifference()
脚本
SET @g1 = ST_GeomFromText('MULTIPOINT(5 0,15 10,15 25)');
SET @g2 = ST_GeomFromText('MULTIPOINT(1 1,15 10,15 25)');
SELECT ST_AsText(ST_SymDifference(@g1, @g2));分析
返回表示对称点集的几何图形 几何值
g1和g2的差异,定义为:g1 symdifference g2 := (g1 union g2) difference (g1 intersection g2)或者,在函数调用表示法中:
ST_SymDifference(g1, g2) = ST_Difference(ST_Union(g1, g2), ST_Intersection(g1, g2))
结果
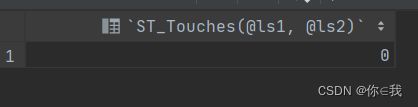
33.一个几何图形是否与另一个几何图形接触 ST_Touches()
脚本
SET @ls1 = ST_GeomFromText('LINESTRING(0 0,-0.00 0,0.0 0)');
SET @ls2 = ST_GeomFromText('LINESTRING(0 0, 1 1)');
SELECT ST_Touches(@ls1, @ls2);分析
两个几何形状在空间上接触,如果它们的 内部不相交,但其中一个的边界 几何图形与 的边界或内部相交 另一个。
结果
34.变换几何图形的坐标 ST_Transform()
脚本
SET @p = ST_GeomFromText('POINT(52.381389 13.064444)', 4326);
SET @p = ST_Transform(@p, 4230);
SELECT ST_AsText(@p);分析
从一个空间参考系统 (SRS) 变换几何 到另一个。返回值是与 所有坐标都转换为 目标 SRID,
target_srid。 转换支持仅限于地理 SRS,除非 几何参数的 SRID 与目标相同 SRID 值,在这种情况下,返回值是输入 任何有效 SRS 的几何图形。
结果
35.两个几何图形的返回点集并集 ST_Union()
脚本
SET @g1 = ST_GeomFromText('LineString(1 1, 3 3)');
SET @g2 = ST_GeomFromText('LineString(1 3, 3 1)');
SELECT ST_AsText(ST_Union(@g1, @g2));分析
返回一个几何图形,该几何图形表示 几何值
g1和g2。结果在相同的 SRS 中 作为几何参数。
结果
36.返回经过验证的几何图形 ST_Validate()
脚本
SET @ls1 = ST_GeomFromText('LINESTRING(0 0)');
SET @ls2 = ST_GeomFromText('LINESTRING(0 0, 1 1)');
SELECT ST_AsText(ST_Validate(@ls1)),ST_AsText(ST_Validate(@ls2));分析
根据 OGC 规范验证几何图形。一个 几何图形的语法格式可以很好(WKB 值加上 SRID),但在几何上无效。例如,此多边形是 几何上无效:POLYGON((0 0, 0 0, 0 0, 0 0, 0 0))
ST_Validate() 返回 几何图形,如果它在语法上格式良好并且 几何上有效,如果参数 语法格式不正确或几何上无效 或者是 。
ST_Validate() 可用于 过滤掉无效的几何数据,尽管需要付出代价。为 需要更精确结果且不受污染的应用 无效数据,这种惩罚可能是值得的。
如果几何参数有效,则按原样返回, 除了如果输入或有顺时针响铃,那些 在检查有效性之前,环被反转。如果 几何形状有效,反转环的值为 返回。
唯一有效的空几何图形以 空几何集合值。ST_Validate() 返回它 在这种情况下,无需进一步检查即可直接进行。
结果
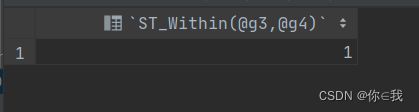
37.一个几何图形是否在另一个几何图形中 ST_Within()
脚本
SET @g3 = ST_GeomFromText('Polygon((0 0,0 3,3 3,3 0,0 0))');
SET @g4 = ST_GeomFromText('Polygon((0 0,0 3,3 3,3 0,0 0))');
SELECT ST_Within(@g3,@g4);分析
返回 1 或 0 以指示
g1在空间上是否在g2内。这测试相反 关系作为ST_Contains
结果
38.返回点的 X 坐标 ST_X()
脚本
SELECT ST_X(Point(56.7, 53.34));结果
39.返回点的 Y 坐标 ST_Y()
脚本
SELECT ST_Y(Point(56.7, 53.34));结果
40.计算语句摘要哈希值 STATEMENT_DIGEST()
脚本
SET @stmt = 'SELECT * FROM mytable WHERE cola = 10 AND colb = 20';
SELECT STATEMENT_DIGEST(@stmt);分析
给定一个字符串形式的 SQL 语句,返回该语句 将哈希值摘要为连接字符集中的字符串
结果
41.计算规范化语句摘要 STATEMENT_DIGEST_TEXT()
脚本
SET @stmt = 'SELECT * FROM mytable WHERE cola = 10 AND colb = 20';
SELECT STATEMENT_DIGEST_TEXT(@stmt);分析
给定一个字符串形式的 SQL 语句,返回规范化的 语句摘要为连接字符集中的字符串
结果
42.返回总体标准差 STD()
脚本
create table a
(
id int auto_increment primary key,
score int
);
insert into a (score)
values (90),
(90),
(85),
(80),
(70);
insert into a (score) value (100);
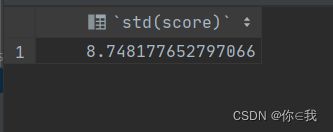
select std(score) from a;
分析
总体标准差是总体各单位标志值与算术平均数之间的平均离差,用σ表示。
总体方差是一组资料中各数值与其算术平均数离差平方和的平均数。总体标准差则是总体方差的平方根。
标准差是最常用和最重要的变异性测量。标准差以分布的平均数作为参照点,用考虑每个数据和平均 数之间的距离来测量变异性。它由数据是否接近或远离平均数来决定。也就是说,它考虑数据是聚集还是离散的?简单来说,标准差与数据到平均数的平均距离近似。
结果
43.返回总体标准差 STDDEV()
脚本
create table a
(
id int auto_increment primary key,
score int
);
insert into a (score)
values (90),
(90),
(85),
(80),
(70);
insert into a (score) value (100);
select stddev(score) from a;分析
和上一个一样
结果
44.返回总体标准差 STDDEV_POP()
脚本
create table a
(
id int auto_increment primary key,
score int
);
insert into a (score)
values (90),
(90),
(85),
(80),
(70);
insert into a (score) value (100);
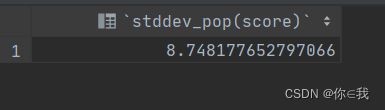
select stddev_pop(score) from a;
分析
和上一个一样
结果
45.返回样本标准差 STDDEV_SAMP()
脚本
create table a
(
id int auto_increment primary key,
score int
);
insert into a (score)
values (90),
(90),
(85),
(80),
(70);
insert into a (score) value (100);
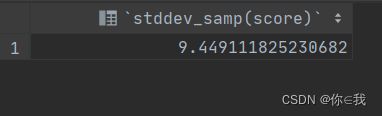
select stddev_samp(score) from a;
分析
样本标准差是总体标准差的点估计,当调查量非常大或者生产线一直生产某类产品,无法估计总体平均值和总体标准差时,才用样本的点估计,估计总体参数。
结果
46.将字符串转换为日期 STR_TO_DATE()
脚本
SELECT STR_TO_DATE('16,12,2022','%d,%m,%Y');分析
语法
STR_TO_DATE(string, format)
参数值
参数 描述 string 必需。要格式化为日期的字符串 format 必需。要使用的格式。 可以是以下值之一或组合:
格式 描述 %a 工作日的缩写名称(周日至周六) %b 缩写月份名称(1 月至 12 月) %c 数字月份名称(0 到 12) %D 以数字形式表示的月份中的日期,后跟后缀 (1st, 2nd, 3rd, ...) %d 以数值表示的月份中的日期(01 到 31) %e 以数字形式表示的月份中的日期(0 到 31) %f 微秒(000000 到 999999) %H 小时(00 到 23) %h 小时(00 到 12) %I 小时(00 到 12) %i 分钟(00 到 59) %j 一年中的某一天(001 到 366) %k 小时(0 到 23) %l 小时(1 到 12) %M 完整的月份名称(1 月至 12 月) %m 数字形式的月份名称(01 到 12) %p 上午或下午 %r 12 小时 AM 或 PM 格式的时间 (hh:mm:ss AM/PM) %S 秒(00 到 59) %s 秒(00 到 59) %T 24 小时制时间 (hh:mm:ss) %U 星期天是一周的第一天(00 到 53) %u 星期一是一周的第一天的星期(00 到 53) %V 星期天是一周的第一天(01 到 53)。与 %X 一起使用 %v 星期一是一周的第一天的星期(01 到 53)。与 %X 一起使用 %W 完整的工作日名称(周日至周六) %w 星期天=0,星期六=6 %X 星期天是一周的第一天的星期。与 %V 一起使用 %x 星期一是一周的第一天的一周的年份。与 %V 一起使用 %Y 4 位数字形式的年份 %y 2 位数字形式的年份
结果
47.比较两个字符串 STRCMP()
脚本
select strcmp('li','li'),strcmp('li','il');分析
STRCMP (str1, str2) 比较两个字符串,如果这两个字符串相等返回0,如果第一个参数是根据当前的排序小于第二个参数顺序返回-1,否则返回1。
结果
48.从日期中减去时间/日期间隔,然后返回日期 SUBDATE()
脚本
SELECT SUBDATE('2022-12-16', INTERVAL 15 MINUTE),SUBDATE(NOW(),INTERVAL 1 WEEK );分析
语法
SUBDATE(date, INTERVAL value unit)
OR:
SUBDATE(date, days)
参数值
参数 描述 date 必需。原日期 days 必需。从 date 中减去的天数 value 必需。要减去的时间/日期间隔的值。 正负值都可以 unit 必需。区间的类型。 可以是以下值之一:
- MICROSECOND
- SECOND
- MINUTE
- HOUR
- DAY
- WEEK
- MONTH
- QUARTER
- YEAR
- SECOND_MICROSECOND
- MINUTE_MICROSECOND
- MINUTE_SECOND
- HOUR_MICROSECOND
- HOUR_SECOND
- HOUR_MINUTE
- DAY_MICROSECOND
- DAY_SECOND
- DAY_MINUTE
- DAY_HOUR
- YEAR_MONTH
结果
49.按指定返回子字符串 SUBSTR()
脚本
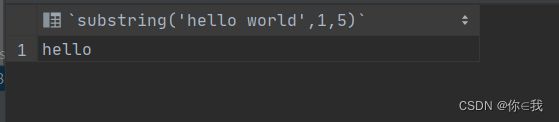
select substr('hello world',1,5)分析
语法
SUBSTR(string, start, length)
OR:
SUBSTR(string FROM start FOR length)
参数值
参数 描述 string 必需。要从中提取的字符串 start 必需。起始位置。 可以是正数或负数。 如果是正数,则此函数从字符串的开头提取。 如果是负数,此函数从字符串的末尾提取 length 可选。要提取的字符数。 如果省略,将返回整个字符串(从 start 位置开始)
结果
50.按指定返回子字符串 SUBSTRING()
脚本
select substring('hello world',1,5);分析
与substr一样
结果
函数大全1
函数大全2
函数大全3
函数大全4
函数大全5
函数大全6