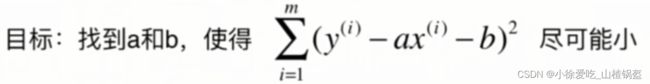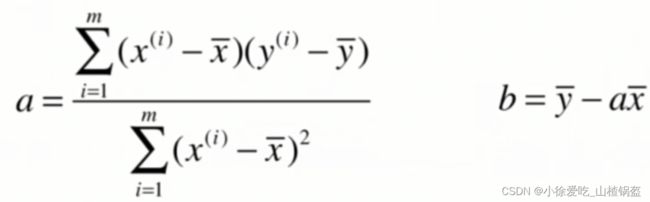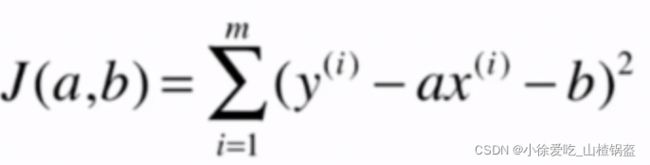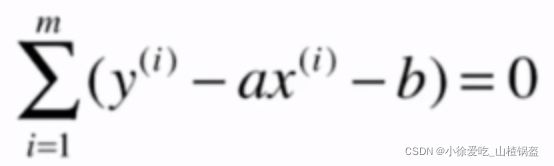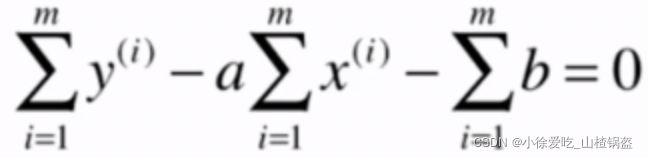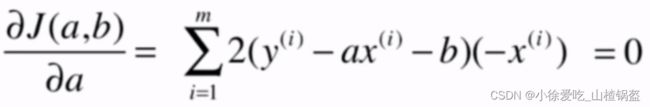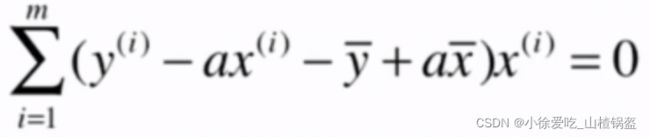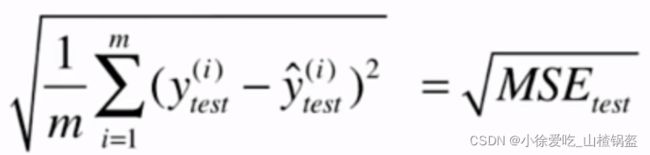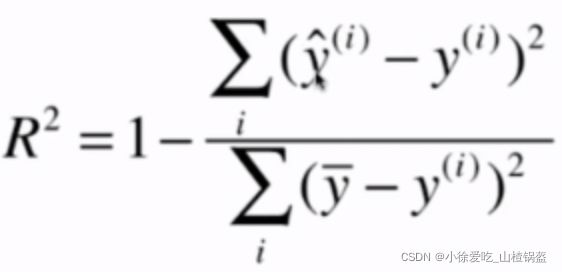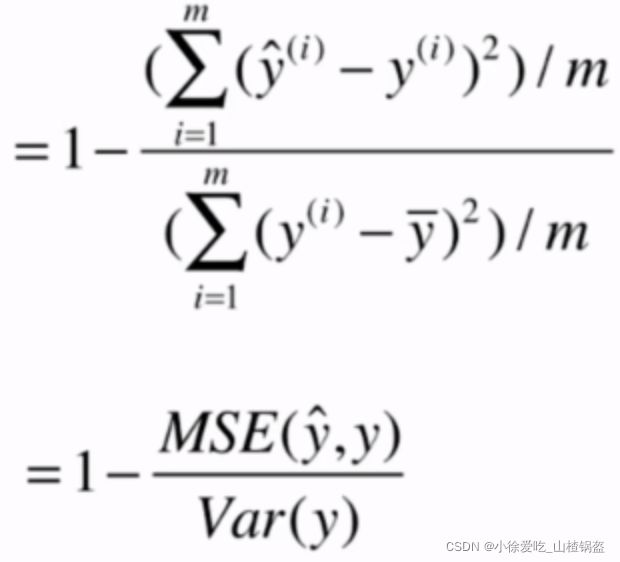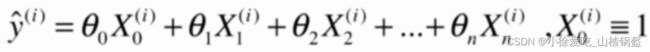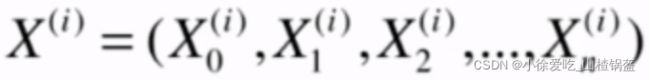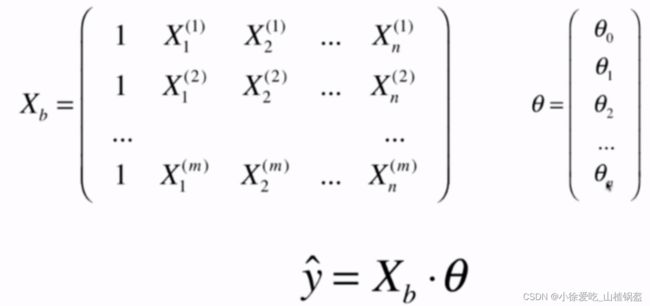02机器学习--简单线性回归及python实现
目录
①概述
②最小二乘法
③实现简单线性回归(Simple Linear Regression)
④评测标准
⑤多元线性回归
⑥scikit-learn中使用线性回归法
⑦扩展(kNN回归)
⑧总结
①概述
机器学习的思路:找到一个模型(在线性回归中就是直线的参数)最大程度的拟合我们的数据,在线性回归中,这个模型就是一条直线,本质上是优化损失函数,获得机器学习。(可以说几乎所有的参数学习的算法都是这样一个套路),对于简单线性回归:(y是真值,ax+b是预测值)
②最小二乘法
这是典型的最小二乘法问题:最小化误差的平方,最终可以计算出a,b
最小二乘法数学推导:
损失函数:
对b求偏导:
化简:
对a求偏导:
带入b:
进一步优化a的表达式:
③实现简单线性回归(Simple Linear Regression)
1.for循环实现(效率较低)
# 用自己编的数据简单实现一下
import numpy as np
import matplotlib.pyplot as plt
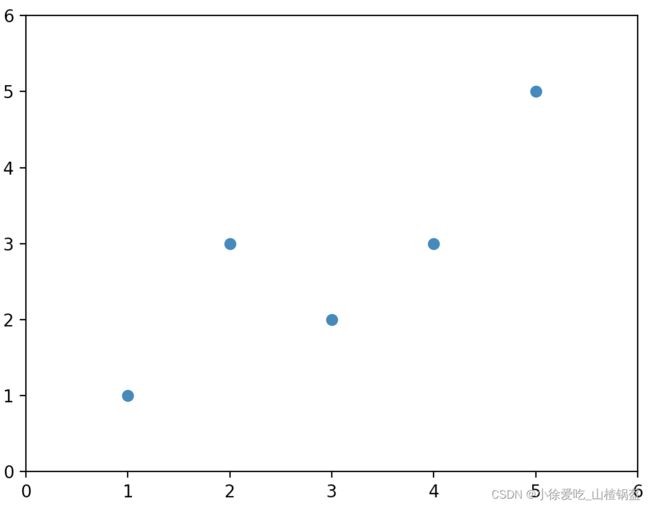
x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 3, 2, 3, 5])
# plt.scatter(x, y)
# plt.axis([0, 6, 0, 6])
# plt.show() # 画一下散点图
# 实现上面推导的最小二乘法
x_mean = np.mean(x)
y_mean = np.mean(y) # 求均值
num = 0.0 # 分子
d = 0.0 # 分母
for x_i, y_i in zip(x, y): # 每次相应的从x和y中取一个值
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
# 求出a和b
a = num/d
b = y_mean - a * x_mean
y_hat = a * x + b
# 画一下回归直线
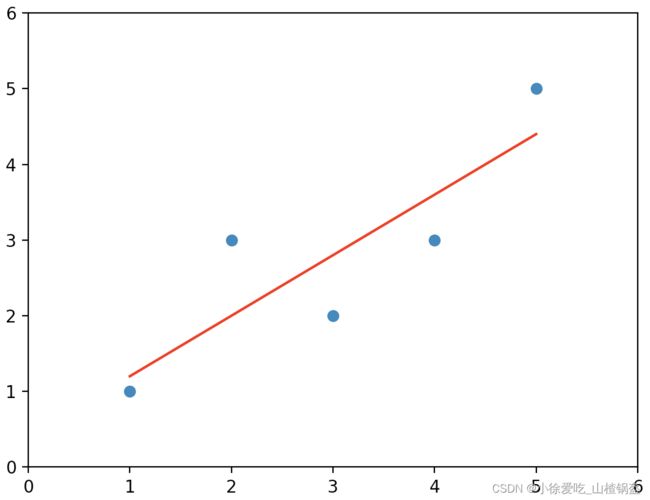
# plt.scatter(x, y) # 原始数据
# plt.plot(x, y_hat, color='r') # 预测数据
# plt.axis([0, 6, 0, 6]) # 坐标轴范围
# plt.show()
# 做一下预测
x_predict = 6
y_predict = a * x_predict + b
print(y_predict)输出结果:
原始数据散点图:
预测回归后的直线和原始数据图:
预测的结果:
2.向量化运算(效率较高)
不难发现a的分子和分母都是这样一种形式:(向量的点乘)
# 原来for循环求a
x_mean = np.mean(x_train)
y_mean = np.mean(y_train) # 求均值
num = 0.0 # 分子
d = 0.0 # 分母
for x_i, y_i in zip(x_train, y_train): # 每次相应的从x和y中取一个值
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
# 优化后使用向量的点乘
x_mean = np.mean(x_train)
y_mean = np.mean(y_train) # 求均值
num = 0.0 # 分子
d = 0.0 # 分母
num = (x_train - x_mean).dot(y_train - y_mean)
d = (x_train - x_mean).dot(x_train - x_mean)
④评测标准
评测标准
疑问:这个标准和m相关 ?
1.改进一下衡量标准:均方误差(Mean Squared Error)MSE
疑问:量纲?y的单位如果是万元,MSE算出来是万元的平方
2.改进一下:均方根误差(Root Mean Squared Error)RMSE
3.平均绝对误差(Mean Absolute Error) MAE
MSE&&MAE
# scikit-learn中的MSE和MAE的调用方法
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
mean_squared_error(y_test, y_predict)
mean_absolute_error(y_test, y_predict)疑问:上述方法针对不同问题得到的结果,无法进行直接比较。(RMSE和MAE局限性)
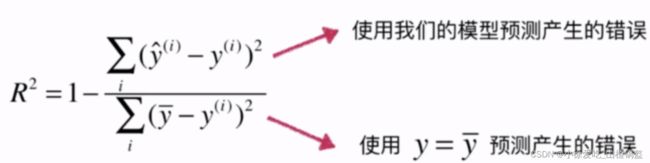
4. R Squared(R^2)
理解:
最后相当于衡量了我们的模型拟合成功的部分的效果
from sklearn.metrics import r2_score
r2_score(y_test, y_predict)⑤多元线性回归
这里不展示推导过程(和一元线性回归相似),正规方程解:
问题:时间复杂度比较高
# 训练过程
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # x_train前面加了一列1
theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0] # 截距theta0
self.coef_ = self._theta[1:] # 系数⑥scikit-learn中使用线性回归法
# 用房价数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0] # 去除可能异常的值
y = y[y < 50.0]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
print(lin_reg.coef_) # 系数矩阵
print(lin_reg.intercept_) # 截距
print(lin_reg.score(X_test, y_test)) # R^2输出结果:
⑦扩展(kNN回归)
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
# 划分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)
# 数据归一化
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
# 直接调用kNN回归,搜索超参数
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
print(knn_reg.score(X_test_standard, y_test))
# 利用网格搜索得到最佳回归算法
from sklearn.model_selection import GridSearchCV
param_grid = [
{
"weights": ["uniform"],
"n_neighbors": [i for i in range(1, 11)]
},
{
"weights": ["distance"],
"n_neighbors": [i for i in range(1, 11)],
"p": [i for i in range(1,6)]
}
]
knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)
grid_search.fit(X_train_standard, y_train)
#输出
print(grid_search.best_params_)
print(grid_search.best_score_) # 这个结果使用的验证方式和knn_reg.score的验证方式不一样,因为网格搜索使用了交叉验证
print(grid_search.best_estimator_.score(X_test_standard, y_test)) # 最佳模型得分输出结果:
网格搜索参考:Scikit中使用Grid_Search来获取模型的最佳参数_npupengsir的博客-CSDN博客_best_estimator_
⑧总结
典型的参数学习
只能解决回归问题
对数据有假设