算法导论 第二十四章 单源最短路径
def:单源最短路径既从节点s出发到其他的所有能到达的节点的的最短路径。
对于存在权重为负数的边,只要这边不形成环,或者整个环路的权重大于零则可以认为最短路径依然有解。
我们使用前驱子图来表现最短路径
我们使用如下代码来表示图与最短路径:
class Vertex:
def __init__(self, u):
self.value = u
self.vertexs = []
self.isInGraph = False
self.pi = None
self.d = float("inf")
class Edge:
def __init__(self, u, v, w):
self.fromV = u
self.toV = v
self.weight = w
class Graph:
def __init__(self):
self.vertexs = []
self.edges = []
def weight(edges, u, v):
for e in edges:
if e.fromV == u and e.toV == v:
return e.weight
return None
def INITGRAPH(G, edges):
for e in edges:
if not e.fromV.isInGraph:
G.vertexs.append(e.fromV)
e.fromV.isInGraph = True
if not e.toV.isInGraph:
G.vertexs.append(e.toV)
e.toV.isInGraph = True
G.edges.append(e)
e.fromV.vertexs.append(e.toV)
#e.toV.vertexs.append(e.fromV)
def INITIALIZE_SINGLE_SOURCE(G, s):
for v in G.vertexs:
v.d = float("inf")
s.d = 0
def RELAX(u, v, edges):
if v.d > u.d + weight(edges, u, v):
v.d = u.d + weight(edges, u, v)
v.pi = u
print(u.value, v.value, v.d)
24.1 BELLMAN_FORD算法
def BELLMAN_FORD(G, s):
INITIALIZE_SINGLE_SOURCE(G, s)
for i in range(1, len(G.vertexs)-1):
for edge in G.edges:
RELAX(edge.fromV, edge.toV, G.edges)
for edge in G.edges:
if edge.toV.d > edge.fromV.d + weight(edges, edge.fromV, edge.toV):
return False
return True
if __name__ == "__main__":
s = Vertex('s')
t = Vertex('t')
x = Vertex('x')
y = Vertex('y')
z = Vertex('z')
edges = []
edges.append(Edge(x, t, -2))
edges.append(Edge(t, x, 5))
edges.append(Edge(t, y, 8))
edges.append(Edge(t, z, -4))
edges.append(Edge(y, x, -3))
edges.append(Edge(y, z, 9))
edges.append(Edge(z, x, 7))
edges.append(Edge(z, s, 2))
edges.append(Edge(s, t, 6))
edges.append(Edge(s, y, 7))
G = Graph()
INITGRAPH(G, edges)
BELLMAN_FORD(G, s)

24.2 有向无环图中的单源最短路径问题
对于无环图而言,先进行拓扑排序在对每条边进行一次松弛,就可得到正确的结果。
WHITE, GRAY, BLACK = (0, 1, 2)
class Vertex:
def __init__(self, u):
self.value = u
self.vertexs = []
self.isInGraph = False
self.pi = None
self.d = float("inf")
self.color = WHITE
class Edge:
def __init__(self, u, v, w):
self.fromV = u
self.toV = v
self.weight = w
class Graph:
def __init__(self):
self.vertexs = []
self.edges = []
def weight(edges, u, v):
for e in edges:
if e.fromV == u and e.toV == v:
return e.weight
return None
def INITGRAPH(G, edges):
for e in edges:
if not e.fromV.isInGraph:
G.vertexs.append(e.fromV)
e.fromV.isInGraph = True
if not e.toV.isInGraph:
G.vertexs.append(e.toV)
e.toV.isInGraph = True
G.edges.append(e)
e.fromV.vertexs.append(e.toV)
def DFS(G, TG):
for u in G.vertexs:
u.color = WHITE
u.pi = None
for u in G.vertexs:
if u.color == WHITE:
DFS_VISIT(G, u, TG)
def DFS_VISIT(G, u, TG):
u.color = GRAY
for v in u.vertexs:
if v.color == WHITE:
v.pi = u
DFS_VISIT(G, v, TG)
u.color = BLACK
TG.append(u)
def TOPOLOGICAL_SORT(G):
TSG = []
DFS(G, TSG)
return TSG
def PRINT_TSG(tsg):
for u in tsg:
print(u.value)
def INITIALIZE_SINGLE_SOURCE(G, s):
for v in G.vertexs:
v.d = float("inf")
s.d = 0
def RELAX(u, v, edges):
if v.d > u.d + weight(edges, u, v):
v.d = u.d + weight(edges, u, v)
v.pi = u
print("relax", u.value, v.value, v.d)
def DAG_SHORTEST_PATHS(G, s):
tsg = TOPOLOGICAL_SORT(G)
INITIALIZE_SINGLE_SOURCE(G, s)
#PRINT_TSG(tsg)
for u in tsg[::-1]:
for v in u.vertexs:
RELAX(u, v, G.edges)
print(u.value, u.d)
if __name__ == "__main__":
r = Vertex('r')
s = Vertex('s')
t = Vertex('t')
x = Vertex('x')
y = Vertex('y')
z = Vertex('z')
edges = []
edges.append(Edge(t, z, 2))
edges.append(Edge(t, x, 7))
edges.append(Edge(r, s, 5))
edges.append(Edge(r, t, 3))
edges.append(Edge(x, y, -1))
edges.append(Edge(s, t, 2))
edges.append(Edge(s, x, 6))
edges.append(Edge(t, y, 4))
edges.append(Edge(x, z, 1))
edges.append(Edge(y, z, -2))
G = Graph()
INITGRAPH(G, edges)
DAG_SHORTEST_PATHS(G, s)
def PARENT(i):
return (i-1) // 2
def LEFT(i):
return i*2 + 1
def RIGHT(i):
return i*2 + 2
def MIN_HEAPIFY(A, i, size):
l = LEFT(i)
r = RIGHT(i)
if l < size and A[l] < A[i]:
largest = l
else:
largest = i
if r < size and A[r] < A[largest]:
largest = r
if largest != i:
temp = A[i]
A[i] = A[largest]
A[largest] = temp
MIN_HEAPIFY(A, largest, size)
def BUILD_MIN_HEAP(A):
size = len(A)
for i in range(len(A)//2, -1, -1):
MIN_HEAPIFY(A, i, size)
def HEAP_MINIMUM(A):
return A[0]
def HEAP_EXTRACT_MIN(A, size):
assert(size > 0)
iMIN = A[0]
size = size - 1
A[0] = A[size]
MIN_HEAPIFY(A, 0, size)
return iMIN
def HEAP_DECREASE_KEY(A, i, key):
assert(A[i] == key)
A[i] = key
while i > 0 and PARENT(i) >= 0 and A[PARENT(i)] > A[i]:
temp = A[i]
A[i] = A[PARENT(i)]
A[PARENT(i)] = temp
i = PARENT(i)
def MIN_HEAP_INSERT(A, key):
A.append(float("inf"))
HEAP_DECREASE_KEY(A, len(A)-1, key)
#模拟获取index的功能,假设为常数时间
def HEAP_INDEX(A, size, x):
for i in range(0, size):
if A[i] == x:
return i
#======================================================
WHITE, GRAY, BLACK = (0, 1, 2)
class Vertex:
def __init__(self, u):
self.value = u
self.vertexs = []
self.isInGraph = False
self.pi = None
self.d = float("inf")
self.color = WHITE
def __lt__(self, u):
return self.d < u.d
class Edge:
def __init__(self, u, v, w):
self.fromV = u
self.toV = v
self.weight = w
class Graph:
def __init__(self):
self.vertexs = []
self.edges = []
def weight(edges, u, v):
for e in edges:
if e.fromV == u and e.toV == v:
return e.weight
return None
def INITGRAPH(G, edges):
for e in edges:
if not e.fromV.isInGraph:
G.vertexs.append(e.fromV)
e.fromV.isInGraph = True
if not e.toV.isInGraph:
G.vertexs.append(e.toV)
e.toV.isInGraph = True
G.edges.append(e)
e.fromV.vertexs.append(e.toV)
def INITIALIZE_SINGLE_SOURCE(G, s):
for v in G.vertexs:
v.d = float("inf")
s.d = 0
def RELAX(Q, size, u, v, edges):
if v.d > u.d + weight(edges, u, v):
index = HEAP_INDEX(Q, size, v)
v.d = u.d + weight(edges, u, v)
HEAP_DECREASE_KEY(Q, index, v)
v.pi = u
print("relax", u.value, v.value, v.d)
def DIJKSTRA(G, s):
INITIALIZE_SINGLE_SOURCE(G, s)
S = []
Q = []
for v in G.vertexs:
Q.append(v)
size = len(Q)
BUILD_MIN_HEAP(Q)
while size != 0:
u = HEAP_EXTRACT_MIN(Q, size)
size = size - 1
S.append(u)
for v in u.vertexs:
RELAX(Q, size, u, v, G.edges)
if __name__ == "__main__":
s = Vertex('s')
t = Vertex('t')
x = Vertex('x')
y = Vertex('y')
z = Vertex('z')
edges = []
edges.append(Edge(s, t, 10))
edges.append(Edge(s, y, 5))
edges.append(Edge(x, z, 4))
edges.append(Edge(t, x, 1))
edges.append(Edge(t, y, 2))
edges.append(Edge(y, t, 3))
edges.append(Edge(y, x, 9))
edges.append(Edge(y, z, 2))
edges.append(Edge(z, x, 6))
edges.append(Edge(z, s, 7))
G = Graph()
INITGRAPH(G, edges)
DIJKSTRA(G, s)
DIJKSTRA算法花费由以下几个部分组成:
INITIALIZE_SINGLE_SOURCE花费 O(|V|);BUILD_MIN_HEAP花费cost_BMH;执行|V|次HEAP_EXTRACT_MIN花费|V|cost_HEM;执行|E|次RELAX花费|E|cost_RLX;而RELAX包含了一次HEAP_DECREASE_KEY花费cost_HDK;所以整个算法花费O(|V| + cost_BMH + |V|cost_HEM + |E|cost_HDK)。与最小优先队列的实现有关。直接用数组维护时花费O(|V| + |V| + |V|*|V| + |E|) = O(|V|^2),改用二叉堆维护O(|V| + |V|*lg(|V|)+ |V|*lg(|V|)+ |E|*lg(|V|)) = O((|V|+|E|)*lg(|V|))。
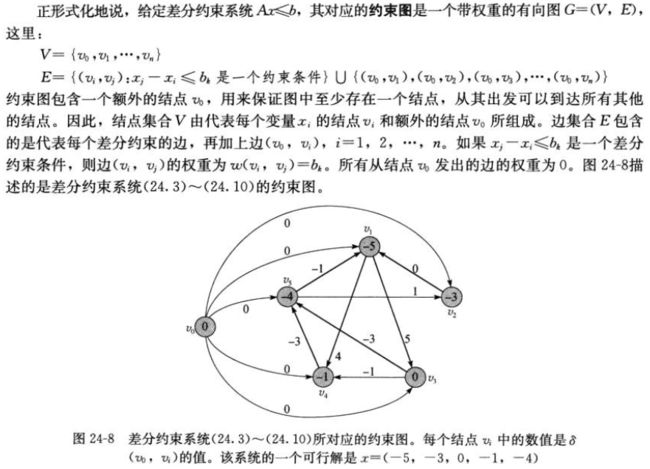
4.差分约束和最短路径
对于差分约束系统有如下定义与定理:
对于下列不等式组成的差分约束系统:
就是说之所以可以用约束图来表示差分约束系统的原因就在于可以对不等式做变形,x1 - x2 <= b ~> x1 <= x2 - b ~>使用v.d,u.d,w(u, v)来取代x1,x2, b,在形式上相同。故可以用求最短路径的方法来求解差分约束系统的解。

每次RELAX的过程就分别减小x(x1, x2...)中的xi的值以使得其解符合差分约束系统。在约束图上执行松弛的本质是在约束xj-xi <= d中,在确定xi的值的时候,降低xj使得约束成立。
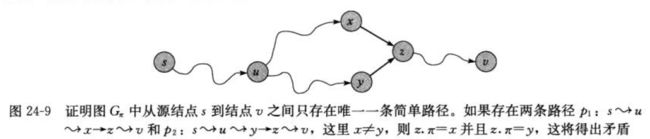
24.5 最短路径性质的证明
本章的性质证明都非常简单,课本上的反而显得啰嗦
习题解答