Pytorch权重初始化方法——Kaiming、Xavier
Pytorch权重初始化方法——Kaiming、Xavier
结论
结论写在前。Pytorch线性层采取的默认初始化方式是Kaiming初始化,这是由我国计算机视觉领域专家何恺明提出的。我的探究主要包括:
- 为什么采取Kaiming初始化?
- 考察Kaiming初始化的基础——Xavier初始化的公式
- 考察Kaiming初始化的公式
- 用Numpy实现一个简易的Kaiming初始化
为什么采取Kaiming初始化?
采取固定的分布?
当考虑怎么初始化权重矩阵这个问题时,可以想到应该使得初始权重具有随机性。提到随机,自然的想法是使用均匀分布或正态分布,那么我们如果采用与模型无关的固定分布(例如标准正态分布(均值为0,方差为1))怎么样?下面我们分析如果对模型本身不加考虑,采取固定的分布,会有什么问题:
- 如果权重的绝对值太小,在多层的神经网络的每一层,输入信号的方差会不断减小;当到达最终的输出层时,可以理解为输入信号的影响已经降低到微乎其微。一方面训练效果差,另一方面可能会有梯度消失等问题。(此处从略,参考https://zhuanlan.zhihu.com/p/25631496)
- 如果权重的绝对值太大,同样道理,随着深度的加深,可能会使输入信号的方差过大,这会造成梯度爆炸或消失的问题。
这里举一个例子,假如一个网络使用了多个sigmoid作为中间层(这个函数具有两边导数趋于0的特点):
- 如果权重初始绝对值太小,随着深度的加深,输入信号的方差过小。当输入很小时,sigmoid函数接近线性,深层模型也失去了非线性性的优点。(模型效果)
- 如果权重初始绝对值太大,随着深度的加深,输入信号的方差过大。绝对值过大的sigmoid输入意味着激活变得饱和,梯度将开始接近零。(梯度消失)
Xavier初始化
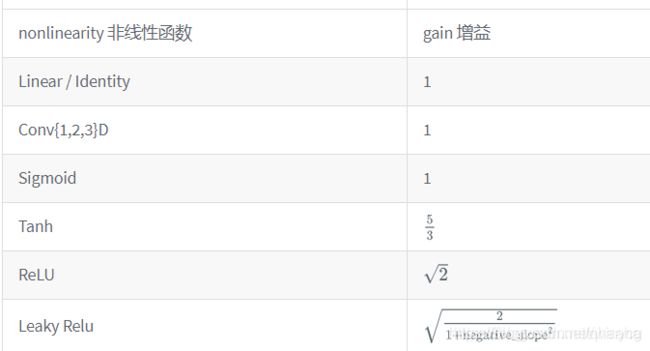
前面的问题提示我们要根据模型的特点(维度,规模)决定使用的随机化方法(分布的均值、方差),xavier初始化应运而生,它可以使得输入值经过网络层后方差不变。pytorch中这一点是通过增益值gain来实现的,下面的函数用来获得特定层的gain:
torch.nn.init.calculate_gain(nonlinearity, param=None)
增益值表(图片摘自https://blog.csdn.net/winycg/article/details/86649832)
Xavier初始化可以采用均匀分布 U(-a, a),其中a的计算公式为:
a = g a i n × 6 f a n _ i n + f a n _ o u t a = gain \times \sqrt[]{\frac{6}{fan\_in+fan\_out}} a=gain×fan_in+fan_out6
Xavier初始化可以采用正态分布 N(0, std),其中std的计算公式为:
s t d = g a i n × 2 f a n _ i n + f a n _ o u t std = gain \times \sqrt[]{\frac{2}{fan\_in+fan\_out}} std=gain×fan_in+fan_out2
其中fan_in和fan_out分别是输入神经元和输出神经元的数量,在全连接层中,就等于输入输出的feature数。
Kaiming初始化
Xavier初始化在Relu层表现不好,主要原因是relu层会将负数映射到0,影响整体方差。所以何恺明在对此做了改进提出Kaiming初始化,一开始主要应用于计算机视觉、卷积网络。
Kaiming均匀分布的初始化采用U(-bound, bound),其中bound的计算公式为:(a 的概念下面再说)
b o u n d = 6 ( 1 + a 2 ) × f a n _ i n bound = \sqrt[]{\frac{6}{(1 + a ^2) \times fan\_in}} bound=(1+a2)×fan_in6
这里补充一点,pytorch中这个公式也通过gain作为中间变量实现,也就是:
b o u n d = g a i n × 3 f a n _ i n bound = gain \times \sqrt[]{\frac{3}{ fan\_in}} bound=gain×fan_in3
其中:
g a i n = 2 1 + a 2 gain = \sqrt{\frac{2}{1 + a^2}} gain=1+a22
Kaiming正态分布的初始化采用N(0,std),其中std的计算公式为:
s t d = 2 ( 1 + a 2 ) × f a n _ i n std = \sqrt[]{\frac{2}{(1 + a ^2) \times fan\_in}} std=(1+a2)×fan_in2
这里稍微解释一下a的含义,源码中的解释为
the negative slope of the rectifier used after this layer
简单说,是用来衡量这一层中负数比例的,负数越多,Relu层会将越多的输入“抹平”为0,a用来平衡这种“抹平”对于方差的影响。
Pytorch Linear层默认初始化
pytorch的线性层进行的默认初始化的例子:
fc1 = torch.nn.Linear(28 * 28, 256)
在Linear类中通过
self.reset_parameters()
这个函数来完成随机初始化的过程,后者使用的是
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
可见是我们前面提到的Kaiming均匀分布的初始化方式,这个函数的内容和前面的公式相符(使用gain作为中间变量):
fan = _calculate_correct_fan(tensor, mode)
gain = calculate_gain(nonlinearity, a)
std = gain / math.sqrt(fan)
bound = math.sqrt(3.0) * std # Calculate uniform bounds from standard deviation
with torch.no_grad():
return tensor.uniform_(-bound, bound)
同时将参数a 的值设置为5。
使用numpy完成get_torch_initialization
简单起见,我没有按照pytorch的封装方法分层实现初始化过程,后者主要为了提供多种不同的初始化方式。我直接按照线性层默认的初始方式——Kaiming均匀分布的公式用numpy实现了get_torch_initialization,其中a值取5, 代码如下:
def get_torch_initialization(numpy = True):
a = 5
def Kaiming_uniform(fan_in,fan_out,a):
bound = 6.0 / (1 + a * a) / fan_in
bound = bound ** 0.5
W = np.random.uniform(low=-bound, high=bound, size=(fan_in,fan_out))
return W
W1 = Kaiming_uniform(28 * 28, 256, a)
W2 = Kaiming_uniform(256, 64, a)
W3 = Kaiming_uniform(64, 10, a)
return W1,W2,W3