【简单AI井字棋】
井字棋AI开发
- 1.井字棋的原理
-
- 井字棋流程图
- 井字棋实现过程
-
- 1.游戏菜单
- 2.打印棋盘
- 3.人先走
- 4.电脑先走
- 5.玩家下棋
- 6.电脑下棋
-
- 原始方法
- AI下棋
-
- 1.暴力枚举
- 2.极大极小算法
我们要开发一款AI项目,最重要的是得理解它的原理
1.井字棋的原理
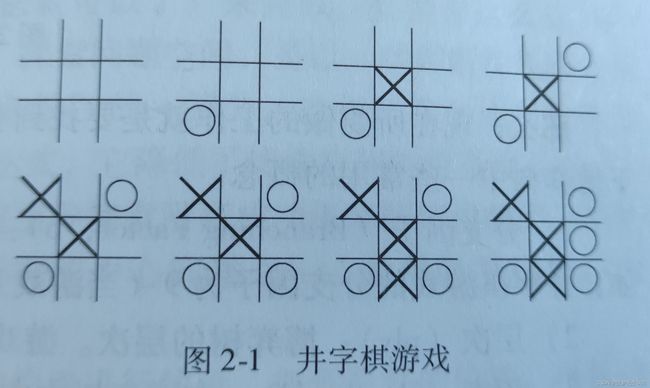
双方轮流下棋,若其中一方在水平、垂直、斜线方向上形成三个棋子连线,则获胜
井字棋流程图
井字棋实现过程
1.游戏菜单
这是一个双人游戏,自然有一个先后的问题,那么人先走和电脑先走的情况肯定是不一样的,所以我们得用switch函数将其分开来运行。
void menu()
{
printf("\n\n\n");
printf("*************************************************\n");
printf("******* ********\n");
printf("******* 欢迎使用井字棋人机对弈系统 ********\n");
printf("******* ********\n");
printf("*************************************************\n");
printf("\n\n\n");
printf("正在为您跳转,请稍后...\n");
Sleep(2000);
system("CLS");
printf("\n\n\n");
printf("**************************************\n");
printf("******* 1.PlayerFirst ********\n");
printf("******* 2.ComputerFirst ********\n");
printf("******* 0.Exit ********\n");
printf("**************************************\n");
}
2.打印棋盘
在没有下棋之前,棋盘肯定是空的,所以我们得将棋盘初始化,我们每下一次,棋盘就变化一次,因此我们还得打印一下棋盘,以便我们观察。
棋盘呢有多种形式,带边框的和不带边框的就看你喜欢哪种了,具体思路是一样的,就是细节上有略微的差异
//棋盘初始化
void Inintboard(char board[ROW][COL], int row, int col)
{
int i = 0;
int j = 0;
for (i = 0; i < row; i++)
for (j = 0; j < col; j++)
{
board[i][j] = ' ';
}
}
//打印棋盘
void Displayboard()
{
system("CLS");
int i, j;
for (i = 0; i < COL; i++)
{
printf("-------------\n");
for (j = 0; j < ROW; j++)
{
if (board[i][j] == COM)
{
printf("| X ");
}
else if (board[i][j] == MAN)
{
printf("| O ");
}
else
{
printf("| ");
}
}
printf("|\n");
}
printf("-------------\n");
}
3.人先走
void game1()
{
//存储数据--二维数组
char board[ROW][COL];
//棋盘初始化
Inintboard(board, ROW, COL);
//打印棋盘
Displayboard();
char ret = 0;
while (1)
{
//玩家下棋
PlayerMove();
Displayboard();
//判断玩家是否赢了
ret = IsWin();
if (ret != 'C')
break;
//电脑下棋
ComputerMove();
Displayboard();
//判断电脑是否赢了
ret = IsWin();
if (ret != 'C')
break;
}
if(ret == 'O')
{
Sleep(1000);
system("CLS");
printf("玩家赢了\n");
Sleep(2000);
}
else if (ret == 'X')
{
Sleep(1000);
system("CLS");
printf("电脑赢了\n");
Sleep(2000);
}
else if(ret == 'Q')
{
Sleep(1000);
system("CLS");
printf("平局\n");
Sleep(2000);
}
Displayboard();
}
4.电脑先走
void game2()
{
//存储数据--二维数组
char board[ROW][COL];
//棋盘初始化
Inintboard(board, ROW, COL);
//打印棋盘
Displayboard();
char ret = 0;
while (1)
{
//电脑下棋
ComputerMove();
Displayboard();
//判断电脑是否赢了
ret = IsWin();
if (ret != 'C')
break;
//玩家下棋
PlayerMove();
Displayboard();
//判断玩家是否赢了
ret = IsWin();
if (ret != 'C')
break;
}
if (ret == 'O')
{
Sleep(1000);
system("CLS");
printf("玩家赢了\n");
Sleep(2000);
}
else if (ret == 'X')
{
Sleep(1000);
system("CLS");
printf("电脑赢了\n");
Sleep(2000);
}
else if (ret == 'Q')
{
Sleep(1000);
system("CLS");
printf("平局\n");
Sleep(2000);
}
Displayboard();
}
5.玩家下棋
此项目中,我们用的是二维数组来制作的棋盘,所以玩家在下棋的时候只用输入需要落入棋子的坐标即可,既然是输入坐标,那么就有可能是输入错的,或者在该位置已经有棋子了,因此我们需要先判断输入坐标的合法性,如果合法了我们再判断该位置是否有棋子了。
//玩家下棋
void PlayerMove()
{
printf("玩家走\n");
int x = 0;
int y = 0;
while (1)
{
printf("请输入下棋的坐标>\n");
scanf("%d %d", &x, &y);
if (x >= 1 && x <= ROW && y >= 1 && y <= COL)
{
if (board[x - 1][y - 1] == ' ')
{
board[x - 1][y - 1] = MAN;
break;
}
else
{
printf("坐标被占用,请重新输入\n");
}
}
else
{
printf("坐标错误,请重新输入\n");
}
}
}
6.电脑下棋
原始方法
利用srand,rand函数产生1-3的随机值x和y(因此无需判断电脑下棋坐标的合法性),然后判断该位置是否有棋子了,就可以了,本质上就是把玩家下棋里玩家输入的坐标改成rand函数生成的随机值,很简单。
为啥这没有代码呢,别问,问就是博主要给你们看更高逼格的
AI下棋
针对井字棋游戏,在游戏设计过程中可按照以下基本原则进行:
1. 如果下在该位置可以赢棋,那么久下在该位置
2. 如果对手下在该位置可以赢棋,那就下在该位置
3. 如果中心位置空闲,那么下在中心位置要优于边上和角上位置
4. 如果角上位置空闲,那么下在角上位置要优于边上位置
5. 如果只有边上位置空闲,那么只能下在边上位置
在这呢,博主提供两种方法,第一种暴力枚举所有下棋的可能,然后下棋,第二种通过极大极小搜索算法找到每次下棋的最优解,然后下棋。
1.暴力枚举
此种方法有局限性,只能是电脑先手,才能做到肯定赢棋,最差也是平局的局面,如果是人先手的话,人的下棋有9种可能,暴力枚举的次数太多,这就没必要了,这就是枚举的局限性。
//电脑下棋
void ComputerMove(char board[ROW][COL], int row, int col)
{
int x = 0;
int y = 0;
int ret = CountNum(board, row, col);
while (1)
{
if (ret == 1|| ret == 3 || ret == 5 || ret == 7)
{
x = rand() % row;
y = rand() % col;
if (board[x][y] == ' ')
board[x][y] = 'X';
break;
}
}
if (ret == 0)
{
board[0][0] = 'X';
}
if (ret == 2)
{
//5 types , 8 situations
// 1
if (board[0][1] == 'O')
{
board[2][0] = 'X';
}
// 2
if (board[1][0] == 'O')
{
board[0][2] = 'X';
}
// 3
if (board[0][2] == 'O')
{
board[2][2] = 'X';
}
// 4
if (board[2][0] == 'O')
{
board[2][2] = 'X';
}
// 5
if (board[2][1] == 'O')
{
board[2][0] = 'X';
}
// 6
if (board[1][2] == 'O')
{
board[0][2] = 'X';
}
// 7
if (board[1][1] == 'O')
{
board[0][1] = 'X';
}
// 8
if (board[2][2] == 'O')
{
board[0][2] = 'X';
}
}
if (ret == 4)
{
// 1@1
if (board[0][1] == 'O' && board[2][0] == 'X')
{
if (board[1][0] == 'O')
{
board[2][2] = 'X';
}
else
{
board[1][0] = 'X';
}
}
// 2@1
if (board[1][0] == 'O' && board[0][2] == 'X')
{
if (board[0][1] == 'O')
{
board[2][2] = 'X';
}
else
{
board[0][1] = 'X';
}
}
// 3@1
if (board[0][2] == 'O' && board[2][2] == 'X')
{
if (board[1][1] == 'O')
{
board[2][0] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 4@1
if (board[2][0] == 'O' && board[2][2] == 'X')
{
if (board[1][1] == 'O')
{
board[0][2] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 5@1
if (board[2][1] == 'O' && board[2][0] == 'X')
{
if (board[1][0] == 'O')
{
board[0][2] = 'X';
}
else
{
board[1][0] = 'X';
}
}
// 6@1
if (board[1][2] == 'O' && board[0][2] == 'X')
{
if (board[0][1] == 'O')
{
board[2][0] = 'X';
}
else
{
board[0][1] = 'X';
}
}
// 7@1
if (board[1][1] == 'O' && board[0][1] == 'X')
{
if (board[0][2] == 'O')
{
board[2][0] = 'X';
}
else
{
board[0][2] = 'X';
}
}
// 8@1
if (board[2][2] == 'O' && board[0][2] == 'O')
{
if (board[0][1] == 'O')
{
board[2][0] = 'X';
}
else
{
board[0][1] = 'X';
}
}
}
if (ret == 6)
{
// 1@1@1
if (board[0][0] == 'X' && board[2][0] == 'X'
&& board[2][2] == 'X' && board[0][1] == 'O'
&& board[1][0] == 'O')
{
if (board[1][1] == ' ')
{
board[1][1] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 2@1@1
if (board[0][0] == 'X' && board[0][2] == 'X' &&
board[2][2] == 'X' && board[0][1] == 'O' &&
board[1][0] == 'O')
{
if (board[1][1] == ' ')
{
board[1][1] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 3@1@1
if (board[0][0] == 'X' && board[2][0] == 'X' &&
board[2][2] == 'X' && board[0][2] == 'O' &&
board[1][1] == 'O')
{
if (board[1][0] == ' ')
{
board[1][0] = 'X';
}
else
{
board[2][1] = 'X';
}
}
// 4@1@1
if (board[0][0] == 'X' && board[0][2] == 'X' &&
board[2][2] == 'X' && board[2][0] == 'O' &&
board[1][1] == 'O')
{
if (board[0][1] == ' ')
{
board[0][1] = 'X';
}
else
{
board[1][2] = 'X';
}
}
// 5@1@1
if (board[0][0] == 'X' && board[2][0] == 'X' &&
board[0][2] == 'X' && board[1][0] == 'O' &&
board[2][1] == 'O')
{
if (board[0][1] == ' ')
{
board[0][1] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 6@1@1
if (board[0][0] == 'X' && board[0][2] == 'X' &&
board[2][0] == 'X' && board[0][1] == 'O' &&
board[1][2] == 'O')
{
if (board[1][0] == ' ')
{
board[1][0] = 'X';
}
else
{
board[1][1] = 'X';
}
}
// 7@1@1
if (board[0][0] == 'X' && board[0][1] == 'X' &&
board[2][0] == 'X' && board[1][1] == 'O' &&
board[0][2] == 'O')
{
if (board[1][0] == 'O')
{
board[1][2] = 'X';
}
else
{
board[1][0] = 'X';
}
}
// 8@1@1
if (board[0][0] == 'X' && board[0][2] == 'X' &&
board[2][0] == 'X' && board[0][1] == 'O' &&
board[2][2] == 'O')
{
if (board[1][0] == ' ')
{
board[1][0] = 'X';
}
else
{
board[1][1] = 'X';
}
}
}
if (ret == 8)
{
//7@1@1@1
if (board[0][0] == 'X' && board[0][1] == 'X' &&
board[1][2] == 'X' && board[2][0] == 'X' &&
board[0][2] == 'O' && board[1][0] == 'O' &&
board[1][1] == 'O')
{
if (board[2][1] == 'O')
{
board[2][2] = 'X';
}
else
{
board[2][1] = 'X';
}
}
}
}
2.极大极小算法
为方便表达游戏的状态,通常使用树或图来表达
- 分支因子:指从游戏起始出发游戏者可以移动到的位置。例如井字棋的分支因子为9(游戏开始时,下棋共有9个位置可以选择)
- 层次:博弈树的层次。游戏者通过下棋进入博弈树的下一层次。
- 深度:在博弈树中向下搜索的层次称为深度(或搜索深度)。例如井字棋游戏的搜索深度一般为6~7,而国际象棋的通常要达到40。
最重要的就是估值函数,估值函数的能力真正决定了你所写的AI的能力,估值函数判断的越准确,AI越能找到最优解。
估值函数并不是唯一的,不同的人有不同的想法,用的编程语言也不相同,所写出来的估值函数也就不一样,所以下面我就展示伪码来体现一种估值函数,希望读者能有所感悟,能写出更好的估值函数
function eval()
{
int temp[9] = 0
for i:0 to 8
temp[i] = board[i]
int win = 0
int lose = 0
for i:0 to 8
int sum = 0
for j:0 to 2
sum += temp[line[i][j]]
if(sum == 3)
then return MAX = +INFINITY
else if (sum == -3)
then return MIN = -INFNINTY
else if (-3<sum<0)
then lose ++
else if(0<sum<3)
then win ++
endif
return win-lose
}
估值函数的不同,写出来的极大极小搜索算法也不同,下面我也仅通过伪码来展示极大极小搜索算法
function minmaxSearch()
{
int bestMoves[9] = { 0 }
index = 0
int bestValue = -INFINITY
if (depth == 0 and isFull())
then return eval()
else
for pos:0 to 8
if(board[pos] == NULL)
then board[pos] = MAX
int value = minSearch(depth-1)
if(value>bestValue)
then bestValue = value
int index = 0
bestMoves[index] = pos
else if (value == bestValue)
then bestMoves[++index] = pos
endif
board[pos] = NULL
endif
endif
return bestMoves[index]
}
上述例子才用的是一维数组表示棋盘,在打印棋盘时每打印3个数据就换行,这样就保证了棋盘的正常展示,根据实际需要也可以用二维数组,改一改过程即可
还有一个十分重要的算法:阿尔法-贝塔剪枝算法,在搜索过程中,我们会发现,当搜索到一定程度时,下面的结果都不能取得最优解了,继续搜索下去,就会造成时间的浪费,因此就要把他cut掉,这就诞生了剪枝算法
但由于井字棋的搜索树并不大,搜索时间也不多,所以是用不到阿尔法-贝塔剪枝算法的。这里就不继续阐述了。
至此,井字棋AI介绍就完了,你get到了吗?

