论文研究 | 多车道线检测和分类算法—基于滤波图像，多个约束因子，叠加角度直方图和截距约束等

       机器视觉目前的应用场景很多，道路缺陷检测是其中比较典型的，目前做道路缺陷检测的机器视觉企业有很多，但是精度一直不太高，而且道路情况限制很多。

       在知网上看到了这种新的方法，想和大家一起分享一下。  

 

0 引言

略。

1 图像预处理

本文算法以车载摄像头在某主干道行驶中拍摄到的图像作为检测对象，采集到的图像如图 1a）所示。为提高检测效率并将多车道线的信息保留下来，需进行预处理。行驶中拍摄到的天空区域无疑是无效检测区域，故对图像高度进行裁剪但不改变宽度，留下图像下方1/3 的区域作为有效检测区域（感兴趣区域），如图 1b）所示。

 为在提取出车道线特征信息时减小干扰，使用 c=1 和 γ=3 的 Gamma 校正对图像进行增强；同时，为避免因Gamma 校正引起车道线本身颜色灰度值变小而不对高阈值像素进行变换，如公式（1）所示：

 式中：gray 为校正前的值；r 为 gray 经归一化后的值；s 为校正后的值；c和 γ为正常数。增强后的图像如图 2a）所示，然后使用 Canny 边缘检测算法得到边缘图像如图 2b）所示。

 2 多相位 Gabor滤波图像

Gabor 是联合空间域和频率域的一种纹理分析方法，它能够考虑信号在空间域和频率域上的关系并能取得局部最优[19]。利用车道线的纹理走向，Gabor 滤波器可以提取所需方向的纹理。使用一个高斯函数和一个余弦函数相乘来模拟其特性，如公式（2）所示：

 其中：x′ = xcos θ + ysin θ；y′ = -xsin θ + ycos θ。

式中：x 和 y 为图片像素的坐标；λ 为余弦因子的波长； θ 为滤波的方向；ψ 表示相位偏移量；σ 表示高斯函数的标准差；ζ表示长宽比。

提取多车道线的纹理分为两个步骤：构造 Gabor 滤波器（核）和使用滤波器（核）对图像进行滤波（卷积）。

在角度区间 π 内以步长 π 12产生 12个不同方向的Gabor滤波核，核函数的效果图如图 3所示。

使用 Gabor 滤波和高斯滤波反复滤波直至所有车道线都清晰，对滤波后的图像进行二值化变换，变换后的滤波图如图 4所示，对滤波结果分析如表 1所示。

左右车道按照最佳相位区间将多张相位图进行和运算合成左右车道图，取左车道图的左半部分和右车道图右半部分水平拼接合成多相位 Gabor 叠加滤波图，如图 5所示。

 3 多车道线分类

使用聚类或生长的方法完成多车道线分类虽易于实现，但难以将混一起的车道线区分，同时计算时间成本过高无法满足实时性，若将图像下采样处理又会丢失信息。

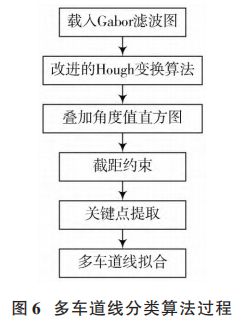
对此提出一种分类方法，过程如图 6 所示，分为两个阶段进行处理。先利用改进的 Hough 变换对 Gabor叠加滤波图进行直线段提取；再基于叠加角度值直方图和截距约束的方法实现多车道线快速分类；最后提取出线段上少量关键点拟合出所有车道线。

3.1 改进的 Hough变换算法

直接使用标准 Hough 变换会因为边缘图像中某些像素的缺失导致识别出许多一段段的小直线，缺少了“连续性”；同时“连续性”的丢失进一步导致了识别不到车道线的短虚线，因此需要对原有的 Hough 变换添加约束因子，使提取的线段满足需求。

在原有算法上增加 Ta，Lmin，LG 和 Aa 四个变量参数。 Ta 表示检测到点最少数量的阈值；Lmin 为识别到线段的最小像素长度阈值；LG 为允许的最大间隔阈值，使识别到的直线具有连续性，不因某个点的缺失导致线段丢失；Aa 为角度阈值约束，保证所识别线段的角度满足车道线角度特征出现的范围。当同时满足以上所有阈值限制的线段才保留下来。直接使用标准 Hough 变换对原图像提取直线效果如图 7a）所示，对 Gabor 叠加滤波图使用 Hough 变换效果如图 7b）所示，使用本文算法对叠加滤波图提取效果如图 7c）所示。

 从图 7a）和图 7b）中可知：Gabor 滤波有很好的方向滤波效果，让属于车道线纹理走向特征保留下来，但线段不连续且杂乱多；而本文方法保证识别结果连续的同时，还过滤如护栏等非车道线信息。

3.2 多车道线快速分类

随着车道线数量增多，车道线角度值相差很小且同一角度值的线段出现在不同车道线上，导致区分开每一条线段所属的车道线较为困难。以车辆右边的车道线为例，对车道线段的角度值取整后建立直方图，如图 8所示。直方图的形状可体现所隐藏的信息，若直方图出现多个峰形，是由于观测值来自多个总体、多个分布的数据混合在一起造成。考虑到实际角度相差小难以区分，对角度值相差为 1°的线段进行叠加，每一区间内的最高峰所对应的角度值认为是该车道线的主角度值，在低角度区间因多条车道线叠加在一起而出现多个高峰。

 

未经过累加时，在低角度值区域（10°~16°）表现出折齿型，说明数据混淆在一起造成的，例如双线（虚实线）和路沿之间相差仅 1°，同一角度值的线段出现在不同车道线上。累加后该区间变成双峰型，可在其中提取出峰值对应的角度作为车道线的主角度值。为区分混淆在一起具有相同角度但不属于同一条车道线的线段[20]，使用双截距约束。

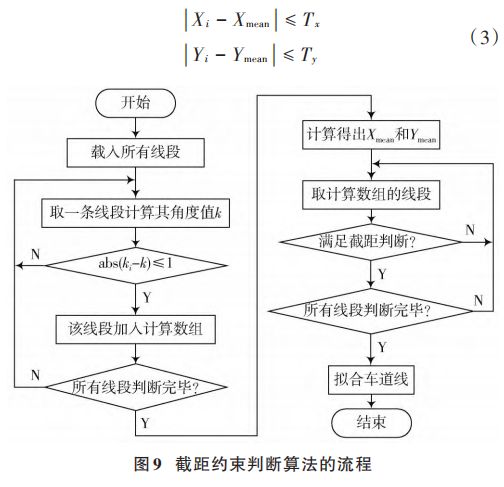
设主角度值为 k（i i=1，2，…），取与 ki相差 1°的线段，求得这些线段在 x 轴、y 轴上的截距为 Xi 和 Yi，剔除最大值和最小值后求平均值为 Xmean 和 Ymean。当线段截距与

平均截距的绝对值距离小于阈值 Tx 和 Ty 时，如公式（3） 所示，认为该线段属于该车道线上的线段，具体流程如图 9所示。

若直接使用双截距约束判断而不经叠加图寻找主角度值，每一个角度值都需计算，计算量不能满足实时检测的需求。线段分类后提取每条车道线所属的线段端点和中心点，使用最小二乘法进行拟合，中心点的加入可保证大于一次方拟合时不会出现 S 形曲线。拟合车道线时根据识别到线段的欧几里德像素距离区分实线和虚线，拟合后的图像如图 10a）所示。

 行车记录仪采集到的图像为 25 f/s，正常行驶时有效检测区域的变化在一定的范围之内，不会突变。因此可提取出最外车道线的关键点，并向外延伸 10 个像素点作预留变化的区间，围成的区域作为动态有效检测区域，剪切后图像如图 10b）所示。

4 实验结果和分析

本文算法的实现基于PyCharm编译平台，编程语言为Python 3.6，操作系统为 Windows 10 64 bit，CPU 主频为3.10 GHz。实验对车道线识别能力和泛化能力进行测试。

首先在 Tusimple 数据集中选取图像 1 800 张，共有7 200 条车道线。分别使用颜色阈值法、鸟瞰图法和基于 Gabor 滤波器检测法进行对比，统计多车道线检测的漏检率、误检率和准确率统计结果见表 2。其中：准确是指无漏检、无误检的图像；漏检是没有被识别出的图像；误检是指将非车道线（例如路沿和缩缝等）误认为是车道线的图像。在同一张图中可能会同时存在漏检和误检两种情况。

 检测结果如图 11a）所示，其中数字为识别图像序号，Ⅱ~Ⅴ分别为算法 1~3 和本文算法的检测图，Ⅵ为拟合图像。

从表 2 中可得出，本文算法相较于其他算法，漏识率和误检率较低，准确率更高。算法 1 利用车道线的颜色区间因此误检的情况较少，但过分依赖颜色阈值区间导致识别多车道线时非本车道以外漏识较多。算法 2虽然把多车道线识别出来，但更多的时候识别出来的是非车道线信息，因此误检导致整体准确率不高，同时也受障碍物的遮挡和逆变后的有效信息变形导致漏识。算法 3 利用车道线的纹理方向，在一定情况下能完成多车道线的识别；但随着车道线数量的增多，导致多车道线信息丢失而识别能力下降，同时过分依赖纹理走向将路面的缩缝等认作为车道线，实际上得到的结果是错误的，如图 11a）的（3.Ⅳ）所示。上述算法存在漏检和误检的原因是在处理时忽略多车道线在拍摄时不清晰，同时又过分关注某一特征，最后未能识别出全部车道线信息导致准确率降低。本文算法在预处理时对车道线进行增强，多相位的 Gabor滤波叠加后保留多车道线信息，如图 11a）的（3.V）所示；使用改进后的 Hough变换抑制散乱的线段，叠加角度直方图能区分叠加的车道线信息。

为验证本文算法的泛化能力，在实际驾驶某主干道路拍摄到的视频中选取拥挤和夜间两种情况各 1 800帧加以验证，车道线检测结果如图 11b）所示。

 图 11 中，Ⅰ为有效检测区域，Ⅱ为本文算法检测图像，Ⅲ为拟合结果。复杂情况检测评估如表 3所示。

 

在拥挤环境里其他车辆的行驶遮挡车道线，距离较远的车道线因车速或拍摄不清晰等原因必然降低车道线信息，在识别前需对其进行增强，同时识别的难度也增加；夜间环境较暗，车道线与背景的梯度较小且较为模糊，易受光线照射的影响，因此识别难度大。从图 11b）可看出，使用本文算法在各种复杂情况下均能识别出多车道线，具有一定的鲁棒性。

5 结 语

本文首先对图像进行裁剪有效检测区域、Gamma校正和像素值增强等预处理，目的在于突出梯度的同时保证多车道线信息不丢失；然后基于多相位 Gabor 滤波器进行滤波叠加合成 Gabor 滤波叠加图，留下与车道线相关的纹理信息；接着使用多变量因子的 Hough 变换算法将车道线转化为多条直线段，减少无关干扰；最后基于叠加直方图和双截距约束的方法实现快速分类。通过少量关键点完成拟合。存在时间上下文联系的数据集中增加动态有效检测区域，提高检测的准确率，减少检测时间成本。

与传统的算法相比，本文算法主要有以下优点：

一是适用性更好，考虑到实际驾驶遇到的情况，不因颜色和类似车道线的线段干扰（例如缩缝、路沿等）造成误识和漏识，也能够区分开双线的情况；

二是鲁棒性好，在拥挤和夜间的行驶环境下也有较高的准确率。

但本文算法仍存在不足之处，对于车辆变道时如何做到及时更新算法判断条件，在某一段时间内车道线被遮挡或完全消失或突然增多的情况下如何识别等问题仍需要深入研究，在接下来的研究中可以将多车道拟合结果融入更复杂的环境中。

6 参考文献

略。

---

文章来源：朱贤臻，魏霞，黄德启. 基于机器视觉的多车道线检测和分类算法 [J]. 现代电子技术, 2022,45(23)