谱聚类算法详解

  谱聚类（Spectral Clustering）算法简单易行，其聚类性能优于传统的K-means算法。谱聚类将数据的划分转化为对图的分割，是一种基于图论的聚类方法，其直观理解为根据图内点的相似度将图分为多个子图，使子图内部的点相似度最高，子图之间点的相似度最低。

1. 图论基础

1.1 图的表示

  记 G=(V,E) 表示一个无向加权图， V 表示所有顶点的集合V={v1,...,vn}， E 表示所有边的集合，并且任意两点vi和 vj 的边具有非负权值 wij≥0 。图的邻接矩阵为 W=(wij)i,j=1,...,n ，如果 wij=0 则表示点 vi 和 vj 之间没有连接。由于 G 为无向图，所以其邻接矩阵具有对称性，即wij=wij。图中任一点 vi 的度为 di=∑nj=1wij ，表示一个点与其他所有点的连接情况，图的度矩阵 D 为每个点的度所构成的对角矩阵D=diag{d1,...,dn}。

1.2 相似度图的构造方法

  给定一组数据集 V={v1,...,vn} ，将其构造为相似度图的意义在于描述点对之间的局部近邻关系。此处介绍三种构造相似度图的方法。
  （1）ε近邻图。如果两点之间的距离小于给定值ε，则连接两点。ε的值需要根据图中各点的距离选择，使与某一点连接的点不会太多，也不会太少。
  （2） k 近邻图。如果点vj是 vi 的 k 近邻点之一，则连接两点。由于近邻点的非相互性，按此方法构造的邻接矩阵不对称，一种方法是采取“或”的方式，即如果vj是 vi 的 k 近邻点之一，或vi是 vj 的 k 近邻点之一，则连接两点；另一种方法是采取“与”的方式，如果vj是 vi 的k近邻点之一，并且 vi 是 vj 的k近邻点之一，则连接两点。
  （3）全连接图。不考虑任何因素，直接将所有的点两两相连，由于图表示点之间的局部邻接特性，常用的相似性函数为 s(xi,xj)=exp(−∥xi−xj∥22σ2) 。

1.3 图的Laplacian矩阵

  这里我们要讲到谱聚类中的关键内容——拉普拉斯矩阵，其定义为 L=D–W ，其中 D 和W就是上文定义的图的度矩阵和邻接矩阵。下面我们给出谱聚类中用到的拉普拉斯矩阵的一些性质。
  （1）对任意的向量 f∈Rn ，有 fTLf=12∑i,j=1nwij(fi−fj)2 。
  证明：（此处用到了W的对称性）

fTLf=fTDf−fTWf=∑i=1nf2idi−∑i,j=1nwijfifj=∑i,j=1nwijf2i−∑i,j=1nwijfifj=12⎛⎝∑i,j=1nwijf2i+∑i,j=1nwijf2j⎞⎠−∑i,j=1nwijfifj=12∑i,j=1nwij(fi−fj)2

（2） L 是对称半正定矩阵，该性质可由（1）直接得到。
（3）L 的最小特征值为 0 ，对应的特征向量为常数向量1 ，即 L 的行和或列和为0 。
（4）本文假设 L 的特征值按照从小到大的顺序排列，0=λ1≤...≤λn 。
  此外，还有normalized Laplacian，分别定义为
Lsym=D−12LD−12=I−D−12WD−12 ，和 Lrm=D−1L=I−D−1W ，其中两个下标sym和rw分别代表symmetric和random walk，此处不再介绍这两个矩阵的性质。

2. 谱聚类算法

2.1 图的分割问题

  谱聚类算法源于图的分割（cut），首先将所有的样本点连接成图，然后将图分割成不同的子图，使得不同子图之间的连接权值最小。
  定义两个子图之间的连接权值为 W(A,B)=∑i∈A,j∈Bwij ，记 A¯¯¯ 为 A 的补集，为了表达方便，我们记vi∈A为 i∈A 。如果将图分割为 k 个子图A1,...,Ak，那么最优分割问题可通过最小化如下表达式来实现：

cut(A1,...,Ak)=12∑i=1kW(Ai,Ai¯¯¯¯)

   然而，此优化问题通常不能生成有效的分割，它会将图中的一个点与其余 n−1 个点分割开来，如下图所示，导致图的分割不均衡。

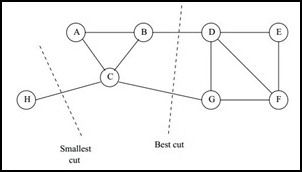
解决该问题的有效办法是让每个子图都有合理的大小，子图大小的度量方式不同就会得出不同的最小分割问题，常用的两种方法是RaioCut和Normalized Cut，分别如下：
RatioCut(A1,...,Ak)=12∑i=1kW(Ai,Ai¯¯¯¯)|Ai|=∑i=1kcut(Ai,Ai¯¯¯¯)|Ai|
Ncut(A1,...,Ak)=12∑i=1kW(Ai,Ai¯¯¯¯)vol(Ai)=∑i=1kcut(Ai,Ai¯¯¯¯)vol(Ai)
这两个目标函数均将子图的大小作为分母，这样就可以使每个子图不会太小，其中RatioCut以子图中点的个数 |Ai| 作为子图大小的度量，Normalized Cut以子图内所有点的度的和作为子图大小的衡量，即 vol(Ai)=∑j∈Aidj 。
  下面我们分别讨论RatioCut和Normalized Cut是如何通过谱聚类来求解的。

2.2 求解RatioCut

  首先从二聚类问题开始分析，其目标函数为最小化

RatioCut(A,A¯¯¯)=cut(A,A¯¯¯)(1|A|+1|A¯¯¯|)
定义向量 f=(f1,...,fn)T∈Rn ，其每个元素的定义如下：
fi=⎧⎩⎨⎪⎪|A¯¯¯|/|A|−−−−−−√−|A|/|A¯¯¯|−−−−−−√ifvi∈Aifvi∈A¯¯¯
结合图的Laplacian矩阵，我们可以得到RatioCut问题，推导过程如下：

fTLf=12∑i,j=1nwij(fi−fj)2=12∑i∈A,j∈A¯wij⎛⎝∣∣A¯∣∣|A|−−−√+|A|∣∣A¯∣∣−−−√⎞⎠2+12∑i∈A¯,j∈Awij⎛⎝−∣∣A¯∣∣|A|−−−√−|A|∣∣A¯∣∣−−−√⎞⎠2=12∑i∈A,j∈A¯wij⎛⎝∣∣A¯∣∣|A|+|A|∣∣A¯∣∣+2⎞⎠+12∑i∈A¯,j∈Awij⎛⎝∣∣A¯∣∣|A|+|A|∣∣A¯∣∣+2⎞⎠=12⎛⎝∑i∈A,j∈A¯wij+∑i∈A¯,j∈Awij⎞⎠⎛⎝∣∣A¯∣∣|A|+|A|∣∣A¯∣∣+2⎞⎠=cut(A,A¯)⎛⎝∣∣A¯∣∣+|A||A|+|A|+∣∣A¯∣∣∣∣A¯∣∣⎞⎠=|V|cut(A,A¯)⎛⎝1|A|+1∣∣A¯∣∣⎞⎠=|V|RatioCut(A,A¯)
其中， |V| 表示所有点的个数，给定样本点后， |V| 是个常数。
  因为，求解RatioCut问题可以转变为最小化 fTLf 的问题，其中 f 的取值如上面所定义，然而，该离散优化问题是NP-hard，因此，我们将其进行松弛，使fi能够取任意实数。同时，为了和原问题尽量保持一致，我们加入 f 的两个约束，f⊥1→和 ∥f∥=n−−√ ，这两个约束可从 f 的定义得到。最后，二聚类问题就转化成了有约束的优化问题：

minf∈RnfTLfs.t.f⊥1→,∥f∥=n−−√
根据Rayleigh-Ritz定理可知，该问题的解为Laplacian矩阵 L 的最小特征值所对应的特征向量，由于L 的最小特征值为 0 ，对应的特征向量为常数向量1 ，不满足约束条件，因此，应取第 2 小的特征值所对应的特征向量。
  求解上述优化问题后，要将数据集分为2 个簇，我们可简单地采取如下的方式：

{vi∈Avi∈(¯A)iffi≥0iffi<0

  上述的二聚类问题可以很容易地推广到 k 聚类问题，如果将一个数据集分为k 个子集 Ai,...,Ak ，首先定义 k 个示性向量H=(h1,...,hk)T ，其中

hij={1/|Aj|−−−−√0ifvi∈Ajotherwise,i=1,...,n;j=1,...,k

由该定义可知， H 的列相互正交，即HTH=I。类似上面的推导（此处不再给出详细过程）：

hTjLhj=cut(Aj,Aj¯¯¯¯)|Aj|
此外， hTjLhj=(HTLH)jj ，因此

RatioCut(A1,...,Ak)=∑j=1khTjLhj=∑j=1k(HTLH)jj=Tr(HTLH)
所以，多聚类的RatioCut问题可以转化为最小化 Tr(HTLH) 的问题， H 的取值如上面所定义。同样，我们将该NP-hard问题松弛，使H 的元素取任意实数，松弛问题就变为：

minH∈Rn×kTr(HTLH),s.t.HTH=I
这是标准的迹最小化问题，其解为 L 的的前k 个特征向量所构成的矩阵。最后采用k-means方法对该矩阵的行进行聚类，就可以实现对该数据集的 k 聚类。

2.3 求解Normalized Cut

  类似于RatioCut，下面我们简要给出Normalized Cut的实现过程。
  首先分析二聚类的情况，定义示性函数如下：

fi=⎧⎩⎨⎪⎪vol(A¯¯¯)/vol(A)−−−−−−−−−−−√−vol(A)/vol(A¯¯¯)−−−−−−−−−−−√ifvi∈Aifvi∈A¯¯¯
按照该定义， f 具有性质(Df)T1→=0 和 fTDf=vol(V) ，并且可以证明 fTLf=vol(V)Ncut(A,A¯¯¯) ，加上松弛条件，使 f 可以取任意实数向量，Normalized Cut可以转化成有约束的优化问题
minf∈RnfTLf,s.t.Df⊥1→,fTDf=vol(V)
  该问题需要求解广义特征向量问题 Lf=λDf ， f 取L 的第二小的广义特征值对应的特征向量。
  再扩展到 k 聚类问题，定义k 个示性向量 H=(h1,...,hk)T ，其中

hij={1/vol(Aj)−−−−−−√0ifvi∈Ajotherwise,i=1,...,n;j=1,...,k
按照该定义， H 具有性质hTjDhj=1 ，那么 HTDH=I ，并且可以证明

hTjLhj=cut(Aj,Aj¯¯¯¯)/vol(Aj)
因此， Ncut(A1,...,Ak)=Tr(HTLH) ，加上松弛条件，使 H 的元素可以取任意实数，Normalized Cut就可以转化为如下有约束的优化问题：

minH∈Rn×kTr(HTLH)s.t.HTDH=I
该问题的解为广义特征值问题 Lh=λDh 的前 k 个特征向量所构成的矩阵。最后采用k-means方法对该矩阵的行进行聚类，就可以实现对该数据集的k 聚类。

2.4 小结

  针对以上两种图分割方法，谱聚类算法的步骤如下：
  Step1：将每个样本看做图的顶点，构造无向加权图；
  Step2：计算图的邻接矩阵W和拉普拉斯矩阵L；
  Step3：根据图的分割准则计算拉普拉斯矩阵的前k个特征向量；
  Step4：将拉普拉斯矩阵的前k个特征向量构成矩阵Y，把Y的每一行看做一个样本，然后用k-means方法对Y进行聚类。

3. 总结

  谱聚类相当于先进行非线性降维，使原始数据点能够线性可分，最后再使用k-means聚类就可以得到比较好的聚类效果。
  谱聚类算法也存在以下几点不足：
  （1） 谱聚类的松弛条件是对原问题的一个近似，但是并不能保证该近似是合适的，其误差有可能非常大，而且导致聚类问题不稳定；
  （2） 构造相似度矩阵的尺度参数根据经验设定，尺度参数的选择对聚类效果影响较大；
  （3） 同其他聚类方法一样，聚类数目的选择难以确定；
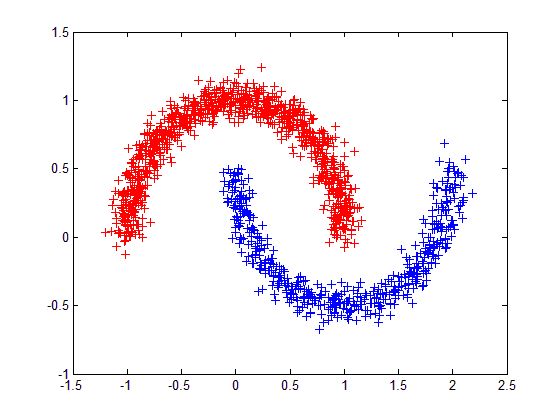
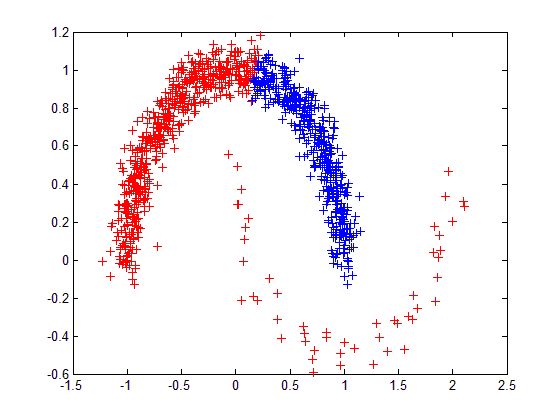
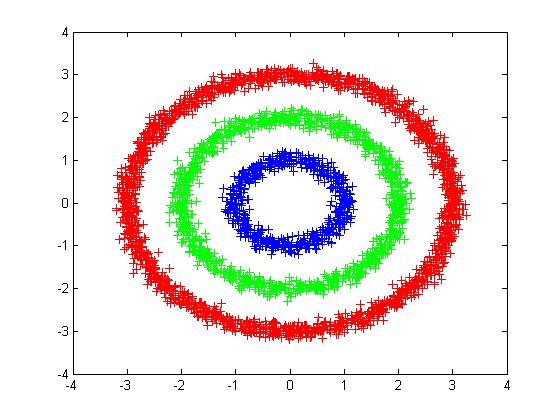
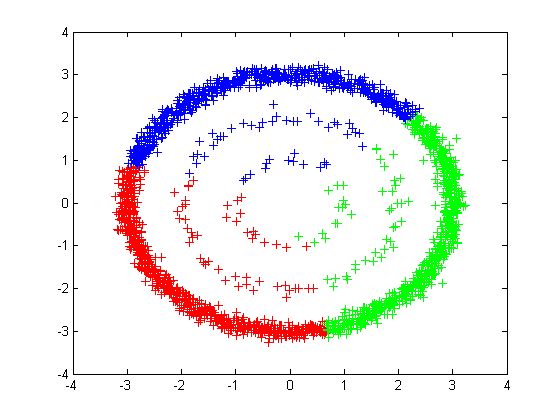
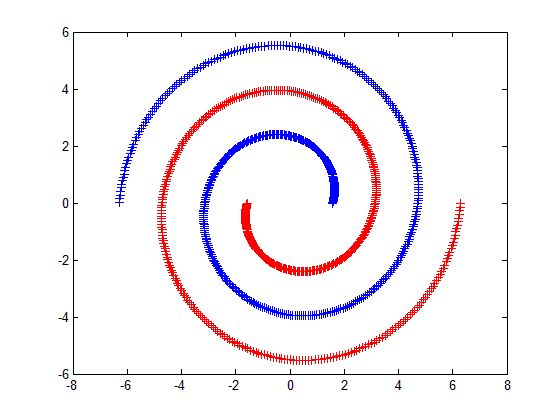
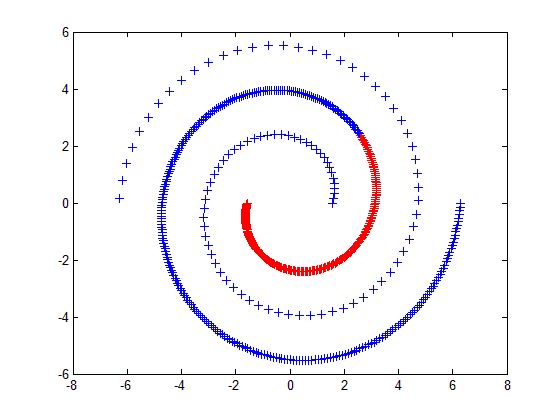
  （4） 根据图最小分割的目标函数可知，谱聚类适用于均衡分类问题，即各簇之间点的个数相差不大，对于簇之间点个数相差悬殊的聚类问题，谱聚类则不适用。
  以下一组图均为采用谱聚类方法进行聚类的结果，左侧一列的数据点个数分布比较均衡，聚类效果比较好，可以看出，右侧一列数据点的分布不均衡，谱聚类算法仍然将数据分成几个均衡的簇，而不能体现数据的分布结构。