Solving Linear Inverse Problems Using The Prior Implicit in a Denoiser (Paper reading)

Solving Linear Inverse Problems Using The Prior Implicit in a Denoiser (Paper reading)

Zahra Kadkhodaie, New York University, NeurIPS2020 Workshop Deep Inverse, Cited:28, Code, Paper

1. 前言

目前的有监督的基于神经网络的方法并没有明确的利用图像的先验。相比于传统方法来说，深度学习方法能够嵌入更多的先验知识。但是这些隐式先验是由训练数据的分布、网络架构、优化目标中包含的正则化项和优化算法的组合产生的。此外，它们与优化它们的任务交织在一起。之前的方法使用嵌入到降噪器中的先验来解决其他逆问题。（那么处了利用去噪器中的先验知识，是否还可以利用其他的先验知识呢？比如大型的预训练模型？）本文提出了一个通用的算法，用去噪器隐式先验解决线性可逆问题(linear inverse problems)。我们从经典统计的结果出发，发现在最小化被加性高斯噪声破坏的图像的平方误差的降噪器可以解释为计算噪声图像密度对数的梯度，也就是说该结果表明了分数函数(score function)与 MMSE 降噪器之间的极有价值的联系，对inverse问题应用扩散模型理论提出了一个非常具有价值的想法。本文使用预训练的最先进的 CNN 图像降噪器中的先验隐式，在图像合成、修复、超分辨率、去模糊和丢失像素恢复方面产生高质量的结果。

2. 整体思想(个人理解)

算法的整体思想就是，给定一个随机的初始分布，我们通过迭代不断的沿着先验知识的方向，也就是梯度方向，最终我们可以走到目标样本密集的地方，这时候的收敛得到的$y_t$就可以近似为真实分布的采样。因为我们的预训练去噪器学习了大量的先验知识，因此算法没训练过程，直接给$y_0$迭代就可以生成图像。

3. 方法

假设噪声观测图像$y=x+z$，其中$z\sim N(0,{\sigma }^{2}I)$，$x\in R^N$是从原始图像分布$p(x)$中提取的。观测的密度$p(y)$通过边缘化与先验$p(x)$建立联系：
$$p(y)=\int p(y|x)p(x)dx=\int g(y-x)p(x)dx\text{\hspace{1em}(1)}$$
公式(1)可以看作卷积的形式，这里假设$p(y|x)$是噪声强度为${\sigma }^2$的高斯分布，形势如下，因此$p(y)$是先验分布$p(x)$的高斯模糊版本。此外，不同噪声方差的观测密度族$p_{\sigma }(y)$形成了高斯尺度空间的先验表示，类似于扩散过程的时间演化。
$$g(z)=\frac{1}{(2\pi {\sigma }^2{)}^{N/2}}{e}^{-||z|{|}^2/2{\sigma }^2}$$

假设我们有一个训练有素的 CNN 降噪器，其嵌入了图像结构的详细先验知识。给定这样一个降噪器，我们如何才能访问这个隐式先验？最近的结果得出了分数匹配密度估计和去噪之间的关系，并使用这些关系来利用隐式先验信息，就如NCSN。在这里，我们利用经验贝叶斯估计文献中的一个更直接但鲜为人知的结果，在高斯噪声的前提下，最小平方估计可表示为：
$$\hat{x}(y)=y+{\sigma }^2{\nabla }_{y}logp(y)\text{\hspace{1em}(2)}$$
公式(2)可有简单的推导获得，观测密度(公式1)的梯度可以表示为：
$$\begin{array}{rl}{\nabla }_{y}p(y)& =\frac{1}{{\sigma }^2}\int (x-y)g(y-x)p(x)dx\\ & =\frac{1}{{\sigma }^2}\int (x-y)p(x,y)dx\end{array}\text{\hspace{1em}(3)}$$
两篇同时乘上${\sigma }^2/p(y)$可以得到：
$$\begin{array}{rl}{\sigma }^2\frac{{\nabla }_{y}p(y)}{p(y)}& =\int xp(x|y)dx-\int yp(x|y)dx\\ & =\hat{x}(y)-y\end{array}\text{\hspace{1em}(4)}$$
这里我们利用$log$来计算梯度。直观上看，公式(2)说明了去噪器使用梯度上升的方法，通过上移概率梯度从观测信号中去除噪声。因此，假设我们希望从去噪器中的先验隐式中抽取样本，公式(4)允许我们通过计算降噪残差$f(y)=\hat{x}(y)-y$来生成与$logp(y)$的梯度成正比的图像。Score-based mode是在马尔科夫链中发展了与本文的相关计算，结合了分数匹配的梯度步骤和加噪的Langevin采样方法从密度序列$p_{\sigma }(y)$中进行采样，在以离散去噪的同时，每一步中都会关联一个适当训练的去噪器。 本文从一个随机初始化$y_0$开始，目标是使用更简单且高效的随机梯度上升过程找到一个高概率图像。本文采用一个能够处理不同噪声强度的bias-free的CNN去噪器的残差$f(y)$来计算梯度，每次迭代过程都在梯度的方向上采取确定的步骤，并注入一些额外的噪声：
$$y_t=y_{t-1}+h_{t}f(y_{t-1})+{\gamma }_t{z}_t\text{\hspace{1em}(5)}$$
我们可以看到这与Langevin动力学采样算法几乎一致，其中$h_t\in [0,1]$控制着去噪矫正比，而${\gamma }_t$控制着噪声的振幅，目的避免陷入局部最大值，这个想法与Socre也很相似。我们可以知道第$t$步$y_t$的有效噪声方差为：
$${\sigma }_t^2=(1-h_t{)}^2{\sigma }_{t-1}^2+{\gamma }_t^2$$
其中第一项是经过了去噪器矫正后的剩余噪声方差，第二项是额外注入的噪声方差。这里我们假设去噪器可以能够有效的降低$(1-h_t)$的标准差，为了达到收敛，尽管添加了额外的噪声，我们需要每次迭代步数有效的减少方差。因此引入了参数$\beta \in [0,1]$来控制加入噪声的比例（当$\beta =1$时额外加的噪声为0），通过下面的公式来强制网络收敛：
$${\sigma }_t^2=(1-\beta h_t{)}^2{\sigma }_{t-1}^2=(1-h_t{)}^2{\sigma }_{t-1}^2+{\gamma }_t^2$$
我们可以获得${\gamma }_t$的表达式：
$$\begin{array}{rl}{\gamma }_t^2& =[(1-\beta h_t{)}^2-(1-h_t{)}^2]{\sigma }_{t-1}^2\\ & =[(1-\beta h_t{)}^2-(1-h_t{)}^2]||f(y_{t-1})|{|}^2/N\end{array}$$
其中$N$代表像素值的数量，第二行假设去噪残差的大小能够提供标准差的良好估计。这能够允许去噪器自适应的控制梯度上升的步长，在$y_t$接近目标分布时可以自动调整减少步长。$h_t$参数的设定为$h_t=h_{0}t/1+h_0(t-1),h_0\in [0,1]$。采样算法如下：

4. 图像生成案例

图像生成的案例，去噪器选择BF-CNN，参数${\sigma }_0=1,{\sigma }_L=0.01,h_0=0.01$。如图1，$\beta =1$既没有额外的噪声添加，算法会放大并”halluciantes“噪声中发现的结构，此外没有随机噪声的情况下，算法在少于40次迭代收敛。图2左边为$\beta =0.5$，中等水平的噪声注入，可以看到图片包含了自然的特征，具有锐利的轮廓，阴影和细致的纹理区域等。图2右边是更大的噪声注入$\beta =0.1$，额外的噪声有助于避免局部最大值，获得的图像质量也可以，但是延长了收敛时间。

5. 用隐式先验解决逆问题

信号处理中的许多应用都可以用确定的线性逆问题来表达，如去模糊，超分，估计缺失像素和压缩感知等。给定一个线性测量(linear measurements)的图像集合，$x^c=M^{T}x$，这里$M$是一个低秩测量矩阵，我们尝试恢复原始图像。上面提出了一种随机梯度上升的算法用于从$p(x)$中采样，这里我们以条件密度$p(x|M^{T}x=x^c)$求解逆问题。

5.1 有约束的采样算法

考虑噪声图像$y$的分布以线性观测$x^c=M^{T}x$为条件，不失一般性，我们假设矩阵$M$的列是正交单位向量（如果不是，我们可以使用SVD重参化为等效约束，后面的文章要用！）：
$$p(y|x^c)=p(y^c,y^u|x^c)=p(y^u|x^c,y^c)p(y^c|x^c)=p(y^u|x^c)p(y^c|x^c)$$
注：$P(B,C|A)=P(C|A,B)P(B|A)$，其中$y^c=M^{T}y,y^u={\bar{M}}^{T}y$（$y$在$M$正交补集的投影）。公式2中的梯度就可以改写为：
$${\sigma }^2{\nabla }_{y}logp(y|x^c)={\sigma }^2{\nabla }_{y}logp(y^u|x^c)+{\sigma }^2{\nabla }_{y}logp(y^c|x^c)\text{\hspace{1em}(6)}$$
这里的第二项是投影到测量空间的观测噪声的梯度。如果高斯噪声的方差是${\sigma }^2$，则在观测空间噪声减小的值为$M(y^c-x^c)$，记住梯度是与$f(y)$成正比的。第一项是仅在与测量正交的子空间内定义的函数的梯度，因此可以通过将测量子空间投影到整个梯度之外来计算。注意，$M$是$M^T$的伪逆，且矩阵$M{M}^T$可以用于将图像投影到测量子空间。根据分析，公式6可以等价于：
$$\begin{array}{rl}{\sigma }^2{\nabla }_{y}logp(y)& =(I-M{M}^T){\sigma }^2{\nabla }_{y}logp(y)+M(x^c-y^c)\\ & =(I-M{M}^T)f(y)+M(x^c-M^{T}y)\end{array}$$
因此，我们可以看到条件密度的梯度被分为两个正交的成分，分别是捕获噪声密度和有约束的偏差。这里同样使用上面的算法：

6. 线性逆问题案例

本文展示了该方法应用在几个线性逆问题的结果，每个案例都使用相同的算法和参数，只有测量矩阵$M$和测量值$M^{T}x$发生变化。去噪器选择BF-CNN，参数${\sigma }_0=1,{\sigma }_L=0.01,h_0=0.01,\beta =0.01$。

6.1 Inpainting

线性逆问题的一个简单示例包含恢复缺失像素块，且以周围的内容为条件。因此该任务中的测量矩阵的列是一个单位矩阵的子集，对应测量（外部）像素位置。（代码有待更新）

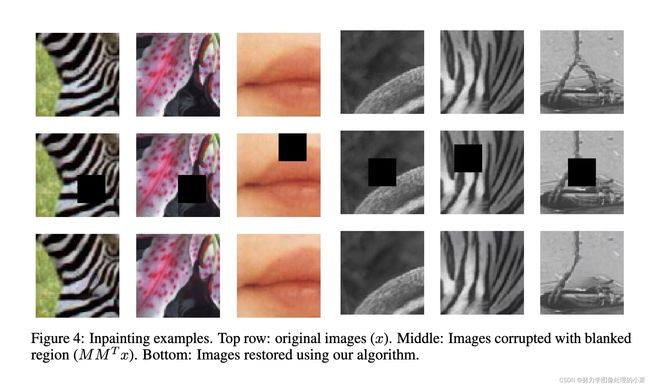
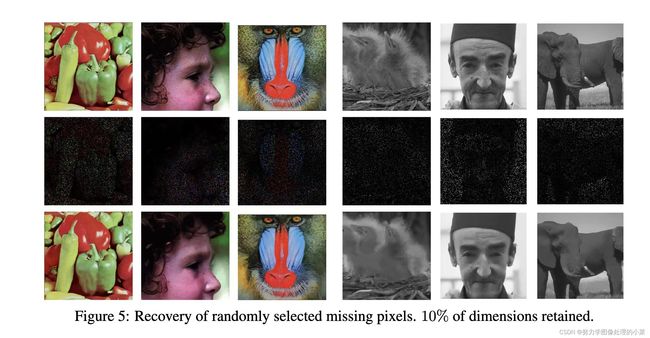
6.2 Random missing pixels

考虑到随机丢弃像素子集的测量过程，$M$是一个低秩矩阵，其列是单位矩阵的子集，对应着随机选择保留的像素集合。图5展示了90%的像素丢弃，仅仅保留图像中10%的像素，说实话我觉得恢复的效果非常好，但是psnr不一定会高。

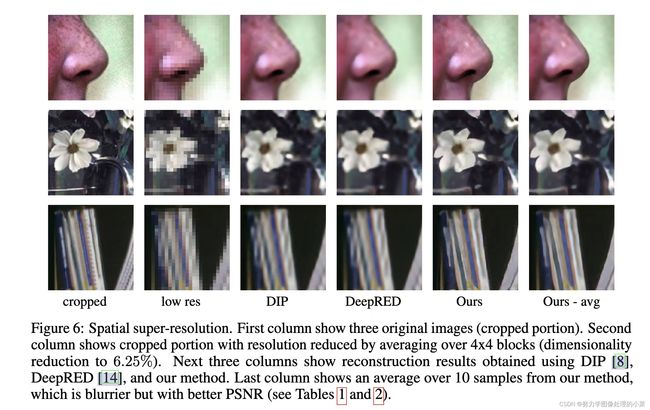
6.3 Super-resolution

超分中的下采样操作通常在低通滤波后执行，下采样因子和滤波核的组合决定了测量模型$M$，本文采用$4\times 4$均值滤波和$4\times 4$下采样。本文对比了Deep image Prior (DIP)链接，Deep Image Prior Powered by RED (DeepRED)链接。

6.4 Deblurring (Spectral super-resolution)

本文考虑的模糊算子是在傅里叶域中保留一组低频系数然后丢弃其余部分来获得空域的模糊图像。$M$是离散傅里叶变换的保留低频列组成。

6.5 Compressive sensing

不是很熟悉这里，以后来填坑。

总结

本文提出了一个框架，用嵌入在去噪器中的先验知识来解决逆问题。文章仅仅举例了一些“乘性降质”的案例，图像去噪也是一个重要的逆问题，本文没有给出如何解决的方法 (后面的跟进研究解决了这个问题链接)。此外，本文构建了分数函数(score function)与 MMSE 降噪器之间的极有价值的联系，本文与扩散模型的思想非常相似，区别在于本文没有前向的扩散过程，并使用的是一个预训练去噪器。（我认为该算法的性能和去噪器的性能也应该是正比的关系。）而且本文解决逆问题也是一定程度上依赖于hand-crafted，在处理真实任务上的方面有待进一步研究。总之，本文给出了一个非常漂亮的算法推导和思想，这对应用扩散模型在low-level任务上提供了更多的基础理论和insights。