数字图像处理 第二章数字图像基础

第二章 数字图像基础

本章全都不是重点，了解就好

目标

人体视觉感知

光和电磁波谱

成像模型

图像取样与量化

一些基本概念和数学处理方法

人体视觉感知

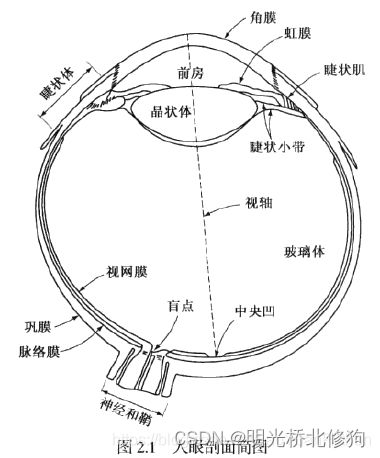
人眼结构

上图为人眼剖面图。

人眼是一个直径约为20mm的球体，从外到内由三层膜包裹，分别是角膜，巩膜共同组成第一层，脉络膜，视网膜。

• 角膜

  角膜坚硬且透明，覆盖人眼前表面

• 巩膜

  巩膜不透明，包裹角膜未包裹到的地方

• 脉络膜位于巩膜正下方，含有大量血管，供给眼球营养。脉络膜颜色很深，可以减少入射光线和反向散射的光线，脉络膜前端分为睫状体和虹膜，虹膜开口的直径可变，控制入射光的量

• 晶状体

  由同心纤维细胞构成，悬挂在睫状体上，由睫状体牵引，所以可以改变厚度，控制焦距。晶状体含有黄色素，当黄色素增多，就是白内障。晶状体到视网膜的距离大约17mm，这个数字不会变。

• 视网膜

  眼球中最内部的是视网膜，它布满整个眼球后壁。成像也是发生在这里。感受器分为视锥细胞(cone cell)和视杆细胞(rod cell)。

  也有叫锥状体和杆状体的，差不多。

  其中，视锥细胞有大约600~700万个，集中在中央凹处，每个细胞连接一个神经末梢，视杆细胞有7500~15000万个，多个细胞连接一个神经元，所以感知细节的能力比视锥细胞弱。视锥细胞对颜色高度敏感，而视杆细胞没有色觉，对低光照度敏感，也就是说能在光纤弱的地方识别物体的大概轮廓，缺没有颜色。可以这样理解，视锥细胞对颜色、细节敏感，但是对光强不敏感；视杆细胞对颜色不敏感，对光强尤其是光纤较少时敏感。所以视锥细胞产生的视觉也叫明视觉，视杆细胞产生的视觉也叫暗视觉。

• 中央凹

  直径$1.5mm$的圆形凹陷，面积约$1.77m{m}^2$。视锥细胞大部分分布于此，而视杆细胞在此区域没有分布。电子成像芯片的传感器比人眼的感受器密度高多了，但是目前感知能力还不能超越人。cuz human brain is complicated

人眼成像

视锥细胞和视杆细胞获取信息经过大脑神经网络形成视觉。

照相机调焦是改变透镜和感光胶片之间的距离，而人眼与此相反：人眼通过调节晶状体的厚度来调焦。

人类成像感知错觉

举个栗子，自己看吧

马赫带：

马赫带亮度图解：

光和电磁波谱

电磁波可以看作以波长$\lambda$，频率$\nu$传播的正弦波

波长和频率的关系：
$$\lambda =c/\nu$$
$c$为光速

能量和频率的关系：
$$E=h\nu$$
$h$为普朗克常量，可以看出能量和频率成正比，因此更高频的电磁波携带能量越多，可见光的波长从$0.43\mu m\sim 0.79\mu m$，从高到低分别为红橙黄绿蓝靛紫。

没有颜色的光称为单色光，其唯一属性为其亮度，从黑色到灰色，再到白色。所以这种单色光形成的图像也称为灰度图像(grayscale image)。

成像模型

用形如$f(x,y)$的二维函数表示图像，在空间坐标$(x,y)$处的$f$的值是一个标量，与电磁波辐射能量成正比，所以$f(x,y)$一定是非负且有限的。但是在图像处理过程中可能会出现负值，一般的做法是在0处截断。

$f(x,y)$由两个分量表征，分别是入射光的光强，和物体反射率，分别称为入射分量i(x,y)，反射分量r(x,y)。
$$f(x,y)=i(x,y)r(x,y)$$
令空间坐标$(x,y)$处的亮度（灰度)为
$$l=f(x,y)$$
有式$i_{min}{r}_{min}⩽l⩽i_{max}{r}_{max}$

用$L$表示亮度，那么$L_{min}⩽l⩽L_{max}$

$[L_{min},L_{max}]$表示亮度级（灰度级）

图像取样与量化

采样与量化涉及《通信原理》和《信号与系统》，这里简单介绍。

如真实世界中的一样，传感器感测到的图像数据的灰度是连续变化的，遗憾的是计算机是数字的，需要将图像也转化为数字的。

对坐标进行数字化叫做采样，对幅度进行数字化叫做量化。图像中用到的就是最简单的均匀量化，即跨越相同的灰度给定一个灰度值。

拉一条线横跨图像，宽度为一个像素，从上向下扫描整个图像依次完成量化最终得到一幅像素图。

数字图像表示

数字图像$f(x,y)$，$x,y,f$的值都是整数，图像坐标张成的实平面称为空间域。

一般的，用一个矩阵表示图像，假设图像$M$行$N$列：
f ( x , y ) = [ f ( 0 , 0 ) f ( 0 , 1 ) ⋯ f ( 0 , N − 1 ) f ( 1 , 0 ) f ( 1 , 1 ) ⋯ f ( 1 , N − 1 ) ⋮ ⋮ ⋱ ⋮ f ( M − 1 , 0 ) f ( M − 1 , 1 ) ⋯ f ( M − 1 , N − 1 ) ] f(x,y)= \begin{bmatrix} f(0,0) & f(0,1) & \cdots & f(0,N-1)\\ f(1,0) & f(1,1) & \cdots & f(1,N-1)\\ \vdots & \vdots & \ddots & \vdots\\ f(M-1,0) & f(M-1,1) &\cdots & f(M-1,N-1) \end{bmatrix} f(x,y)= ​f(0,0)f(1,0)⋮f(M−1,0)​f(0,1)f(1,1)⋮f(M−1,1)​⋯⋯⋱⋯​f(0,N−1)f(1,N−1)⋮f(M−1,N−1)​ ​
MATLAB索引从1开始

坐标系中x轴竖直向下，y轴水平向右。因为大多数显示器，例如电视，都是从左上角开始一行一行的扫描，这与矩阵的编号也相同，所以有时候也用行$r$，列$c$来替换$x,y$。

图像的中心在$(x_c,y_c)=(round(M/2),round(N/2))$，有时也可以用向下取整$(x_c,y_c)=(\lfloor M/2\rfloor ,\lfloor N/2\rfloor )$。

图像数字化中的一些重要概念

• 灰度级

  用$L$表示：$L=2^k$，2懂得都懂，依赖于存储和量化硬件，$k$通常是一个像素的比特数，通常是8的倍数。

• 动态范围

  本书将系统中最大可度量灰度与最小可度量灰度的比值称为动态范围，描述灰度跨越的值域。

• 对比度

  一幅图像中最高和最低灰度级之间的灰度差

• 反差比

  前两者的比值，了解一下，后面会详细分析

存储一幅数字图像所需的比特数为
$$b=MNk$$
一幅图像具有$2^k$个可能的灰度级时，称该图像为k比特图像，如一幅256级图像称一幅8比特图像。

空间分辨率和灰度分辨率

• 空间分辨率

  空间分辨率指图像中最小可分辨细节的测度，经典的是单位距离中的线对数和单位距离的点数（像素数）。

  线对数：一条线宽$W$，一条黑线一条白线交替排列，一条黑线和一条白线组成一个线对，不同的图像线宽不同。那么，单位距离内线对数就可以描述空间分辨率，同样单位距离内像素数也可以描述空间分辨率。比如单位dpi(dot per inch，一英寸$=2.54cm$)就是空间分辨率的一个单位。空间分辨率只有针对单位空间距离时才有意义，比如两台相机分别装备20兆像素的成像芯片和8兆像素的成像芯片，只有在相同距离拍照，拍出来的照片才能说20兆像素的相机牛批。

• 灰度分辨率

  同样，灰度分辨率指在灰度级中可分辨的最小变化。通常指量化灰度时所用的比特数。但是灰度可分辨率受噪声和饱和度影响，还受人类分析和解释整个场景内容的感知能力影响。

一些基本概念和数学处理方法

一些数学背景和处理介绍

图像内插

图像内插，就是插值的一个方法，主要用在图像缩放，旋转和几何校正。内插法，也叫插值法，是用已知数据来估计未知位置的值的过程。

• 最近邻内插

  假设一幅大小$500\times 500$像素的图像，现在想将其放大1.5倍，也就是放大到$750\times 750$像素。

  先创建一个$750\times 750$像素的假象网格，像素间隔和原来的图像相同，收缩假象网格，让其适应原来$500\times 500$的网格，现在像素间隔缩小，找到原图中与每个缩小后的像素最临近的像素，将其像素值赋予假象网格。这就是最近邻内插。

• 线性内插
  

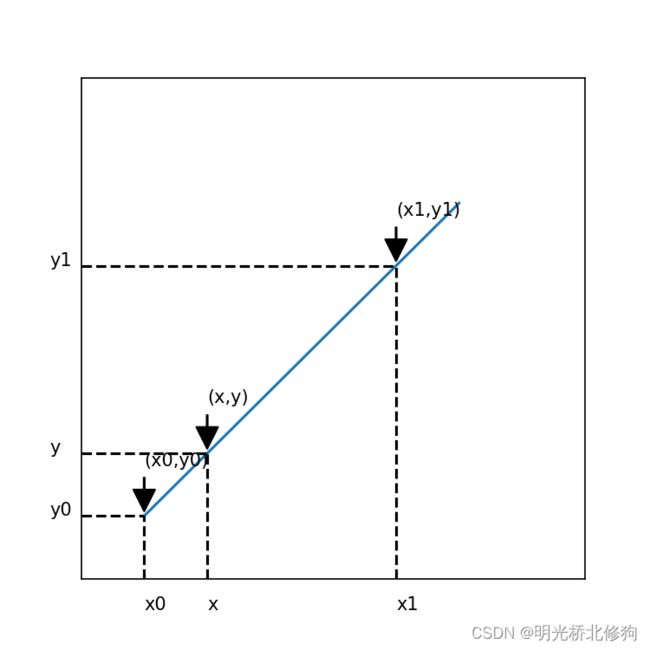
  已知$(x,y)$在某一直线上，直线上$(x0,y0),(x1,y1)$已知，且已知$x$的值。求y的值，插入的值就是$y$。

  很简单，根据三角形相似，有：
  $$\frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0}$$
  设$x$轴上的比例为：
  $$\alpha =\frac{x-x_0}{x_1-x_0}$$
  结合两式：
  $$y=(1-\alpha )y_0+\alpha y_1$$

• 二次线性内插

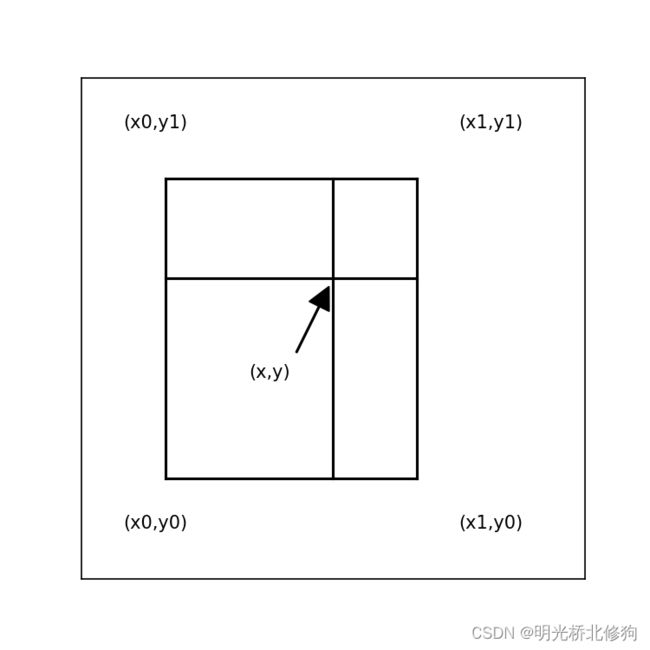
  虽然名为二次线性内插，也叫双线性内插，但这并不是一个线性运算，而是使用了三次线性内插。描述数字图像$f=(x,y)$应该使用三维空间，设$z$轴表示灰度值，$(x,y)$描述空间位置，$(x,y)$的四个最近邻分别为$(x0,y0),(x0,y1),(x1,y0),(x1,y1)$，其中$y1-y0=x1-x0=1$。那么首先在y方向上做两次线性内插得到两个值，再在x方向上用这两个值做一次线性内插就可以得到$(x,y)$处的$z$值。

步骤如下：
$$\begin{gathered} f(x0,y0)=(1-\alpha )f(x0,y0)+\alpha (x1,y0) \\ f(x0,y1)=(1-\alpha )f(x0,y1)+\alpha (x1,y1) \\ f(x,y)=(1-\beta )f(x,y0)+\beta f(x0,y1) \\ f(x,y)=(1-\alpha )(1-\beta )f(x0,y0)+\alpha (1-\beta )f(x1,y0)+\beta (1-\alpha )f(x0,y1)+\alpha \beta f(x1,y1) \end{gathered}$$
其中坐标$(x0,y0),(x0,y1),(x1,y0),(x1,y1)$分别为假象网格收缩后在原图中最邻近的四个像素。

• 双三次内插

  hh，这个我真不会

最近邻内插图像失真有时会比较严重，一般用双线性内插，复杂度不高，失真也是会有，OpenCV默认内插算法。

像素间的一些基本关系

某个特定像素用小写字母表示，如$p,q$

像素的相邻像素

坐标$(x,y)$处的像素$p$有2个水平的相邻像素和2个垂直相邻的像素，坐标为
$$(x+1,y),(x-1,y),(x,y+1),(x,y-1)$$
这组像素称为$p$的4邻域，用$N_4(p)$表示。

$p$的四个对角线像素坐标为
$$(x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)$$
这组像素用$N_D(p)$表示。

$N_4(p)$和$N_D(p)$和起来称为$p$的8邻域，用$N_8(p)$表示。

邻接，连通，区域和边界

利用集合论中的知识。令$V$是定义邻接灰度值的集合。

那么，在一幅二值图像（二值图像指像素值只有两个的黑白图像）中。值为1的像素邻接指的是$V=\{1\}$。其他图像也是类似的，比如8比特图像$V$可能是256个值的子集。

邻接类型：

1. 4邻接。$q$在集合$N_4(p)$中时，值在$V$中的两个像素$p,q$是4邻接的。
2. 8邻接。$q$在集合$N_8(p)$中时，值在$V$中的两个像素$p,q$是8邻接的。
3. m邻接（混合邻接）。如果
   • $q$在$N_4(p)$中，或者
   • $q$在$N_D(p)$中，且集合$N_4(p)\cap N_4(q)$中没有在$V$中的像素

混合邻接是8邻接的改进，为了消除8邻接的歧义：
[ 0 1 1 0 1 0 0 0 1 ] \begin{bmatrix} 0 & \textcolor{blue}1 & \textcolor{blue}1\\ 0 & \textcolor{blue}1 & 0\\ 0 & 0 & \textcolor{blue}1 \end{bmatrix} ​000​110​101​ ​
如果使用8邻接，那么上面的矩阵的上两行的1两两都是8邻接的。但是如果使用m邻接，那么第一行最后一个1和第二行的1不是m邻接的。

数字通路

从坐标为$(x_0,y_0)$的像素$p$到坐标$(x_n,y_n)$的像素$q$的数字通路是不同像素序列，像素坐标为
$$(x_0,y_0),(x_1,y_1),\cdots ,(x_n,y_n)$$
式中$(x_i,y_i)$和$(x_{i-1},y_{i-1})$在$1⩽i⩽n$时是邻接的。$n$是通路长度。$(x_0,y_0)=(x_n,y_n)$时通路是闭合通路。根据邻接不同类型的定义，可以将通路也定义为4邻接、8邻接和m邻接。

令$S$为图像中像素的一个子集。对于S中任何像素$p$，在$S$中连通到该像素的像素集称为$S$的连通分量，若$S$中仅有一个连通分量，则称$S$为连通集。这里和图论中的差不多。

令$R$表示图像中像素的一个子集。若$R$是一个连通集，则称$R$为图像的一个区域。两个区域$R_i,R_j$联合形成一个连通集时，称$R_i,R_j$为邻接区域。不邻接的区域称为不相交区域。区域的定义中不考虑混合邻接，只有4邻接和8邻接。

前景，背景

设一幅图像中含有$K$个不相交的区域$R_k,k=1,2,\cdots ,K$，并且他们与图像的边界不相连。令$R_u$表示所有$K$个区域的并集，令$(R_u{)}^c$表示其补集，称$R_u$中所有点为图像的前景，称$(R_u{)}^c$中所有点为图像背景。

边界（边框or轮廓）

区域$R$的边界是$R$与$R$的补集中的像素响相邻的一组像素。也就是说一个区域的边界是该区域中至少有一个背景邻接点的像素集。

谈到像素邻接点，就必须指出是哪种类型的邻接，如：
[ 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 ] \begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 0 & \textcolor{blue}1 & \textcolor{blue}1 & 0 & 0\\ 0 & \textcolor{blue}1 & \textcolor{blue}1 & 0 & 0\\ 0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}1 & 0\\ 0 & \textcolor{blue}1 & \textcolor{blue}1 & \textcolor{blue}1 & 0\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} ​000000​011110​011110​000110​000000​ ​
中第四行第三列的1，如果使用4连通，那么该1不是边界成员，如果使用8连通，则是边界成员。

以上的定义是内边界，外边界则是背景中对应的。

注意：边界和后面出现的边缘是两个东西

距离测度

定义：

对于坐标分别为$(x,y),(u,v),(w,z)$的像素$p,q,s$，如果

• $D(p,q)⩾0[D(p,q)=0当且仅当p=q]$
• $D(p,q)=D(q,p)$
• $D(p,s)⩽D(p,q)+D(q,s)$

则$D$是一个距离函数或者距离测度。

欧几里得距离
$$D_e(p,q)=[(x-u{)}^2+(y-v{)}^2{]}^{\frac{1}{2}}$$
$D_4$距离（城市街区距离）
$$D_4(p,q)=|x-u|+|y-v|$$
轮廓如下：
[ 2 2 1 2 2 1 0 1 2 2 1 2 2 ] \begin{bmatrix} & & 2 & &\\ & 2 & 1 & 2 &\\ 2 & 1 & 0 & 1 & 2\\ & 2 & 1 & 2 &\\ & & 2 & &\\ \end{bmatrix} ​2​212​21012​212​2​ ​
其中$D_4=1$的像素是$(x,y)$的四邻域。

$D_8$距离（棋盘距离）
$$D_8(p,q)=max(|x-u|,|y-v|)$$
轮廓如下：
[ 2 2 2 2 2 2 1 1 1 2 2 1 0 1 2 2 1 1 1 2 2 2 2 2 2 ] \begin{bmatrix} 2 & 2 & 2 & 2 & 2\\ 2 & 1 & 1 & 1 & 2\\ 2 & 1 & 0 & 1 & 2\\ 2 & 1 & 1 & 1 & 2\\ 2 & 2 & 2 & 2 & 2\\ \end{bmatrix} ​22222​21112​21012​21112​22222​ ​
其中$D_8=1$的像素是$(x,y)$处像素的8邻域。

举个栗子：
[ p 3 p 4 p 1 p 2 p ] \begin{bmatrix} & p_3 & p_4\\ p_1 & p_2 & \\ p \end{bmatrix} ​p1​p​p3​p2​​p4​​ ​
其中$p,p_2,p_4$为1，$p_1,p_3$为0或1。

考虑$V=\{1\}$

若$p_1,p_3=0$，则$p,p_4$之间最短的m通路距离为2。

若$p_1=1,p_3=0$或者$p_1=0,p_3=1$，则$p,p_4$之间最短的m通路距离为3。

若$p_1=1,p_3=1$，则$p,p_4$之间最短的m通路距离为4。

一些关于图像的数学运算

原书中的一些很基础的运算略。

空间运算

1. 单像素运算

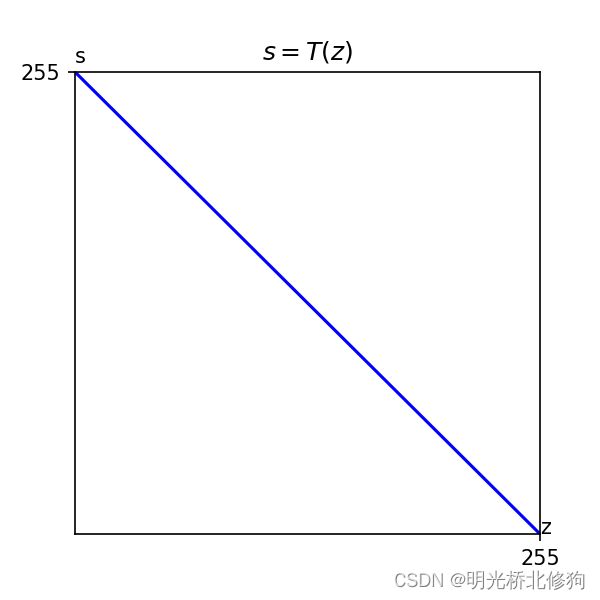
   用一个变换函数$T$改变图像中的各个像素的灰度
   $$s=T(z)$$
   $z$是原图中的像素的灰度，$s$是处理后图像的像素的灰度。

   比如想要得到一幅8比特图像的负图像（负片的数字图像，并不是简单取负值）：

   

邻域运算

令$S_{xy}$代表图像$f$中以任意一点$(x,y)$为中心的一个邻域的坐标集。邻域运算就是利用输入图像中的而邻域的像素值做规定运算确定$(x,y)$处的像素值的运算。如，规定运算是计算大小$m\times n$，中心为$(x,y)$的矩形邻域中的像素的平均值。这个区域像素坐标集合是$S_{xy}$。

这一平均运算表示为：
$$g(x,y)=\frac{1}{mn}\sum _{(r,c)\in S_{xy}}f(r,c)whererandcarerowsandcolumns$$

几何变换

用的多的是仿射变换，包括以下步骤：

1. 坐标的空间变换
2. 灰度内插，即变换后有一些地方需要赋值，利用内插法插值

可表示为
$$\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\end{array}\right]=\mathbf{T}\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
其中$(x,y)$是原图中像素的坐标，$(x^{{}^{\prime }},y^{{}^{\prime }})$是变换后图像中像素的坐标。比如变换$(x^{{}^{\prime }},y^{{}^{\prime }})=(x/2,y/2)$是在两个方向上将原图缩小一半。

仿射变换包括缩放，平移，旋转和剪切。

平移变换需要给矩阵增加一个维度：
[ x ′ y ′ 1 ] = A [ x y 1 ] = [ a 11 a 12 a 13 a 21 a 22 a 23 0 0 1 ] [ x y 1 ] \begin{bmatrix} x^{'}\\ y^{'}\\ 1 \end{bmatrix}=\mathbf{A}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}= \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ​x′y′1​ ​=A ​xy1​ ​= ​a11​a21​0​a12​a22​0​a13​a23​1​ ​ ​xy1​ ​
除此之外，还要给新位置进行插值。

变换名	仿射矩阵A	坐标公式
恒等	[ 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix}1 &0 & 0\\ 0 & 1 & 0\\0 & 0 & 1\end{bmatrix} ​100​010​001​ ​	$$\begin{gathered} x^{{}^{\prime }}=x \\ {y}^{{}^{\prime }}=y \end{gathered}$$
缩放	[ c x 0 0 0 c y 0 0 0 1 ] \begin{bmatrix}c_x & 0 & 0\\0 & c_y & 0\\0 & 0 & 1\end{bmatrix} ​cx​00​0cy​0​001​ ​	$$\begin{gathered} x^{{}^{\prime }}=c_{x}x \\ {y}^{{}^{\prime }}=c_{y}y \end{gathered}$$
旋转	[ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] \begin{bmatrix}cos\theta & -sin\theta & 0\\sin\theta & cos\theta & 0\\0 & 0 & 1\end{bmatrix} ​cosθsinθ0​−sinθcosθ0​001​ ​	$$\begin{gathered} x^{{}^{\prime }}=xcos\theta -ysin\theta \\ {y}^{{}^{\prime }}=xsin\theta +ycos\theta \end{gathered}$$
（垂直）剪切	[ 1 s v 0 0 1 0 0 0 1 ] \begin{bmatrix}1 &s_v &0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix} ​100​sv​10​001​ ​	$$\begin{gathered} x^{{}^{\prime }}=x+s_{v}y \\ {y}^{{}^{\prime }}=y \end{gathered}$$
（水平）剪切	[ 1 0 0 s h 1 0 0 0 1 ] \begin{bmatrix}1 & 0 & 0\\s_h & 1 & 0\\0 & 0 & 1\end{bmatrix} ​1sh​0​010​001​ ​	$$\begin{gathered} x^{{}^{\prime }}=x \\ {y}^{{}^{\prime }}=s_{h}x+y \end{gathered}$$

反变换：
$$(x,y)=A^{-1}(x^{{}^{\prime }},y^{{}^{\prime }})$$

图像变换

以上的处理都是直接对像素进行操作，即工作在空间域。

而有些情况，图像处理最好按照以下步骤进行：

• 变换输入图像
• 在变换域进行规定任务
• 反变换回空间域

二维线性变换是一种特别重要的变换。假设$T(u,v)$为一种二维线性变换：
$$T(u,v)=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}T(u,v)r(x,y,u,v)$$
$f(x,y)$为输入图像，$r(x,y,u,v)$为正变换核，$T(u,v)$为$f(x,y)$的正变换。

对应反变换：
$$f(x,y)=\sum _{u=0}^{M-1}\sum _{v=0}^{N-1}T(u,v)s(x,y,u,v)$$
$s(x,y,u,v)$为反变换核。

上面两式一起叫做变换对。

线性变换中的一般操作：

T(u,v)

R[T(u,v)]

f(x,y)

变换

运算R

反变换

g(x,y)

其中$f,g$在空间域，里面三个在变换域中。

如果
$$r(x,y,u,v)=r_1(x,u)r_2(y,v)$$
则可以说正变换核是可分离的。

如果$r_1(x,u)$的作用等同于$r_2(y,v)$那么称变换是对称的。

典中典之傅里叶变换（Fourier Transform）：
$$\begin{gathered} r(x,y,u,v)=e^{-j2\pi (ux/M+vy/N)} \\ s(x,y,u,v)=\frac{1}{MN}{e}^{j2\pi (ux/M+vy/N)} \end{gathered}$$
后面再讨论，先给傅里叶磕个头。

图像灰度核随机变量

令$z_i,i=0,1,2,\cdots ,L-1$为一幅$M\times N$数字图像的所有可能灰度值。灰度级$z_k$在此图中出现的概率$p(z_k)$为
$$p(z_k)=\frac{n_k}{MN}$$
$n_k$为$z_k$在图像中出现的次数，$MN$为像素总数。明显有
$$\sum _{k=0}^{L-1}{z}_{k}p(z_k)=1$$
平均灰度为
$$m=\sum _{k=0}^{L-1}{z}_{k}p(z_k)$$
灰度的方差为
$${\sigma }^2=\sum _{k=0}^{L-1}(z_k-m{)}^{2}p(z_k)$$