滤波学习理解----EKF(二)
多个观测源+目标状态值维度为n的向量+观测值维度为m1,m2的向量
滤波模型依旧是如下抽象模型,因为是matrixXd所以可以根据数据源维度进行Z,H,R的维度切换。
预测模型:
x i ′ = F ∗ x i − 1 x'_{i}=F*x_{i-1} xi′=F∗xi−1
P i ′ = F ∗ P i − 1 ∗ F T + Q P'_{i}=F*P_{i-1}*F^{T}+Q Pi′=F∗Pi−1∗FT+Q
更新模型:
y = z − H ∗ x i ′ y=z-H*x'_{i} y=z−H∗xi′
K = P i ′ ∗ H T ∗ ( H ∗ P i ′ ∗ H T + R K=P'_{i}*H^{T}*(H*P'_{i}*H^{T}+R K=Pi′∗HT∗(H∗Pi′∗HT+R
x i = x i ′ + K ∗ y x_{i}=x'_{i}+K*y xi=xi′+K∗y
P i = ( I − K ∗ H ) ∗ P i ′ P_{i}=(I-K*H)*P'_{i} Pi=(I−K∗H)∗Pi′
所以上面的kf2.h和kf2.cpp在本案例中也是需要的,就不重复粘贴了。但是直接使用显然会遇到一些问题。所以针对多信息源融合我们需要单独写一个融合ekf_fusion的类。
代码原型如下:
ekf_fusion2.h
#include "kf2.h"
struct MeasurementPackage
{
long long timestamp;//每个数据的时间戳都需要记录,主要是数学模型中需要deltaT
enum Sensor_Type{
RADAR,
VISUAL
} sensorType;//是有枚举区分不同数据源,不同数据源的Z,H和R的维度&数值是不同的
Eigen::VectorXd raw_measurements;//观测数据
};
class ekf_fusion2
{
public:
ekf_fusion2(){init();}
~ekf_fusion2(){}
void init();//初始化数据维度&数值
void ProcessMeasurement(const MeasurementPackage &measurement_pack);//进行EKF滤波融合的核心步骤
Eigen::VectorXd getX(){return ekf_.X_;}//获得返回值
private:
kalman_filter ekf_;//卡尔曼滤波通用模块,参考kf2.h和kf2.cpp
bool is_initialized;//数据跟踪的时候需要有个初始化的步骤,由于有多个数据源,不同数据源的初始化的步骤不同。
long long previous_timestamp;//记录上一次观测数据输入的时间戳,方便计算deltaT
double noise_ax,noise_ay,noise_aw;//噪声参数
Eigen::MatrixXd R_radar;
Eigen::MatrixXd R_visual;
Eigen::MatrixXd H_radar;
Eigen::MatrixXd H_visual;
MatrixXd CalculateJacobian(const VectorXd& x_state);//计算雅可比矩阵
};
多个观测源所有多个观测噪声R和多个转换矩阵H。除此之外,不同观测噪声进行初始化同样需要区分,所以需要单独的is_initialized的初始化标志布尔值。由于数学模型中存在deltaT的关系,所以在数据源MeasurementPackage中也需要携带deltaT。
ekf_fusion2.cpp
#include "ekf_fusion2.h"
void ekf_fusion2::init()
{
is_initialized=false;
previous_timestamp = 0;
R_radar = MatrixXd(3, 3);//观测噪声协方差矩阵:radar
R_radar =Eigen::Vector3d(0.09,0.009,0.09).asDiagonal();
R_visual = MatrixXd(2, 2);//观测噪声协方差矩阵:visual
R_visual = Eigen::Vector2d(0.0225,0.0225).asDiagonal();
H_radar = MatrixXd(3, 4);//变换矩阵H :radar
H_visual = MatrixXd(2, 4);//变换矩阵H :visual
H_visual << 1, 0, 0, 0,
0, 1, 0, 0;
ekf_.F_ = MatrixXd(4,4);//设置数学模型矩阵F的维度
ekf_.Q_ = MatrixXd(4,4);//设置系统噪声协方差矩阵Q的维度
ekf_.P_ = MatrixXd(4, 4); //状态协方差矩阵P
ekf_.P_ = Eigen::Vector4d(1,1,1000,1000).asDiagonal();
noise_ax=0.05;//噪声
noise_ay=0.05;
}
void ekf_fusion2::ProcessMeasurement(const MeasurementPackage &measurement_pack)
{
/*******初始化**********
TODO:
* 根据第一个数据的类型,初始化ekf_.x_
* 需要将radar的坐标系从极坐标系转化为平面坐标系
*******************************/
if (!is_initialized) {
ekf_.x_ = VectorXd(4);
if (measurement_pack.sensorType == MeasurementPackage::RADAR) {
// Initialize radar state.
float rho = measurement_pack.raw_measurements_[0];
float phi = measurement_pack.raw_measurements_[1];
float rho_dot = measurement_pack.raw_measurements_[2];
float position_x = rho * cos(phi);
if (position_x < 0.0001) {
position_x = 0.0001;
}
float position_y = rho * sin(phi);
if (position_y < 0.0001) {
position_y = 0.0001;
}
float velocity_x = rho_dot * cos(phi);
float velocity_y = rho_dot * sin(phi);
ekf_.x_ << position_x, position_y, velocity_x , velocity_y;
} else {
// Initialize visual state.
ekf_.x_ << measurement_pack.raw_measurements[0], measurement_pack.raw_measurements[1], 0, 0;
}
previous_timestamp = measurement_pack.timestamp;
is_initialized = true;
return;//仅在初始化的时候进行此步骤,初始化后结束计算,等待下次数据进入
}
/*******预测**********
TODO:
* 根据时间戳的差进行 F 矩阵的赋值
* 根据时间戳的差进行 Q 矩阵的赋值
* 使用 noise_ax, noise_ay and noise_aw估计Q
*****************/
double dt = (measurement_pack.timestamp - previous_timestamp) / 1000000.0;//deltaT
previous_timestamp = measurement_pack.timestamp;
if (dt>0)
{
ekf_.F_ << 1, 0,dt, 0,
0, 1, 0,dt,
0, 0, 1, 0,
0, 0, 0, 1;//Include delta time into the F matrix
ekf_.Q_ << 0.5*noise_ax*dt*dt*dt*dt, 0, 0, 0,
0, 0.5*noise_ay*dt*dt*dt*dt, 0, 0,
0, 0, 8, 0,
0, 0, 0, 8;//Include delta time into the Q matrix
ekf_.Predict();
}
/**********更新*********
TODO:
* 根据数据类型,进行对应的观测数据预处理并送入ekf_滤波器进行更新
* 更新对应的变换矩阵H和观测噪声矩阵R
**************************/
if (measurement_pack.sensorType == MeasurementPackage::ODOMETRY) {
// odo updates
ekf_.R_ = R_radar;
ekf_.H_ = CalculateJacobian(ekf_.x_);
ekf_.UpdateEkfRadar(measurement_pack.raw_measurements);
} else {
// visual updates
ekf_.R_ = R_visual;
ekf_.H_ = H_visual;
ekf_.Update(measurement_pack.raw_measurements);
}
}
Eigen::MatrixXd ekf_fusion2::CalculateJacobian(const Eigen::VectorXd &x_state)
{
/* Calculate a Jacobian here.*/
MatrixXd Hj = MatrixXd::Zero(3, 4);
//recover state parameters
float px = x_state(0);
float py = x_state(1);
float vx = x_state(2);
float vy = x_state(3);
float c1 = px*px+py*py;
//check division by zero
if(fabs(c1) < EPS){
std::cout << "c1 = " << c1 << std::endl;
std::cout << "CalculateJacobian () - Error - Division by Zero" << std::endl;
return Hj;
}
float c2 = sqrt(c1);
float c3 = (c1*c2);
//compute the Jacobian
Hj << (px/c2), (py/c2), 0, 0,
-(py/c1), (px/c1), 0, 0,
py*(vx*py - vy*px)/c3, px*(px*vy - py*vx)/c3, px/c2, py/c2;
return Hj;
}
除此之外,还需注意的是观察代码中分类update的过程中,出现了第二个update的函数(UpdateEkfRadar)和H的矩阵不在是个由常值组成的矩阵,变化成了会随着X值变化的雅克比矩阵。那么visual和radar的什么区别造成现在这种的现象呢?
关键在于状态变量X的设置是和visual的观测值是相同的物理意义,他们之间的转换只是部分X的值无法被观测到,X和visual中的x,y的值的物理含义是相同的,即x,y的坐标。X中的vx和vy是没有从视觉的角度进行观测。因此H矩阵只需rank为2的2*4维的单位阵即可。
状态变量X和radar的观测值的含义是完全不同的,他们之间存在非线性的变换关系,很难通过固定系数表述转换关系,这也是KF和EKF的区别。因此,H矩阵需要通过雅克比矩阵获得,雅克比矩阵可以理解为两个状态向量之间的偏导的矩阵。
在很多文章中都对雅克比矩阵一掠而过。但是在实际工程中,不总是相同的观测值哇,所以如何获得自己想要的雅克比矩阵可以按照如下的思路来。以radar的观测Z与状态X为例:

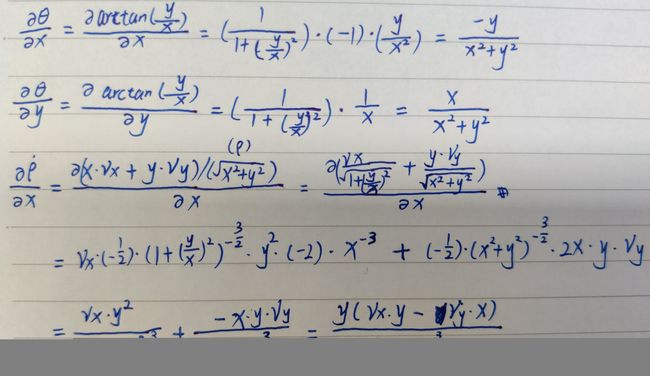

但是需要注意的是卡尔曼滤波中,H矩阵与状态X相乘可以获得与观测Z同维度的等价X的Zpred。通过观测Z与状态Zpred的差来对预测进行更新修正。
可是非线性情况下,无法通过H与X相乘获得结果。需要手工提供变换方式,即在计算观测Z与状态Zpred的差y的过程中不使用H矩阵,其他更新过程相同。
与之类似F矩阵的求解方式如下所示:
 可以将H矩阵与F矩阵的求解对照着看,也许能够更快抓住要点。
可以将H矩阵与F矩阵的求解对照着看,也许能够更快抓住要点。
在kf2.h和kf2.cpp中添加如下函数:
void kalman_filter::UpdateEkfRadar(const Eigen::VectorXd &z) {
/**
TODO:
* update the state by using Kalman Filter equations
*/
double px = X_[0];
double py = X_[1];
double vx = X_[2];
double vy = X_[3];
double rho = sqrt(px*px + py*py );
double phi = 0;
double rho_dot = 0;
if (fabs(rho) > EPS) {
phi = atan2(py , px);
rho_dot = ((px * vx + py * vy) / rho);
}
VectorXd z_pred(3);
z_pred << rho, phi, rho_dot;
VectorXd y = z - z_pred;
while (y(1) < -M_PI) {y(1) += 2 * M_PI;}
while (y(1) > M_PI) {y(1) -= 2 * M_PI;}
Eigen::MatrixXd Ht = H_.transpose();
Eigen::MatrixXd PHt = P_ * Ht;
Eigen::MatrixXd S = H_ * PHt + R_;
Eigen::MatrixXd Si = S.inverse();
Eigen::MatrixXd K = PHt * Si;
X_ = X_ + (K * y);
long x_size = X_.size();
Eigen::MatrixXd I = Eigen::MatrixXd::Identity(x_size, x_size);
P_ = (I- K * H_) * P_;
}
不带 δ t \delta t δt 的卡尔曼滤波 3D_Position+4D_Quaternion(四元数)
首先,帧对位姿(位置+姿态)的滤波需要确定状态X包含的内容,通常情况下位置滤波包含位置和速度,那么姿态滤波应该怎么设定呢?由于欧拉角的非唯一性,大多数人会考虑到旋转矩阵或者四元数作为姿态的表示方法。旋转矩阵虽然在使用时非常方便,但是对于滤波来说,旋转矩阵显然是存在信息冗余的,四元数以四个元素即可表示整个姿态信息,对于滤波计算来说显然是友好的。
但是对于卡尔曼滤波来说,隐含信息和表面信息同样重要,正是通过对隐含信息的预测和估计,实现了输出频率与采样频率相同的功能。
例如位置作为表面信息,那么速度是可以作为隐含信息。
对于姿态来说,四元数是表面信息,那么什么是隐含信息呢?
好像很难直接给出答案。
毕竟四元数的加减乘除的计算是有单独的计算方法的。
那么问题的解法不妨换个思路,四元数是否有其他等价替换方式呢?
有, θ \theta θ,nx,ny,nz的思源表示方式。其物理意义为:转动角度 θ \theta θ,转动轴的三维向量nx,ny,nz。此时,我们就可以,很方便的找到隐含信息,转动角速度,转动轴变化量。此处需要注意的一点是转动轴向量即使不进行归一化也是可以的,只要表示的等价轴是对的就行,显然轴向量的变化是连续且线性的,可以很好的适应卡尔曼滤波,唯一需要的就是从四元数到 θ \theta θ,nx,ny,nz的转换公式。
转换公式如下:
q 0 = c o s ( θ ∗ 0.5 ) q_{0}=cos(\theta*0.5) q0=cos(θ∗0.5)
q 1 = n x ∗ s i n ( θ ∗ 0.5 ) q_{1}=n_{x}*sin(\theta*0.5) q1=nx∗sin(θ∗0.5)
q 2 = n y ∗ s i n ( θ ∗ 0.5 ) q_{2}=n_{y}*sin(\theta*0.5) q2=ny∗sin(θ∗0.5)
q 3 = n z ∗ s i n ( θ ∗ 0.5 ) q_{3}=n_{z}*sin(\theta*0.5) q3=nz∗sin(θ∗0.5)
等价变换可得:
θ = 2 ∗ a r c c o s ( q 0 ) \theta=2*arccos(q_{0}) θ=2∗arccos(q0)
n x = q 1 / s i n ( θ ∗ 0.5 ) n_{x}=q_{1}/sin(\theta*0.5) nx=q1/sin(θ∗0.5)
n y = q 2 / s i n ( θ ∗ 0.5 ) n_{y}=q_{2}/sin(\theta*0.5) ny=q2/sin(θ∗0.5)
n z = q 3 / s i n ( θ ∗ 0.5 ) n_{z}=q_{3}/sin(\theta*0.5) nz=q3/sin(θ∗0.5)
注意到此处计算轴向量并没有直接利用arcsin,反而是使用 θ \theta θ作为替代。相应的也需要注意到sin0作为分母存在的风险,需要单独进行分类讨论,通常情况下的做法是轴的变化通常是连续的,既然角度没有变化,那么轴也不需要进行变动,因此保留上一时刻的轴向量的三维数值。
综上所述,位姿的X是表面信息是:x,y,z, θ \theta θ, n x n_x nx, n y n_y ny, n z n_z nz,隐含信息为: v x v_x vx, v y v_y vy, v z v_z vz, w w w, v n x v_{n_x} vnx, v n y v_{n_y} vny, v n z v_{n_z} vnz。由于在本案例中并不包含时间信息,所以隐含信息表示为 δ x \delta x δx, δ y \delta y δy, δ z \delta z δz, δ θ \delta\theta δθ, δ n x \delta n_x δnx, δ n y \delta n_y δny, δ n z \delta n_z δnz。
因此数学模型如下:

类比上面的融合步骤可以得到两个不同信号源的7元素位姿融合代码。其中由于两个信号源表述完全一致,所以H矩阵可以使用同一个,但是由于信号源不同,观测噪声R矩阵可以采用不同的矩阵。
代码原型如下:
class ekf_fusion7 {
public:
/**
* Constructor.
*/
ekf_fusion7() { init(); }
/**
* Destructor.
*/
~ekf_fusion7() {}
void init();
/**
* Run the whole flow of the Kalman Filter from here.
*/
void ProcessMeasurement(const MeasurementPackage &measurement_pack);
Eigen::VectorXd getX() {
Eigen::VectorXd res=Eigen::VectorXd(7);
double q0=cos(0.5*ekf_.X_(3));
double q1=ekf_.X_(4)*sin(0.5*ekf_.X_(3));
double q2=ekf_.X_(5)*sin(0.5*ekf_.X_(3));
double q3=ekf_.X_(6)*sin(0.5*ekf_.X_(3));
res << ekf_.X_.head(3), q0, q1, q2, q3;
return res; }
private:
/**
* Kalman Filter update and prediction math lives in here.
*/
kalman_filter ekf_;
// check whether the tracking toolbox was initiallized or not (first
// measurement)
bool is_initialized_;
// previous timestamp
long long previous_timestamp_;
// noise
double noise_ax_, noise_ay_, noise_aw_;
Eigen::MatrixXd R_odo_;
Eigen::MatrixXd R_visual_;
Eigen::MatrixXd H_odo_;
Eigen::MatrixXd H_visual_;
};
}
void ekf_fusion7::init()
{
is_initialized_=false;
// initializing matrices
//measurement covariance matrix - odometry
R_odo_ = Eigen::MatrixXd(7, 7);
Eigen::VectorXd tmp=Eigen::VectorXd(7);
tmp<<425,425,0.0,22.5,0.01,0.01,0.01;
R_odo_ =tmp.asDiagonal();
H_odo_ = Eigen::MatrixXd(7, 14);
H_odo_.setZero();
H_odo_.block(0,0,7,7)=Eigen::Matrix<double,7,7>::Identity();
//measurement covariance matrix - visual
R_visual_ = Eigen::MatrixXd(7, 7);
tmp<<425,425,0.0,22.5,0.0,0.0,0.0;
R_visual_ = tmp.asDiagonal();
H_visual_ = Eigen::MatrixXd(7, 14);
H_visual_.setZero();
H_visual_.block(0,0,7,7)=Eigen::Matrix<double,7,7>::Identity();
// Set the initial transition matrix F_
ekf_.F_ = Eigen::MatrixXd(14,14);
ekf_.F_ .setIdentity();
ekf_.F_.block(0,7,7,7) = Eigen::Matrix<double,7,7>::Identity();
//process uncertainty matrix
ekf_.P_ = Eigen::MatrixXd(14, 14);
tmp=Eigen::VectorXd(14);
tmp<<1,1,1,1,1,1,1,1000,1000,1000,1000,1000,1000,1000;
ekf_.P_ = tmp.asDiagonal();
noise_ax_=0.000005;
noise_ay_=0.000005;
noise_aw_=0.000005;
}
void ekf_fusion7::ProcessMeasurement(const MeasurementPackage &measurement_pack)
{
/*****************************************************************************
* Initialization
****************************************************************************/
if (!is_initialized_) {
/**
TODO:
* Initialize the state ekf_.x_ with the first measurement.
* Create the covariance matrix.
* Remember: you'll need to convert radar from polar to cartesian coordinates.
*/
// first measurement
ekf_.X_ = Eigen::VectorXd(14);
if (measurement_pack.sensorType == MeasurementPackage::ODOMETRY) {
// Initialize odometry state.
double q0=measurement_pack.raw_measurements(3);
double q1=measurement_pack.raw_measurements(4);
double q2=measurement_pack.raw_measurements(5);
double q3=measurement_pack.raw_measurements(6);
Eigen::VectorXd tmp=Eigen::VectorXd(7);
double theta=acos(q0)*2;
double nx,ny,nz;
if(abs(theta)<EPS|| abs(theta - M_PI) < EPS)
{
nx=ekf_.X_(4);
ny=ekf_.X_(5);
nz=ekf_.X_(6);
}
else
{
nx=q1/sin(0.5*theta);
ny=q2/sin(0.5*theta);
nz=(q3/sin(0.5*theta));
}
tmp<<measurement_pack.raw_measurements.head(3),theta,nx,ny,nz;
ekf_.X_ << tmp,0,0,0,0,0,0,0;
} else {
// Initialize vis state.
double q0=measurement_pack.raw_measurements(3);
double q1=measurement_pack.raw_measurements(4);
double q2=measurement_pack.raw_measurements(5);
double q3=measurement_pack.raw_measurements(6);
Eigen::VectorXd tmp=Eigen::VectorXd(7);
double theta=acos(q0)*2;
double nx,ny,nz;
if(abs(theta)<EPS|| abs(theta - M_PI) < EPS)
{
nx=ekf_.X_(4);
ny=ekf_.X_(5);
nz=ekf_.X_(6);
}
else
{
nx=q1/sin(0.5*theta);
ny=q2/sin(0.5*theta);
nz=(q3/sin(0.5*theta));
}
tmp<<measurement_pack.raw_measurements.head(3),theta,nx,ny,nz;
ekf_.X_ << tmp,0,0,0,0,0,0,0;
}
is_initialized_ = true;
return;
}
/*****************************************************************************
* Prediction
****************************************************************************/
/**
TODO:
* Update the state transition matrix F according to the new elapsed time.
- Time is measured in seconds.
* Update the process noise covariance matrix.
* Use noise_ax = 9 and noise_ay = 9 for your Q matrix.
*/
//set the process covariance matrix Q
ekf_.Q_ = Eigen::MatrixXd(14, 14);
ekf_.Q_.setIdentity();
ekf_.Q_(0,0)=noise_ax_*noise_ax_;
ekf_.Q_(1,1)=noise_ay_*noise_ay_;
ekf_.Q_(3,3)=noise_aw_*noise_aw_;
ekf_.Predict();
/*****************************************************************************
* Update
****************************************************************************/
/**
TODO:
* Use the sensor type to perform the update step.
* Update the state and covariance matrices.
*/
if (measurement_pack.sensorType == MeasurementPackage::ODOMETRY) {
// odo updates
ekf_.R_ = R_odo_;
ekf_.H_ = H_odo_;//CalculateJacobian(ekf_.x_);
double q0=measurement_pack.raw_measurements(3);
double q1=measurement_pack.raw_measurements(4);
double q2=measurement_pack.raw_measurements(5);
double q3=measurement_pack.raw_measurements(6);
Eigen::VectorXd tmp=Eigen::VectorXd(7);
double theta=acos(q0)*2;
double nx,ny,nz;
if(abs(theta)<EPS|| abs(theta - M_PI) < EPS)
{
nx=ekf_.X_(4);
ny=ekf_.X_(5);
nz=ekf_.X_(6);
}
else
{
nx=q1/sin(0.5*theta);
ny=q2/sin(0.5*theta);
nz=(q3/sin(0.5*theta));
}
tmp<<measurement_pack.raw_measurements.head(3),theta,nx,ny,nz;
ekf_.Update7d(tmp);
} else {
// visual updates
ekf_.R_ = R_visual_;
ekf_.H_ = H_visual_;
double q0=measurement_pack.raw_measurements(3);
double q1=measurement_pack.raw_measurements(4);
double q2=measurement_pack.raw_measurements(5);
double q3=measurement_pack.raw_measurements(6);
Eigen::VectorXd tmp=Eigen::VectorXd(7);
double theta=acos(q0)*2;
double nx,ny,nz;
if(abs(theta)<EPS|| abs(theta - M_PI) < EPS)
{
nx=ekf_.X_(4);
ny=ekf_.X_(5);
nz=ekf_.X_(6);
}
else
{
nx=q1/sin(0.5*theta);
ny=q2/sin(0.5*theta);
nz=(q3/sin(0.5*theta));
}
tmp<<measurement_pack.raw_measurements.head(3),theta,nx,ny,nz;
ekf_.Update7d(tmp);
}
}