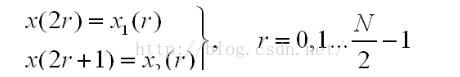基4fft算法的蝶形图_fft基-2 dit算法
如果觉得本文章对你有用,请麻烦点个赞,谢谢。
--------------------------------------------------
fft基-2 dit算法
首先,只要先介绍一下DFT,名称叫做离散傅里叶变换,作用是将时域上的信号转换成频域上的信号。这个变换的序列是有限长的。其中为旋转因子,具有一定的特性。根据公式给出的计算公式:
可以看出来,他的时间复杂度为。这样的计算量和时间十分的冗长,而我们的FFT算法的目的就是为了简化DFT的复杂度,将时间复杂度变成O(log2N)是一种优化形式。FFT的算法有很多种,大概的思想是把一次大的DFT分割成几个小的DFT,这样递归式地细分下去……。我用的这个是Radix-2 dit。
Radix-2 dit其实就是将众多的序列,根据时间序列的方式,按照奇偶分别分为两组的形式:
同时,我们还可以利用旋转因子的一些特性:
这样就达到了对DFT进行分解。
这样就可以将一个序列为N的DFT换成两个序列为N/2的DFT,然后就一直化成N/2个序列为2的DFT。
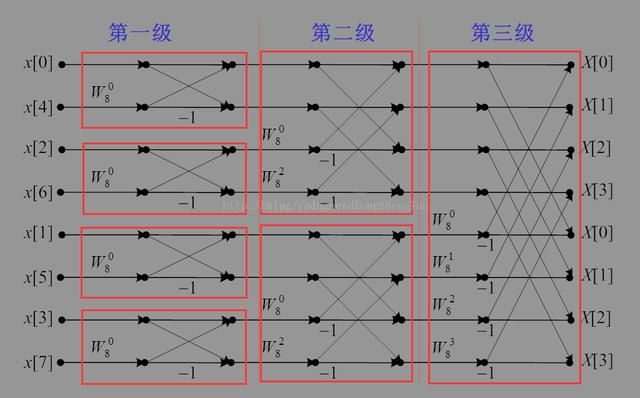
最后用一个直观图(蝶形运算图)来观察计算式:
源代码
#include
#include
#define N 8
#define M 3
#define PI 3.14159
typedef struct { /*定义复数结构体*/
float real;
float image;
}complex;
void daoxu(int a[N]) //定义倒叙函数,运用雷德算法 (当顺位序数小于倒位序数,进行换序)
{
int i,j,k,n1,t,lh;
n1=N-1;
lh=N/2;
j=0; //j为倒位序数
for(i=0;i
{
if(i
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
k=lh; //k相当于 100.... ,接下来求j的倒位序
while(j>=k) //如果j的最高位为1,进入循环体
{
j=j-k; //将1变为0
k=k/2; //k变成 010...
}
j=j+k; //最高位数为0,置1,得到j的倒位序
}
}
void outarray(complex x[N]) //定义打印数组函数
{
int j;
printf("下面输出结构体数组:");
for(j=0;j
{
printf("%f+i*(%f) ,",x[j].real,x[j].image);
}
printf("");
}
complex add(complex a,complex b) //定义复数加法
{
complex s;
s.real =a.real +b.real ;
s.image =a.image +b.image ;
return s;
}
complex sub(complex a,complex b) //定义复数减法
{
complex s;
s.real =a.real -b.real ;
s.image =a.image -b.image ;
return s;
}
complex mul(complex a,complex b) //定义复数乘法
{
complex s;
s.real =a.real*b.real-a.image*b.image ;
s.image =a.image*b.real+a.real *b.image ;
return s;
}
void fft(complex x[N])
{
int i,j,l,k,b,p;
complex wnp={0.0},ak={0.0},akb={0.0},product={0.0};
for(l=1;l<=log(N)/log(2);l++) //控制蝶形的级数
{
b=pow(2,l-1); //b为第l级的旋转因子个数,也为蝶形的间隔
for(i=0;i<=b-1;i++) //控制第l级旋转因子乘法的次数,有多少个旋转因子就乘多少次
{
p=i*pow(2,M-l); //计算出WNP的P
wnp.real=cos(2*PI*p/N); //用欧拉公式计算旋转因子
wnp.image=-sin(2*PI*p/N);
for(j=i;j<=N-1;j=j+pow(2,l)) //计算同一个旋转因子,计算一个蝶形算法
{ //第一级循环4次,第二级循环两次,第三级循环一次,....;
product=mul(wnp,x[j+b]);
ak=add(x[j],product); //两点的DFT运算
akb=sub(x[j],product) ;
x[j]=ak;x[j+b]=akb;
}
}
}
}
main()
{
printf("******************************************************************************");
printf(" 现在进行的是基-2-dit算法");
printf("******************************************************************************");
int x1[N],i;
complex a[N],b[N],x[N];
for (i=0;i
x1[i]=i;
printf ("正序结果:");
for (i=0;i
printf("%4d",x1[i]);
printf("");
daoxu(x1);
printf ("倒叙结果:");
for(i=0;i
{
printf("%4d",x1[i]);
}
printf("");
printf ("现在请输入时间序列的信号函数:");
printf ("形如:a+b*i,请输入a b");
for (i=0;i
{
printf ("现在进行第%d个函数的输入:",i+1);
scanf("%f %f",&b[i].real,&b[i].image);
}
printf ("读入完毕.");
for (i=0;i
{
a[i]=b[x1[i]];
}
for (i=0;i
{
x[i]=a[i];
}
printf("现在输出时间序列的结果:");
outarray(x) ;
printf("进行基2 DIT算法的傅立叶变换");
fft(x) ;
printf("将时域上的时间信号转换成频域上的信号");
outarray(x) ;
}