目标跟踪 ATOM（ATOM: Accurate Tracking by Overlap Maximization）

文章标题：《ATOM: Accurate Tracking by Overlap Maximization》
文章地址：https://arxiv.org/pdf/1811.07628.pdf
github地址：https://github.com/visionml/pytracking

CVPR 2019 的一篇文章。
主要作者之一叫做 Martin Danelljan，据说是做跟踪方面的大佬、数学大佬。

---

Abstract

虽然近年来，视觉跟踪任务的鲁棒性（robustness）有了惊人的提升，但是准确度（accuracy）仍然进步不大。人们把专注于开发强大的分类器，但是严重忽略了准确的目标状态估计（target state estimation)(也就是包围框的回归问题）。实际中，许多分类器采用简单的多尺度搜索方法（例如 SiamFC）来估计目标的包围框。我们认为这种方法本质上是局限的，因为目标估计是一个很复杂的事情，需要有该目标的高层次信息（high-level knowledge）。

我们提出了一个新颖的跟踪架构来解决这个问题，该架构由专门的目标估计（target estimation）和分类（classification）组件构成。通过广泛的离线学习，把高层次信息融入到目标估计中。我们训练目标估计组件，用于预测目标和估计出来的包围框之间的 overlap。通过精心地整合 target-specific information ，我们的方法达到了前所未有的包围框准确度。我们进一步介绍了一个分类组件，是在线训练的，用于保证受到干扰时能有强大的分辨能力。

本算法在 $5$ 个具有挑战性的基准上都刷到了 state-of-the-art，在大型数据集 TrackingNet 上，我们的跟踪器 ATOM 比先前的 No.1 提高了接近 $15\%$，运行速度在 $30\text{FPS}$ 以上。

1 Introduction

在线跟踪是个很难的问题，算法必须在最小的 supervision（监督）下在线学习目标的外观模型（appearance model ），通常是在视频的第一帧做这件事。 模型要对没有见过的方面具有泛化能力，包括不同的姿态，视角，光照等。跟踪任务可以分解为一个分类（classification）任务和一个估计（estimation ）任务。对于前者，要通过把图像区域划分为前景和背景，从而鲁棒地提供目标的粗略定位。后者是估计目标状态，通常用一个边界框表示。

当前的问题：
近年来，大家都关注于目标分类、构建鲁棒的分类器。例如某些基于相关滤波器（correlation filters）的方法，还有某些利用深度特征表示的方法。另一方面，目标估计的进展不及预期，可以从 VOT2018 的竞赛结果上观察到，像比较老的 KCF 和 MEEM 跟踪器还排名很前，然而它们的鲁棒性其实远不如人意。实际中，最近比较先进的跟踪器仍然依赖于分类组件，通过多尺度搜索来估计目标状态。然而这种策略本质上很受限，因为边界框的估计是一个很有挑战性的问题，需要理解目标的高维信息。

本文做法：
(1)包围框的预测
本文中，我们平衡了目标分类和目标估计之间的性能差距，我们引入了一个新颖的跟踪架构，由专门的目标估计和目标分类两部分组成。受到最近的 IoU-Net 的启发，我们训练一个目标估计组件 ，来预计 “目标” 和 “估计出来的包围框” 之间的 IoU。由于原始的 IoU-Net 是特定类别的（class-specific 的），所以它对于通用目标跟踪不是非常合适，我们提出了一个新颖的架构把 target-specific 的信息融入到 IoU 的预测中。 我们用过引入一种基于调制的（modulation-based）网络组件，把 reference 的图像（也就是模板）的目标外观信息结合起来，以获得 target-specific 的 IoU 估计。这使得我们在大规模数据集上离线训练目标估计组件。在跟踪的过程中，通过把预测得到的 IoU overlap 最大化，来找到目标包围框。

(2)在线训练分类器 （用共轭梯度在线训练）
为了开发一个无缝的透明的跟踪方法，我们也重新讨论了目标分类问题，以避免不必要的复杂性。我们的目标分类组件简单且强大，由 $2$ 个全连接层的网络头组成。与目标估计模块不同，分类组件是在线训练的，在受到干扰的场景下提供强鲁棒性。为了保证实时性能，我们解决了在线优化时，无法高效地梯度下降的问题。相反，采用了基于共轭梯度的策略，还演示了如何在深度学习架构中实现它。跟踪流程很简单，主要包括分类、估计、模型更新。

效果：
在 NFS、UAV123、LaSOT、VOT2018、TrackingNet 这 $5$ 个数据集全部刷到了 state-of-the-art，在 LaSOT 上以 $10\%$ 的绝对值领先。

2 Related work

在视觉跟踪领域，通常把目标分类（target classification）和目标估计（target estimation）分成两个既独立，又关联的子任务。目标分类是判定 “目标在某一图像位置是否存在” 。然而能给到该任务的信息很少，例如只有图像坐标。目标估计要找到它的完整状态，通常是用包围框来表示。在最简单的情况下，目标是刚性的，只在画面中做平移。这时目标估计可以简化为寻找它在二维图像中的定位，于是不需要与目标分类任务分开考虑。 然而实际情况要复杂得多，物体的视角和姿态会发生根本性变化，导致包围框的估计变得复杂。

过去几年，通过在线训练强大的分类器，目标分类问题得到很好的解决，特别是基于相关滤波（correlation-based）的跟踪器得到广泛应用。但是一直以来都无法精确地估计目标（包围框）。即使要找到一个单参数的尺度因子，也是一个巨大的挑战。大多数方法都采用蛮力多尺度检测的策略，计算负担很大。因此，默认的方法是用一个单独的分类器来做状态估计。但目标分类器不是对目标状态的所有方面都敏感，例如宽度和高度。实际上，目标状态在某些方面具有不变性，可以考虑利用这个特性来提高模型的鲁棒性。我们不依赖于分类器，而是学习一个专门的目标估计组件。

对于目标包围框的精确估计，是一个复杂的任务，需要有高级的先验知识。边界框依赖于目标的姿态和视角，这不能被建模为一个简单的图像变换（例如统一的图像缩放）。因此，从零开始在线学习准确的目标估计是非常具有挑战性的。最近有一些方法，通过大量的离线训练来整合先验知识。例如 SiamRPN，还有它的延伸算法，都展现了包围框回归的能力。然而这些暹罗（siamese）跟踪方法通常在目标分类问题上挣扎。 不像那些基于相关（correlation-based）的方法，暹罗跟踪由于没有做在线更新，没有明确地考虑干扰因素。虽然有的使用简单的模板更新技术，改善了一点点，但它还没有达到强大的在线学习模型的水平。与暹罗跟踪方法相比，我们在线学习分类模型，同时利用了大量的离线训练来进行目标估计任务。

3 Proposed Method

本文提出的跟踪方法由两部分组成：（1）离线训练的目标估计模块。（2）在线训练的目标分类模块。
这两部分集成在一个统一的多任务网络结构中。

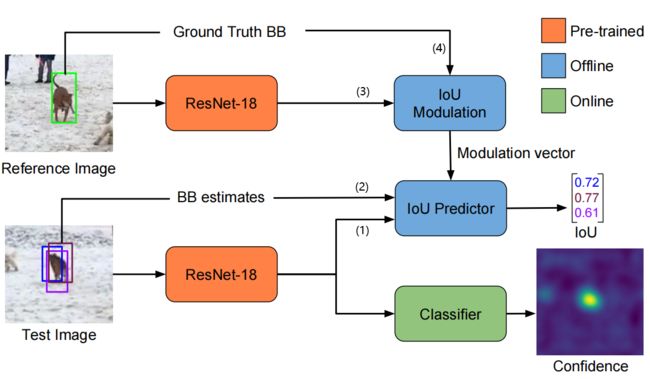
(图2)

图 $2$：我们在 预训练 的 ResNet-18 骨干网络上添加了两个模块。目标估计 模块是在大规模数据集上离线训练的，用来预测目标的 IoU overlap。IoU Modulation 模块使用参考图像（reference image）和初始目标框，计算出带有特定目标外观信息（target-specific appearance information）的调制向量（modulation vectors）。IoU Predictor 模块从测试图片拿到深度特征和建议的包围框，以及上面来的调制向量，估计每一个包围框的 IoU。目标分类 模块是在线训练的，用全卷积的方式输出目标置信度。

目标分类和目标估计 任务共用同一个骨干网络，这个骨干是在 ImageNet 上预训练的 ResNet-18，然后在这里微调。

目标估计 模块用的是 IoU-perdictor 网络，这个网络是用大规模视频跟踪数据集和目标检测数据集离线训练的，在跟踪的时候冻结权重。
IoU-perdictor 有 $4$ 个输入：
⑴ 当前帧的骨干网络特征；
⑵ 当前帧的估计的包围框；
⑶ 参考图的骨干网络特征；
⑷ 参考图的目标包围框(也就是你选定的框)。
它为每一个 “在当前帧估计的包围框” 预测 IoU 得分。
在跟踪过程中，通过梯度上升最大化 IoU 得分，获得最终的包围框。

目标分类 用了另外一个头，它是完全在线学习的。它经过专门的训练，使用当前帧的骨干网络特征，预测目标的置信度分数，从而把跟踪目标从场景里和其它东西区分出来。训练和预测都用全卷积的方式，以保证效率和覆盖范围，在线训练这样一个网络不太容易，像随机梯度下降这类传统的方法是很不理想的。于是我们提出了一种优化策略，它基于 共轭梯度 和 高斯-牛顿 法，可以在线快速训练。我们还用 PyTorch 实现了前向传播和反向传播，很容易使用。

3.1 Target Estimation by Overlap Maximization

这一节详细介绍目标估计模块。目标估计模块的目的是，确定目标包围框，给定粗略的初始估计。我们用到了 IoU-Net，与传统的方法相比，IoU-Net 用于预测 “目标真实框” 和 ”输入的候选框” 之间的 IoU，然后通过最大化 IoU 的预测来实现包围框的估计。

为了更好地描述目标估计模块，这里先简单复习一下 IoU-Net。给定：
① 图像的深度特征表示：$x\in {\mathbb{R}}^{W\times H\times D}$
② 目标的包围框估计：$B\in {\mathbb{R}}^4$
IoU-Net 预测 $B$ 和目标之间的 IoU。

这里 $B$ 的参数化表示为 $B=\left(\frac{c_x}{w},\frac{c_y}{h},\log w,\log h\right)$，其中 $(c_x,c_y)$ 是包围框中心点的坐标。
该网络使用 Precise ROI Pooling（PrPool），根据 $B$ 的坐标，对特征 $x$ 中对应的区域进行池化，得到指定大小的特征图 $x_B$。 PrPool 是一种自适应平均池化，它的变量是连续的，关键优点是对于包围框坐标 $B$ 是可微的。这使得我们可以通过梯度上升来最大化 IoU，从而优化包围框 $B$。

Network Architecture：
在目标检测任务中，对于每个类别的目标都要单独训练一个 IoU-Net。然而在跟踪任务里，目标类别一般是未知的。另外，一般来说，被跟踪的目标不属于预先定义的类，在训练集里也没有出现过。所以特定类别（class-specific）的 IoU 预测器在这里用处不大。相反，我们需要特定目标（target-specific）的 IoU 预测，用到的数据是第 $1$ 帧的标注。由于 IoU 预测任务是 high-level 的，在单帧数据上，在线训练或者微调 IoU-Net 都是不太行的。因此我们认为目标估计网络需要离线训练，学习一般特征表示用于 IoU 预测。

要跟踪的对象是事先未知的，因此难点是有效地利用参考图像来构建 IoU 预测架构。我们最开始的实验表明，把 “参考图像的特征” 和 “当前图像的特征” 简单地融合起来性能很差。同时也发现用 Siamese 的架构得到次优的结果。于是我们提出了一种基于调制（modulation-based）的网络结果，仅根据一张参考图片，可以预测任意目标的 IoU。该架构如图(3)所示。

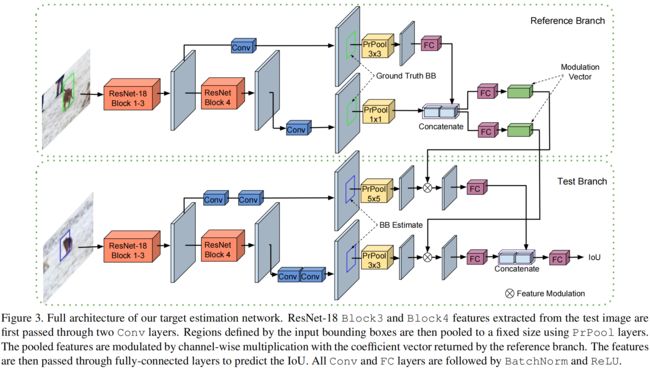
(图3)

图 $3$：目标估计网络的完整结构。测试图片进入 ResNet-18，然后从 Block3 和 Block4 出来深度特征。出来的特征先各自经过两个卷积层 Conv（蓝色那两块）。然后用 PrPool 层把建议的区域池化到固定的尺寸。Reference Branch 出来的调制向量（Modulation Vector）其实是个 $1\times 1$ 的系数向量，用它对前面讲的池化后的特征进行通道上的相乘。再把这个特征输入到全连接层来预测 IoU。所有的 Conv 层和 FC 层都加了 BatchNorm 和 ReLU。

我们的网络有两个支路，两个支路都是用 ResNet-18 的 Block3 和 Block4 的输出作为输入。
reference 支路的输入是特征 $x_0$ 和选定的包围框 $B_0$，它返回一个调制向量 $c(x_0,B_0)$，尺寸是 $1\times 1\times D_z$，值是一些正的系数。

test 支路要对当前图片估计出目标的包围框。它首先用 backbone 提取特征 $x$， 然后把它传进两个卷积层，然后根据估计的包围框 $B$ ，用 PrPool 提取深度特征。由于 test 支路要为 IoU 的预测提取一般特征，这是一个更复杂的任务，与 reference 支路相比，它使用了更多的层和更高分辨率的 pooling。得到的特征表示 $z(x,B)$ 的尺寸是 $K\times K\times D_z$，$K$ 是 PrPool 层输出的空间尺寸。然后对从测试图片计算出来的特征表示进行调制（modulate），做法是用系数向量 $c$ 对它做通道上的（channel-wise）乘法。这就为 IoU 的预测提供了目标特定（target-specific）的表示。调制后的向量传进 IoU 预测模块 $g$，该模块是由 $3$ 个全连接层组成的。对包围框 $B$ 的 IoU 预测公式如下：$$\text{IoU}(B)=g\left(c(x_0,B_0)\cdot z(x,B)\right)\text{\hspace{1em}(1)}$$ 根据标注的数据，通过最小化公式(1)的预测误差来训练网络。跟踪的时候，根据 $B$ 来最大化公式(1)，以估计目标状态。

Training：
从公式(1)可以看到，只要能选择一对（pairs）标注了包围框的图片，整个 IoU 预测网络就能够进行端到端的训练。我们用的是 LaSOT 和 TrackingNet 的训练集，选择的图片最大间隔是 $50$ 帧。我们从 COCO 数据集构造一些图片对，泛化更多的类别，作为数据增强。在参考图像中，我们以目标为中心裁剪一个正方形的图块，它的面积是目标（标注框）面积的 $5$ 倍。对于测试图片，裁剪一个差不多的图块，但是中心点和大小稍微有点抖动，这样可以模拟真实跟踪场景。最后这些裁剪的图块都 resize 成固定的大小。对于每一对图像，通过对标注框添加高斯噪声，生成 $16$ 个候选框，同时保证 IoU 大于 $0.1$。还用了翻转和颜色增强。和 IoU-Net 一样，IoU 归一化到 $[-1,1]$。

网络头的权重采用 MSRA 初始化，backbone 的权重在训练时一直冻住。损失函数是平均平方误差（MSE），训练 $40$ 个 epochs，每个 epoch $64$ 个图像对。优化器用的 ADAM，初始学习率 $10^{-3}$，每 $15$ 个 epoch 乘以系数 $0.2$。

3.2 Target Classification by Fast Online Learning

虽然目标估计模块提供了准确的边界框输出，但是缺乏能力鲁棒地把目标从干扰背景中区分出来。我们用第二个网络头作为目标估计的补充，它只有一个目的，就是做区分。与估计组件不同，目标分类模块是专门在线学习的，用来预测目标的置信度得分。由于目标分类模块的任务是粗略地提供目标的 $2\text{D}$ 位置，我们希望它与尺寸和比例无关（invariant）。相反，它应该通过最小化误检来强调鲁棒性。

Model：
我们的目标分类模块是一个 $2$ 层的全卷积网络，公式定义为：$$f(x;w)={\varphi }_2\left(w_2\ast {\varphi }_1\left(w_1\ast x\right)\right)\text{\hspace{1em}(2)}$$其中， $x$ 是 backbone feature map，$w=\{w_1,w_2\}$ 是网络参数，${\varphi }_1$ 和 ${\varphi }_2$ 是激活函数，$\ast$ 表示标准的多通道卷积（multi-channel convolution）。这个架构是通用的，你可以换更复杂的模型。我们发现这样一个简单的模型是足够的，在计算高效性中获益。

受 DCF 的启发，我们基于 $L_2$ 分类误差制定了类似的学习目标：$$L(w)=\sum _{j=1}^m{\gamma }_j\Vert f(x_j;w)-y_j{\Vert }^2+\sum _k{\lambda }_k\Vert w_k{\Vert }^2\text{\hspace{1em}(3)}$$每个训练样本（特征图 $x_j$） 都用分类置信度 $y_i\in {\mathbb{R}}^{W\times H}$ 来标注，它是一个以目标为中心的高斯分布采样（sampled Gaussian function）。在损失函数中，每个训练样本的影响用权重 ${\gamma }_j$ 来控制，参数 $w_k$ 的正则化力度设为 ${\lambda }_k$。

Online Learning：
要最小化公式(3)，一种简单粗暴的方法是使用标准梯度下降或者随机梯度下降。用现成的深度学习框架很容易实现这些方法，但是不适合在线训练，因为收敛速度很慢。我们为此开发了一种更复杂的优化方法，专门针对这种在线学习的问题，实现起来只有一点点复杂。首先，把问题的残差（residuals）定义为：
$$\begin{array}{rl}& r_j(w)=\sqrt{r_j}\left(f(x_j;w)-y_j\right),j\in \{1,\dots ,m\}\\ & r_{m+k}(w)=\sqrt{{\lambda }_k}{w}_k,k=1,2\end{array}$$（这个很简单，残差是原函数的导数）

于是公式(3)的损失函数等价于残差向量的 $L^2$ 范数：$L(w)=\Vert r(w){\Vert }^2$。
其中 $r(w)$ 是所有残差 $r_j(w)$ 的 concatenation。

我们利用二次高斯-牛顿（Gauss-Newton）近似：${\tilde{L}}_w(\Delta w)\approx L(w+\Delta w)$。
它可以通过在当前估计 $w$ 上对残差 $r$ 做一阶泰勒展开（ $r(w+\Delta w)\approx r_w+J_w\Delta w$ ）来获得，把它代进去得：
$${\tilde{L}}_w(\Delta w)=\Delta w^T{J}_w^T{J}_w\Delta w+2\Delta w^T{J}_w^T{r}_w+r_w^T{r}_w\text{\hspace{1em}(4)}$$

这里我们已经有定义 $r_w=r(w)$，以及 $J_w=\frac{\partial r}{\partial w}$ 是 $r$ 在 $w$ 处的雅克比（Jacobian）。新的变量 $\Delta w$ 表示参数 $w$ 的增量。

这个高斯-牛顿子问题（式子(4)） 形成了一个正定二次方程，使得我们可以用一些特殊的机制，例如共轭梯度（Conjugate Gradient，CG）。关于 CG 的完整描述不在本文范围内，直观来说，它就是要在每一次迭代中找到一个最优的搜索方向 $p$ 和步长 $\alpha$。由于 CG 算法是由一些简单的向量操作组成的，可以用几行 python 代码搞定。唯一的挑战就是要为搜索方向 $p$ 计算式子 $J_w^T{J}_{w}p$。

我们知道 CG 已经在一些 DCF 的跟踪器上成功地应用了，然而，这些方案依赖于对所有操作手撸代码来实现 $J_w^T{J}_{w}p$，即使对于简单的模型（如 式子(2)）也需要花许多时间求导，乏味地工作。而且也缺乏灵活性，要是 式子(2) 有细微的修改，例如加了一层、改变了非线性，那么你又要重新求导、手撸代码实现。

本文证明了如何为 式子(4) 实现共轭梯度，通过采用深度学习框架（例如 PyTorch）中的反向传播函数。我们的实现仅需要使用者提供 $r(w)$ 以计算残差，这很容易实现。因此，我们的算法适用于任何形式的像 式子(3) 这样的浅层学习问题。

为了找到一种策略以计算 $J_w^T{J}_{w}p$，我们首先考虑一个向量 $u$，它的尺寸与 $r(w)$ 相同。通过计算它们内积后的残差，我们得到：$$\frac{\partial }{\partial w}\left(r(w{)}^{T}u\right)={\frac{\partial r}{\partial w}}^{T}u=J_w^{T}u$$
事实上，这是反向传播过程的标准操作，即在计算图中的每个节点上应用转置的雅可比矩阵，从输出端开始。
于是我们可以把一个标量方程 $s$ 关于变量 $v$ 的反向传播定义为 $\text{BackProp}(s,v)=\frac{\partial s}{\partial v}$。
综上，我们有 $\text{BackProp}(r^{T}u,w)=J_w^{T}u$，然而，这只解决了 $J_w^T{J}_{w}p$ 里面的第二个乘法，我们首先要计算 $J_{w}p$，这涉及到雅可比矩阵本身的应用（不是它的转置）。幸运的是，函数 $u\mapsto J_w^{T}u$ 简单地就是 $J_w^T$，因为这个方程是线性的。因此，我们可以通过应用反向传播来转置它。令 $h:=J_w^{T}u=\text{BackProp}(r^{T}u,w)$，我们得到 $J_{w}p=\frac{\partial }{\partial u}(h^{T}p)=\text{BackProp}(h^{T}p,u)$。

基于以上结果，我们给出了完整的优化过程：

(算法 1)

它使用 $N_{GN}$ 次高斯-牛顿迭代，每个迭代里包含 $N_{CG}$ 次共轭梯度迭代（用于最小化子问题 式子(4)）。
每个共轭梯度迭代里面需要调用两次 $\text{BackProp}$ 来分别计算 $q_1=J_{w}p$ 和 $q_2=J_w^T{q}_1$。
在外部循环中，需要计算一次 $h=J_w^{T}u$。

算法(1) 中每次 $\text{BackProp}$ 的调用，都把内积中的其中一个向量当做常数，即，反向传播梯度的时候不会经过它。为了清晰起见，这在 算法(1) 中用了注释来突出显示。

值得注意的是，该优化算法实际上是无参数的，不需要调参，只需要设置迭代次数。与梯度下降相比，基于共轭梯度的方法在每次迭代中自适应地计算学习率 $\alpha$ 和动量 $\beta$。注意观察到，$g$ 是 式子(4) 的梯度的负数。

3.3 Online Tracking Approach

我们的 ATOM 跟踪器使用 PyTorch 实现的，在 Nvidia GTX-1080 单卡上运行速度超过 $30\text{FPS}$。

Feature extraction:
我们用 ImageNet 上预训练的 ResNet-18 作为骨干网络。对于目标分类（target classification），我们用了 block 4 的特征。目标估计（target estimation）部分用的 block 3 和 block 4 作为输入。特征（Features）是来自于 $288\times 288$ 的图像上的一块区域来的，这块区域的大小是所选目标区域的 $5$ 倍。注意的是，ResNet-18 提取的特征是共享的，在每一帧只提取 $1$ 个图像块的特征。

Classification Model:
分类头（式子(2)）的第一层由 $1\times 1$ 的卷积层 $w_1$ 组成，它将特征的维度降低至 $64$。和 ECO 的做法一样，这一层的目的是降低内存和计算开销。第二层采用了一个 $4\times 4$ 的卷积核 $w_2$，输出通道为 $1$。我们令 ${\varphi }_1$ 为 $1$ （identity），因为我们观察到，在这一层用非线性没有获得任何收益。我们用连续可导的 PELU（parameteric exponential linear unit） 作为输出激活：
$${\varphi }_2=\{\begin{array}{ll}t,& t\ge 0\\ \alpha \left(e^{\frac{t}{\alpha }}-1\right),& t\le 0\end{array}$$

用 $\alpha =0.05$ 可以使我们忽略损失（式子(3)）中的易分类负样本（easy negative examples）。我们发现 ${\varphi }_2$ 的连续可微性有利于优化。

在第 $1$ 帧中，我们通过应用不同程度的平移（translation）、旋转（rotation）、模糊（blur）和丢弃（dropout）来作为数据增强，从而得到 $30$ 个初始训练样本 $x_j$。
然后用 算法(1) 来优化参数 $w$，设 $N_{GN}=6$，$N_{CG}=10$。
然后，只优化最后一层的 $w_2$， 每 $10$ 帧用 $N_{GN}=1$，$N_{CG}=5$。
每帧里我们用特征图 $x_j$ 作为训练样本，它的标注是基于估计目标中心的高斯分布 $y_j$
。式子(3) 里的权重 ${\gamma }_j$ 用学习率 $0.01$ 来更新。

Target Estimation:
我们首先在先前估计的目标位置和尺寸上提取特征。然后应用分类模型（式子(2)），根据最大的置信度得分来找到 $2\text{D}$ 位置。与之前估计的目标宽度和高度一起，生成初始包围框 $B$。虽然可以使用这种单一的建议（proposal）来进行状态估计，但我们发现使用多个随机初始化可以更好地避免局部极大值。因此，我们通过在 $B$ 中加入均匀的随机噪声，来生成一组 $10$ 个初始建议（proposals)。通过使用步长为 $1$ 、迭代 $5$ 次的梯度上升来最大化每个框预测的 IoU（式子(1)）。最终的预测方法是取 IoU 最高的 $3$ 个包围框的平均值。没有进一步的后处理或者过滤。注意 式子(1) 中的调制向量 $c(x_0,B_0)$ 是在第 $1$ 帧里预先计算好的。

Hard Negative Mining:
为了在有干扰物（distractors）的场景下进一步增强分类组件的鲁棒性，我们采用了难分类负样本挖掘策略。（hard negative mining strategy）。

如果在分类得分里检测到了干扰物峰值，我们就把这个训练样本的学习率 double，然后立即使用标准设置（$N_{GN}=1$，$N_{CG}=5$）跑一轮优化。

如果目标得分低于 $0.25$，我们就判定为目标跟丢了。

虽然这个策略不是我们这个框架的基本结构之一，但是能够提供一些额外的鲁棒性。

4 Experiments

我们在 $5$ 个基准上评估 ATOM：Need for Speed（NFS），UAV123，TrackingNet，LaSOT，VOT2018。
详细结果在补充材料里。

实验自己看原文…