连续数列问题-分治法 详解
面试题 16.17. 连续数列–分治法 详解 （附完整版C语言代码）
分治法解题步骤详细解答，含时间复杂度推导过程。
题目
`给定一个整数数组，找出总和最大的连续数列，并返回总和。
示例：
输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。
一、分治法思想原理
（1） 分治法基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题相互独立且与原问题相同。
（2）递归的解这些子问题，然后将各子问题的解合并得到原问题的解。
总而言之，分治法的过程为 " 分—治—合并 " 。
二、用分治法的思想解答本题
1.如何分：
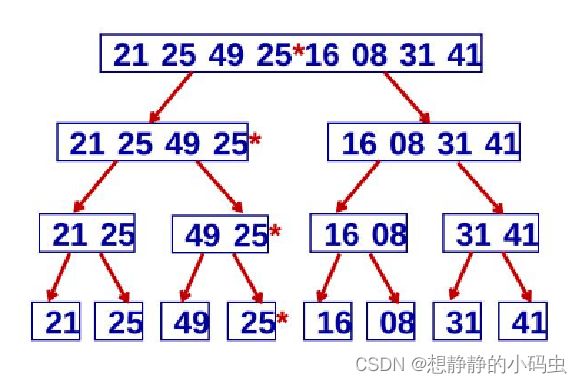
随机举例（如下图），数组[21，25，49，25，16，08，31，41]，通过不断的递归，将数组分为单元素数组。
代码如下（示例）：
int subMax( int * nums , int left , int right ){
// 递归终止的条件
if( left >= right ){
return *( nums + left );
}
int mid = left + ( right - left ) / 2;
//仅求中点左部分和
int left_sum = subMax( nums , left , mid );
//求跨越中点的和
int mid_sum = crossMid( nums , left , mid , right );
//求中点右部分和
int right_sum = subMax( nums , mid + 1 , right );
return max( left_sum , max( right_sum , mid_sum ) );
}
2.如何治：
分为单元素数组后，一目了然，最大值就是它本身。
3.如何合并（难点）：
如何合并是这道题目的难点。难点在于子数组合并成长数组时，长数组的最大值该如何得到。
（1）合并的思想原理：
两个规模相等的子数组A[ low…mid ] 和 A [ mid+1…high ]合并为一个长数组 A [ low…high ]，其中 mid=(low+high)/2。那么，和最大的连续子数组必定位于以下三种位置之一：
（1）完全位于左子数组中：
（2）完全位于右子数组中：
（3）跨越中点：
这三种情况取最大值就是合并后的长数组的解。
（2）单元素数组合并为双元素数组的情况：
用红色方框内的单元素数列合并为双元素序列举例：数组[4]、[-1]合并为数组[4，-1]
按照合并的原理：
完全位于左子数组：left_sum=4
完全位于右子数组：right_sum=-1
跨越中点（两边都有包含只可能是[4,1]）：cross_sum=4+(-1)=3
取三种情况的最大值，返回到上一层，作为上一层的 right_sum/left_sum
（3）多元素数组合并的情况：
用红色方框内举例：数组[-2,1,-3]与[4,-1]合并为数组[-2,1,-3,4,-1]
按照合并的原理：
完全位于左子数组：left_sum=-2 （由底一层递归得到）
完全位于右子数组：right_sum=4（同上）
跨越中点？
多元素跨越中点的情况怎么求？（重点）
由中线 mid 向左右两边延展，对左右两边分别循环遍历，一个个相加，再比较。分别找出[i…mid]与[mid+1…j]的最大值，再相加即可。
//求中点左半部分和
for( int i = mid ; i >= left ; i-- ){
// 逐渐向左加，每次加一个数
sum += *( nums + i );
// 找到更大的和，就覆盖原先的和
if( sum > left_sum ){
left_sum = sum;
}
}
合并过程如下图：
三、分治法时间复杂度推导
把一个数据量为 n 的问题分为 a(a>1)个形式相同的子问题，这些子问题的规模为 n/b，如果分解或者合并的复杂度为 f(n)，那么总的时间复杂度可以表示为：
用上面的求解方式都是递推求解，写出其递推式，最后求出结果。
4、完整的C语言代码
#include