基于遗传算法的卷积神经网络架构搜索
论文推荐：基于遗传算法的卷积神经网络架构搜索
来自文章 《Evolving Deep Convolutional Neural Networks for Image Classification》
这篇文章于2019年发表在IEEE Transactions on Evolutionary Computation上，文章提出了一种使用遗传算法来进行卷积神经网架构搜索的方法。文章主要可以分为三个部分：第一部分介绍卷积神经网络发展背景以及一些基本知识，第二部分提出了基于遗传算法的神经网络架构搜索的具体实现细节，第三部分设计实验验证自己的算法并在主要的一些数据集上与当前一些主流算法做了对比。
第一部分
在这部分作者阐述了一些有关卷积神经网络的一些基础知识，比如卷积层，池化层，全连接层等我在这里就不再赘述了，以后如果有机会的话我也许会专门写一篇文章来讲一讲这些东西。需要注意的是，在这一部分作者还提出了使用遗传算法来设计卷积神经网络架构时会遇到的一些问题：
（1）在对一个架构进行性能评估之前是无法判断一个架构的好坏的，然而性能评估需要很长的时间。如果是对整个群体进行性能评估，那所需要的的时间和算力更是巨大的。
（2）卷积神经网络的深度是不确定的，因此很难约束搜索空间。
（3）神经网络的权重初始化值严重影响已确定的网络架构结构的性能，解决这一问题需要良好的基因编码策略并完成成百上千个决策变量的优化。
废话不多，下面直接上算法。
第二部分 基于遗传算法的卷积神经网络架构搜索
Gene Encoding Strategy
作者将卷积神经网络按块分为3类，即卷积层，池化层和全连接层。染色体由这三类块平行编码组成。考虑到卷积神经网络的深度是不可知的，作者采用了可变长的编码策略。下图给出的是三条不同长度的染色体。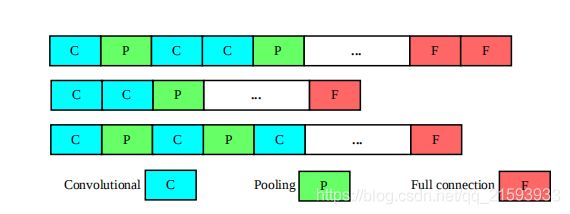
在卷积层和全连接层存在着大量的连接权重，染色体不可能表示所有参数并且对其进行优化。针对这一问题，作者指出仅使用连接权重的平均值和标准差这两个统计量来表示大量的权重参数。当我们得到最佳的平均值和标准差之后，可以在相应的高斯分布中取样以获取对应的连接权重。作者还给出了每一模块所需要表示的信息：
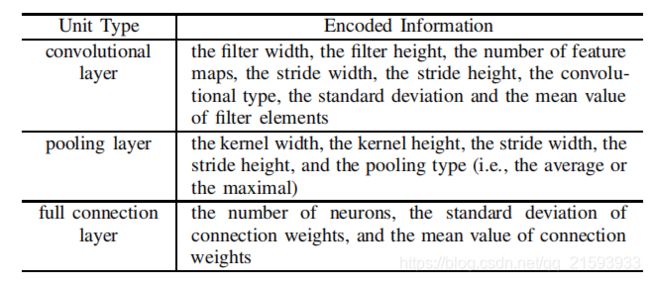
Population Initialization
在进行种群初始化时，作者将每一个染色体分成两个部分，第一个部分包括卷积层和池化层，第二部分是全连接层。作者的策略是首先初始化第一部分，第一部分初始化完成后再初始化第二部分。
在初始化第一部分时，首先向第一部分中加入一个所有参数都随机初始化的卷积层，然后不断随机以1/2概率向向第一部分中加入一个所有参数都是随机初始化的卷积层或者所有参数都是随机初始化的池化层，直至第一部分块的数量达到预定数量。
在初始化第二部分时，不断向向第二部分中加入一个所有参数都是随机初始化的全连接层，直至第二部分块的数量达到预定数量。
当着两部分都完成之后，将这两部分组合起来得到一个染色体。算法的伪代码如下所示：
Input: The population size N N N, the maximal number of convolutional and pooling layers N c p N_{cp} Ncp, and the maximal number of full connection layers N f N_{f} Nf .
Output: Initialized population P 0 P_{0} P0.
P 0 ← ∅ P_{0}\leftarrow\varnothing P0←∅
while ∣ P 0 ∣ ≤ N \left | P_{0}\right |\leq N ∣P0∣≤N do
p a r t 1 ← ∅ \qquad part_{1}\leftarrow\varnothing part1←∅
n c p ← \qquad n_{cp}\leftarrow ncp←Uniformaly generate an integer between [ 1 , N c p ] \left [1,N_{cp} \right] [1,Ncp]
\qquad while ∣ p a r t 1 ∣ ≤ n c p \left |part_{1}\right|\leq n_{cp} ∣part1∣≤ncp do
r ← \qquad \qquad r\leftarrow r←Uniformly generated a number between [ 0 , 1 ] \left [0,1\right] [0,1];
\qquad \qquad if r ≤ 0.5 r\leq0.5 r≤0.5then
l ← \qquad \qquad \qquad l\leftarrow l←Initialize a convolutional layer with random settings;
\qquad \qquad else
l ← \qquad \qquad \qquad l\leftarrow l← Initialize a pooling layer with random settings;
\qquad \qquad end
p a r t 1 ← p a r t 1 ∪ l \qquad \qquad part_{1}\leftarrow part_{1}\cup l part1←part1∪l
\qquad end
p a r t 2 ← ∅ \qquad part_{2}\leftarrow\varnothing part2←∅
n f ← \qquad n_{f}\leftarrow nf←Uniformaly generate an integer between [ 1 , N f ] [1, Nf ] [1,Nf];
\qquad while ∣ p a r t 2 ∣ ≤ n f |part_{2}|\leq n_{f} ∣part2∣≤nf do
l ← \qquad \qquad l\leftarrow l← Initialize a full connection layer with randomsettings;
p a r t 2 ← p a r t 2 ∪ l \qquad \qquad part_{2}\leftarrow part_{2}\cup l part2←part2∪l
\qquad end
P 0 ← P 0 ∪ ( p a r t 1 ∪ p a r t 2 ) \qquad P_{0}\leftarrow P{0}\cup(part_{1}\cup part_{2}) P0←P0∪(part1∪part2)
end
Return P 0 P_{0} P0
fitness evaluation
在该算法中，作者采取了三个指标来衡量每条染色体的质量。即卷积网络用于图像分类时的误差的平均值，误差的标准差和卷积神经网络中连接权值的数量。
为了节省时间和计算资源，作者对于每一条染色体（一个卷积神经网络）仅训练5个或者10个epochs。按照作者的说法，如果一个神经网络在最初的几个epochs内表现出了良好的性能，那么在以后的训练中，该神经网络仍然会保持优良的性能，关于原理，作者并未解释。
因为一次同时处理的数据有限，所以验证时validation dataset被分成多份依次处理，作者计算训练后的神经网络在每一个batch上的误差的平均值和标准差作为衡量染色体性能的指标，除此之外作者还将神经网络中连接权值的数量作为一个指标，作者提出更少的连接权重对于智能设备来说是十分重要的。算法的伪代码如下所示：
Input: The population p t p_{t} pt, the training epoch number k k k for measuring the accuracy tendency, the training set D t r a i n D_{train} Dtrain, the fitness evaluation dataset D f i t n e s s D_{fitness} Dfitness, and the batch size n u m _ o f _ b a t c h num\_of\_batch num_of_batch.
Output: The population with fitness Pt.
for e a c h i n d i v i d u a l s i n P t each\ individual\ s\ in P_{t} each individual s inPt do
i ← 1 \qquad i\leftarrow 1 i←1;
e v a l _ s t e p s ← ∣ D f i t n e s s ∣ / n u m _ o f _ b a t c h \qquad eval\_steps\leftarrow |D_{fitness}|/num\_of\_batch eval_steps←∣Dfitness∣/num_of_batch;
\qquad while i ≤ k i\leq k i≤k do
\qquad \qquad Train the connection weights of the CNN
represented by individual s s s;
\qquad \qquad If i = = k i==k i==k then
a c c c y _ l i s t ← ∅ \qquad \qquad \qquad acccy\_list\leftarrow\varnothing acccy_list←∅
j ← 1 \qquad \qquad \qquad j\leftarrow 1 j←1
\qquad \qquad \qquad while j ≤ e v a l _ s t e p s j\leq eval\_steps j≤eval_steps do
a c c y j ← \qquad \qquad \qquad \qquad accy_{j}\leftarrow accyj←Evaluate the classification error
on the j j j-th batch data from D f i t n e s s D_{fitness} Dfitness;
a c c y _ l i s t ← a c c y _ l i s t ∪ a c c y j \qquad \qquad \qquad \qquad accy\_list\leftarrow accy\_list \cup accy_{j} accy_list←accy_list∪accyj
j ← j + 1 \qquad \qquad \qquad \qquad j\leftarrow j+1 j←j+1
\qquad \qquad \qquad end
\qquad \qquad \qquad Calculate the number of parameters in s s s, the mean value and \qquad \qquad \qquad standard derivation from a c c y l i s t accy_{list} accylist, assign them to individual s \qquad \qquad \qquad s s, and update s from P t P_{t} Pt;
\qquad \qquad end
i ← i + 1 \qquad \qquad i\leftarrow i+1 i←i+1;
\qquad end
end
Return P t P_{t} Pt
Slack Binary Tournament Selection
作者采用Slack Binary Tournament Selection来选择下一代个体的双亲。适应度有三个方面：连接权重矩阵参数个数，分类的平均错误率和其标准差。选择的时候要兼顾。
在选择时首先考虑分类误差，如果两条染色体的分类误差之差大于给定的阈值，那么就将分类误差较低的一条染色体放入交配池，否则考虑权值参数的数量，如果两条染色体的权值参数的数量之差大于给定的阈值，那么就将参数数量较少的一条染色体放入交配池，最后考虑分类误差的标准差，优先选择标准差小的那条染色体。伪代码如下：
Input: Two compared individuals, the mean value threshold α \alpha α, and the paramemter number threshold β \beta β.
Output: The selected individual.
s 1 s_{1} s1:The individual with larger mean value;
s 2 s_{2} s2 ← The other individual;
μ 1 , μ 2 \mu_{1},\mu_{2} μ1,μ2← The mean values of s 1 , s 2 s_{1},s_{2} s1,s2;
s t d 1 , s t d 2 std_{1},std_{2} std1,std2 ← The standard derivations of s 1 , s 2 s_{1},s_{2} s1,s2;
c 1 , c 2 c_{1},c_{2} c1,c2 ← The parameter numbers of s 1 , s 2 s_{1},s_{2} s1,s2;
if μ 1 − μ 2 > α \mu_{1}-\mu_{2}>\alpha μ1−μ2>α then
\qquad Return s 1 s_{1} s1.
else
\qquad if c 1 − c 2 > β c_{1}-c_{2}>\beta c1−c2>β then
\qquad \qquad Return s 2 s_{2} s2.
\qquad else
\qquad \qquad if s t d 1 < s t d 2 std_{1}
\qquad \qquad \qquad Return s 1 s_{1} s1
\qquad \qquad else if s t d 1 > s t d 2 std_{1}>std_{2} std1>std2 then
\qquad \qquad \qquad Return s 2 s_{2} s2
\qquad \qquad else
\qquad \qquad \qquad **Return*random one from s 1 , s 2 {s_{1},s_{2}} s1,s2.
\qquad \qquad end
\qquad end
end
Offspring Generation
分为四步：
- 从交配池（mating pool）中随机选择两个个体（parents）
- 交叉算子应用于指定的两个父辈个体上，生成后代（offspring）
- 在offspring上使用变异算子
- 存储两个新生成的子代个体并将两个父辈个体从mating pool中移除。重复1-3，直至mating pool为空。
crossover
由于不同的染色体长度是不同的，作者提出了一种新的交叉运算方法，该方法主要分为3步：
- Unit Collection (UC)，将每条染色体中的卷积层，池化层，全连接层按照原来的排列顺序分别放到不同的lists当中去，这样2条染色体会得到6个lists。
- Unit Alignment(UA)，将这2条染色体中的相同的unit(比如卷积层）按头对其，并执行交叉运算，如下图所示。
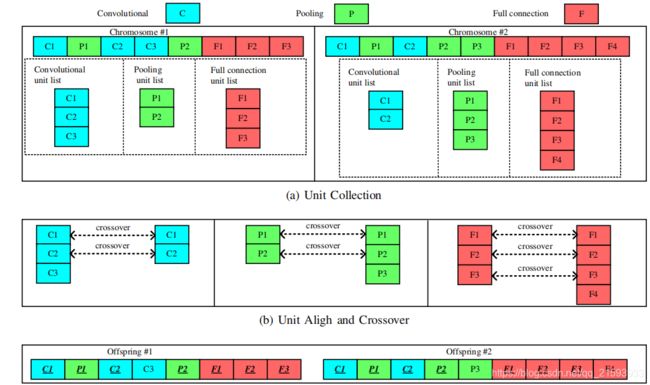3. Unit Restore (UR)，完成交叉操作后，两条染色体按照原来排列顺序组装成两条新的染色体。
Mutation
对于选定的基因，分别按照1/3的概率进行删除，修改或者增加一个新的基因。
Environmental Selection
作者综合考虑了种群中的精英部分和种群的多样性，自然选择由两部分组成。第一部分首先按照给定的参数选选出一部分最优的染色体放入种群。第二部分是在剩下的染色体之中使用改进的二元锦标赛选择法选择染色体放入种群。
实验设计与验证
首先介绍使用的数据集，作者将9个数据集分为三类：
- Fashion
手写数字识别MNIST 及其变种： - the MNIST Basic (MB) --MNIST数据集
- the MNIST with Background Images (MBI) --带背景图
- Random Background(MRB) --带随机背景图
- Rotated Digits (MRD) --旋转数字
- with RD plusBackground Images (MRDBI) [50] benchmarks.–既旋转又带背景图
识别图形形状 - the Rectangle
- the Rectangle Images (RI)
- the ConvexSets (CS)
在第一类数据集上，作者与其他10个网络做了对比，作者给出了下面的数据：
好像也只有VGG16和GooleNet的准确率好于作者提出的算法的平均准确率，但是他们的参数数量都要远远大于EvoCNN，这样看来，EvoCNN是一个综合性能很不错的网络了。
对于其他两类数据集作者也与另外12个常见网络做了对比，总体来说性能还是很不错的。值得注意的是，作者还进一步研究了初始化方法对于网络分类精度的影响。对于同一个网络架构，做个采用了两种初始化方法，一种是作者提出的EvoCNN approach方法，另一种是目前比较常用的 Xavier initializer，在一些主要的数据集上，作者得到了下面的结果。
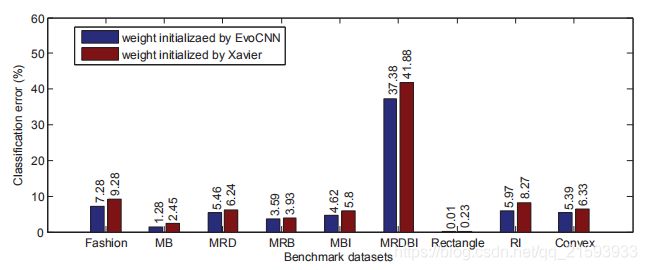由此可见，权值初始化对于分类精度也是有影响的，但其影响程度远不如网络架构对分类精度来的明显。而作者提出的算法无论在网络架构还是权值初始化上都有着比较优异的性能。
ok,以上就是这篇论文的主要内容，最后作者提出了他的论文的三大特色：
- 使用可变长的编码策略。
- 没有使用梯度下降法，避免了算法陷入局部最优解。使用平均值与方差解决了染色体难以表示大量参数的问题。
- 对神经网络进行训练时仅仅训练了很少个epochs,并用训练结果来预测神经网络的最终性能，这样既节约了时间又节省计算资源。