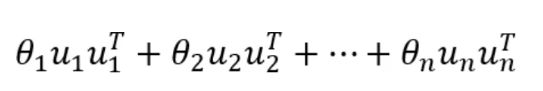沈华伟老师图卷积神经网络教学视频笔记
图卷积神经网络
- 感谢
- 0. 背景介绍
-
- 基于图的应用
-
- node-level
- graph-level
- singal-level
- 数据集介绍
-
-
- 1. Cora数据集:
- 2. CiteSeer
- 3. Pubmed
-
- 1. CNN
-
-
- 1.1 CNN有效的原因
-
- 2. 从基于欧式数据的网络迁移到非欧数据上
-
- 2.1 主要困难
- 2.2 目标
- 3. 卷积
-
- 数学中的卷积(信号处理中的卷积)
-
- 连续量卷积
- image上的卷积
- 总结:卷积是一种对信号的处理方式
- 图卷积的两种方法:
-
-
- Spectral method (谱方法)
-
- 特点:
- 问题:
- Spatial method (空间方法)
-
- 特点:
- 基本思想:
- 挑战:
- 图卷积神经网络的输入输出
-
-
-
- 基本知识:图,邻居,度矩阵,邻接矩阵
-
-
- Spectral method (谱方法)的实现
-
- I: 工具 → \rightarrow → Graph Laplacian(图上的拉普拉斯变换)
-
- 意义:
- II: Graph Fourier Transform
- Define Convolution in spectral domian
- Spectral Graph CNN
-
- 但这个方法实际不可用:
- ChebyNet: parameterizing filter
-
- Parameterizing convolution filter via polynomial approximation
- Graph Wavelet Neural Network
-
-
- 存在问题:
- 实验结果:
- 小波基有很好的图可解释性
- 补充介绍数据集
-
-
- Spatial methods for graph convolutional neural networks
-
- Learning Convolutional Neural Networks for Graphs. ICML, 2016
-
-
- By analogy(使用类比的方法,将CNN迁移到Graph上)
-
- Inductive Respresentation Learning on Large Graphs. NeuralPS 2017
-
- GraphSAGE
- Semi-supervised classification with graph convolutional networks, ICLR2017
-
- GCN(Graph Convolutional Network)
- Graph Attention Network, ICLR2018
-
- GAT(Graph Attention Network)(简写GAN已经被生成对抗网络占了...)
- Geometric deep learning on graphs and manifolds using mixture model CNNs (2016)
-
- MoNet: A general framework for spatial methods
- 2019 IJCAI graph convolution networks using heat kernal for Semi-supervised Learning
-
-
- 谱方法是空间方法的一个特例:
- Graph signal processing: filter
-
- 对信号 x x x在某图上的平滑程度进行测量
- Basic filters
- Combine filters
- GCN 只考虑k=0, k=1 的情况
- 低通滤波器
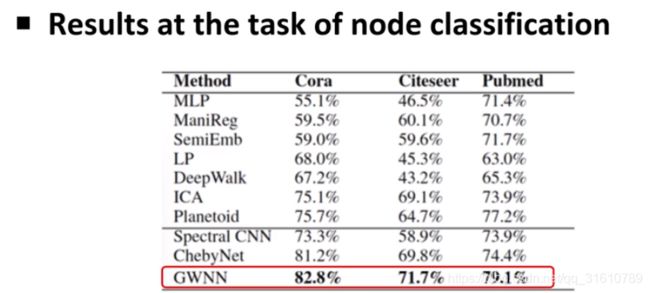
- Compared with baseline methods
-
- Neighborhood
-
- Graph pooling
-
- 讨论
-
- 1
-
- 2. 上下文表示学习的体现
- 3. 未来应用
- 回答问题:
感谢
非常感谢沈华伟老师在B站的教学视频,讲得真棒,这里是对该视频的学习笔记。整理出来,如有侵权请及时联系我。
教学视频链接: https://www.bilibili.com/video/BV1ta4y1t7EK
ps. 评论区上传视频的小伙伴留下了讲义的网盘链接
0. 背景介绍
基于图的应用
node-level
节点预测:根据若干已有标签的节点和图结构预测目标节点的标签(社交网络用户分类,节点异常检测)
链路预测:预测节点对之间的链路的存在或者出现
graph-level
图分类:通过图卷积网络学习一个图的表达对图进行分类(子图分类生物信息领域,分蛋白质网络,基因网络;诈骗软件识别)
singal-level
信息分类:类似image,认为image是一个网络结构从来不变的栅格图,变化的是信息。(交通方面,交通流量是signal)
数据集介绍
1. Cora数据集:
样本特征,标签,邻接矩阵
该数据集共2708个样本点,每个样本点都是一篇科学论文,所有样本点被分为8个类别,类别分别是1)基于案例;2)遗传算法;3)神经网络;4)概率方法;5)强化学习;6)规则学习;7)理论
每篇论文都由一个1433维的词向量表示,所以,每个样本点具有1433个特征。词向量的每个元素都对应一个词,且该元素只有0或1两个取值。取0表示该元素对应的词不在论文中,取1表示在论文中。所有的词来源于一个具有1433个词的字典。
每篇论文都至少引用了一篇其他论文,或者被其他论文引用,也就是样本点之间存在联系,没有任何一个样本点与其他样本点完全没联系。如果将样本点看做图中的点,则这是一个连通的图,不存在孤立点。
2. CiteSeer
在CiteSeer数据集中,论文分为六类:Agents、AI(人工智能)、DB(数据库)、IR(信息检索)、ML(机器语言)和HCI,共包含3312篇论文,记录了论文之间引用或被引用信息。去除停用词和在文档中出现频率小于10次的词,整理得到3703个唯一词。CiteSeer数据集包含两个文件:.content文件和.cites文件,其中.content文件描述论文信息的格式为:
但是,Citeseer数据集中的分类太笼统。
3. Pubmed
PubChem是美国国立卫生研究院(NIH)的开放化学数据库,是世界上最大的免费化学物信息集合。
PubChem的数据由数百个数据源提供,包括:政府机构,化学品供应商,期刊出版商等。
21世纪的毒理学(Tox21)计划是NIH,环境保护局和食品药品管理局的联邦合作计划,旨在开发更好的毒性评估方法。目标是快速有效地测试某些化合物是否有可能破坏人体中可能导致不良健康影响的过程。Tox21数据集是其中一个比赛用到的数据集,包含了12个毒理试验测定的化学合成物质的结构信息
雌激素受体α,LBD(ER,LBD)
雌激素受体α,full(ER,full)
芳香
芳烃受体(AhR)
雄激素受体,full(AR,full)
雄激素受体,LBD(AR,LBD)
过氧化物酶体增殖物激活受体γ(PPAR-γ)
核因子(红细胞衍生的2)样2 /抗氧化反应元件(Nrf2 / ARE)
热休克因子反应元件(HSE)
ATAD5
线粒体膜电位(MMP)
P53
每个毒理实验测试的都是PUBCHEM_SID从144203552-144214049共10486个化合物,包括环保化合物、一些上市药物等物质的活性结果。
1. CNN
CNN与TCN在image, text, audio, video广泛应用。
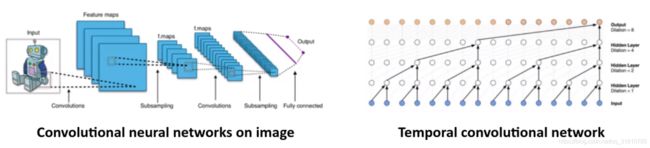
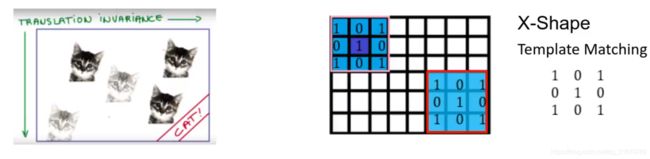
1.1 CNN有效的原因
- 通过 localized convolution filter 学习到 local stationary structures
- multi-scale hierarchical patterns (层级堆叠)
- 参数共享
- 具有 平移不变性 的数学特征
当年 GNN -> CNN 重要一步就是 参数共享
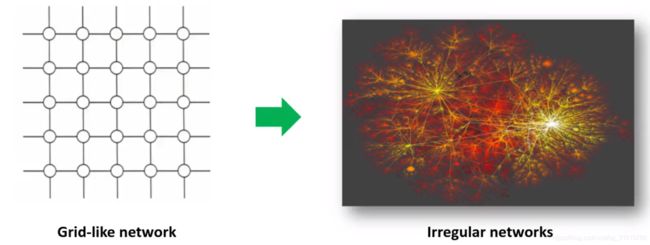
2. 从基于欧式数据的网络迁移到非欧数据上
2.1 主要困难
2.2 目标
- 定义图上的卷积
- 定义图上的pooling
3. 卷积
数学中的卷积(信号处理中的卷积)
连续量卷积
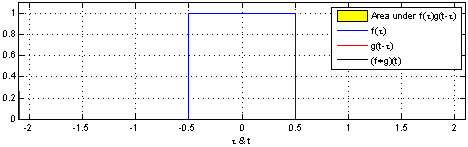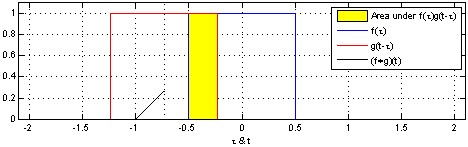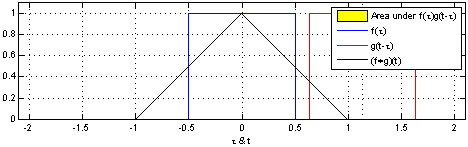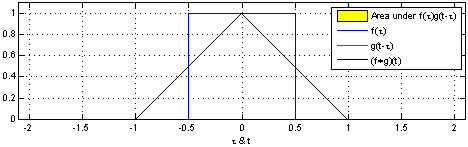
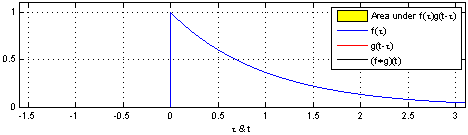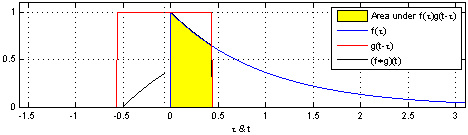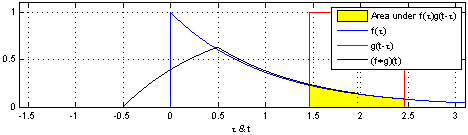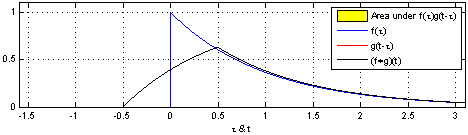
h ( t ) = ( f ∗ g ) ( t ) = d e f ∫ f ( t ) g ( t − τ ) d τ h(t)=(f*g)(t) \overset{def}{=}\int f(t)g(t-\tau)d\tau h(t)=(f∗g)(t)=def∫f(t)g(t−τ)dτ
说明:使用一个单周期方波进行卷积,输出为重叠面积,g(t)成为卷积核。
该过程从信号处理角度称之为:使用g(t-tao)处理f(tao)。
效果:信号变得平滑,(调制解调中的调制过程,实现模拟信号的通信)
作用:处理时域上的信号,是一种积分。
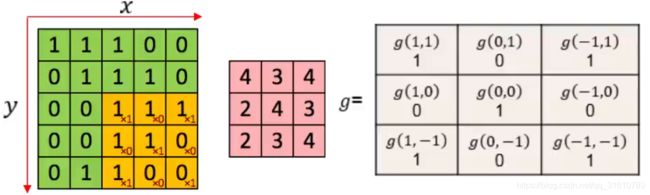
image上的卷积
h ( x , y ) = ( f ∗ g ) ( x , y ) = d e f ∑ m , n f ( x − m , y − n ) g ( m , n ) h(x,y) \\=(f*g)(x,y) \\ \overset {def}{=}\sum_{m,n}{f(x-m,y-n)g(m,n)} h(x,y)=(f∗g)(x,y)=def∑m,nf(x−m,y−n)g(m,n)
总结:卷积是一种对信号的处理方式
图卷积的两种方法:
Spectral method (谱方法)
特点:
- 在谱域中定义。而非在节点域定义子模板
- 将图上的信号变换到谱域上。
- 在谱域上实现卷积的定义
- 根据卷积的性质,变回到空间域
问题:
- 谱域上的卷积核在节点域上并非localized.
Spatial method (空间方法)
特点:
- 在节点域直接定义子模板
基本思想:
- 定义在一个目标节点的所有领域节点的加权平均
挑战:
- 每个节点的邻居度不同,如何定义一个大小一样的邻域,来实现参数共享(之后的GCN,GAT都在解决这个问题)
图卷积神经网络的输入输出
基本知识:图,邻居,度矩阵,邻接矩阵
Given a graph G = ( V , E , W ) G=(V,E,W) G=(V,E,W)
- V V V : 节点集合,个数为 n = ∣ V ∣ \vert V\vert ∣V∣
- E E E : 边的集合
- W W W : 边上的权重集合, W ∈ R n × n W \in R^{n \times n} W∈Rn×n
- d d d: 每个节点有一个d维的特征,
- X X X:输入的特征矩阵为 X ∈ R n × d X \in R^{n \times d} X∈Rn×d , 可看作是一种信号
Spectral method (谱方法)的实现
I: 工具 → \rightarrow → Graph Laplacian(图上的拉普拉斯变换)
Graph Laplacian详细说明:
https://zhuanlan.zhihu.com/p/56568843
意义:
-
定义了图上的导数,刻画图上信号的平滑程度
公式:
L = D − W L=D-W L=D−W
D i i = ∑ j W i , j D_{ii} =\sum_{j} W_{i,j} Dii=j∑Wi,j
解释: 对角线的度矩阵 D D D减去带权的邻接矩阵 W W W -
标准化的 L L L
L = I − D − 1 2 W D − 1 2 L=I-D^{-\frac{1}{2}} WD^{-\frac{1}{2}} L=I−D−21WD−21
II: Graph Fourier Transform
- Fourier basis of graph G
根据谱方法的目标,需要将信息投影到谱域上,使用拉普拉斯矩阵来构造这组基。
L = U Λ U T L=U\Lambda U^T L=UΛUT
where U = [ u 1 , . . . , u n ] U=[u_1,...,u_n] U=[u1,...,un], Λ = d i a g ( [ λ 1 , . . . , λ n ] ) \Lambda=diag([\lambda_1,...,\lambda_n]) Λ=diag([λ1,...,λn])
L n × n L^{n\times n} Ln×n的n个特征向量是正交的,对应n个基 { u } l = 1 n \{u\}^{n}_{l=1} {u}l=1n, l l l :表示第几层。
- Graph Fourier Transform
所以现在目标是将 X X X投影到这组基上。
这里先以 d = 1 d=1 d=1 为例,此时输入的信息 x x x可以简单看作是一个n维向量 x ∈ R n x\in{R^{n}} x∈Rn。
Graph Fourier transform:
x ^ = u T ⋅ x \hat{x}=u^T\cdot x x^=uT⋅x
Graph Fourier inverse transform:
x = u ⋅ x ^ x=u\cdot \hat{x} x=u⋅x^
Define Convolution in spectral domian
-
在信号处理中,有个定理:两个信号的卷积的傅里叶变换=它们傅里叶变换后的点积,此处也是如此定义:
x ∗ G y = U ( ( U T x ) ⊙ ( U T y ) ) x*_Gy=U((U^Tx)\odot (U^Ty)) x∗Gy=U((UTx)⊙(UTy))
x x x是输入信号, y y y是节点域上的卷积核, U T y U^Ty UTy 是谱域上的卷积核。 -
令:
U T y = [ θ 1 , . . . , θ n ] T U^Ty=[\theta_1,...,\theta n]^T UTy=[θ1,...,θn]T
g θ = d i a g ( [ θ 1 , . . . , θ n ] ) g_\theta=diag([\theta_1,...,\theta n]) gθ=diag([θ1,...,θn])
则:
x ∗ G y = U ( ( U T x ) ⊙ ( U T y ) ) x*_Gy=U((U^Tx)\odot (U^Ty)) x∗Gy=U((UTx)⊙(UTy))
⇓ \Downarrow ⇓
x ∗ G y = U g θ U T x x*_Gy=Ug_\theta U^Tx x∗Gy=UgθUTx
公式中看作走了三步:
图傅里叶变换: U T x U^Tx UTx
使用 g θ g_\theta gθ作为filter,在谱域上进行卷积: g θ U T x g_\theta U^Tx gθUTx
图傅里叶逆变换回到节点域: U g θ U T x Ug_\theta U^Tx UgθUTx
完成了图上的,基于谱方法的图卷积神经网络(2014提出,谱方法的奠基性作用)
Spectral Graph CNN
x k 1 , j = h ( ∑ i = 1 f k U F k , i , j U T x k , i ) x_{k_1, j} = h\biggl(\sum_{i=1}^{f_k} UF_{k,i,j}U^Tx_{k,i}\biggr) xk1,j=h(i=1∑fkUFk,i,jUTxk,i)
x k , i x_k,i xk,i : Signals in k-thlayer
F k , i , j F_{k,i,j} Fk,i,j: Filter in the k-th layer
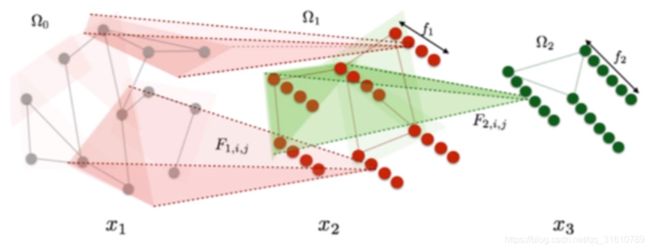
但这个方法实际不可用:
- Laplacian matrix 的 eigen-decomposition(特征值分解) 复杂度很高为 O ( n 3 ) O(n^3) O(n3)
- 使用Fourier basis U U U( U U U 十分稠密) 对信号 x x x做变换的时候,复杂度为 O ( n 2 ) O(n^2) O(n2) ,(使用在社交网络上无法承受)
- 在节点域上并非localized
ChebyNet: parameterizing filter
(2016 nips)
Parameterizing convolution filter via polynomial approximation
通过多项式近似的方法, 将谱域上的自由的卷积核 g θ g_\theta gθ进行参数化
g θ = d i a g ( [ θ 1 , . . . , θ n ] ) g_\theta=diag([\theta_1,...,\theta n]) gθ=diag([θ1,...,θn])
⇓ \Downarrow ⇓
g β ( Λ ) = ∑ k = 0 K − 1 β k Λ k Λ = d i a g ( λ 1 , . . . , λ n ) g_\beta(\Lambda)=\sum_{k=0}^{K-1}\beta_k \Lambda^k\ \ \ \ \ \ \ \ \Lambda=diag(\lambda_1,...,\lambda_n) gβ(Λ)=k=0∑K−1βkΛk Λ=diag(λ1,...,λn)
ChebyNet :
x ∗ G y = U g β ( Λ ) U T x = ∑ k = 0 K − 1 β k L k x x*_Gy=Ug_\beta(\Lambda)U^Tx=\sum_{k=0}^{K-1}{\beta_k L^k x} x∗Gy=Ugβ(Λ)UTx=k=0∑K−1βkLkx
谱域上的filter g θ g_\theta gθ自由参数量从 n → K n \rightarrow K n→K
优点:
- 不用计算 U U U
- L L L是一个稀疏矩阵
- 复杂度降低: O ( n 3 ) O(n^3) O(n3) → \rightarrow → O ( ∣ E ∣ ) O(\vert E\vert ) O(∣E∣), ∣ E ∣ = \vert E\vert= ∣E∣=边的个数。
- 由 L L L的 k k k次幂, L L L具有localized特性:对于一个中心节点,其卷积只受K跳邻域的影响。
补:大于K跳的位置的矩阵元素为0
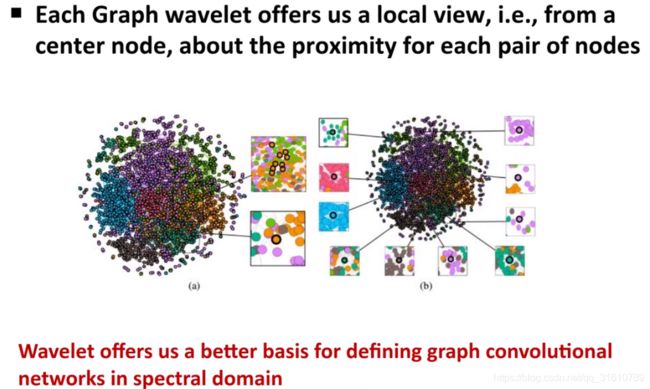
Graph Wavelet Neural Network
不同于ChebyNet着眼于 g θ g_\theta gθ,该种方法着眼于 U U U, U U U有很多上述说明的缺点(稠密,not localized, 计算复杂度高)
使用wavelet bisis 替代Fourier bisis
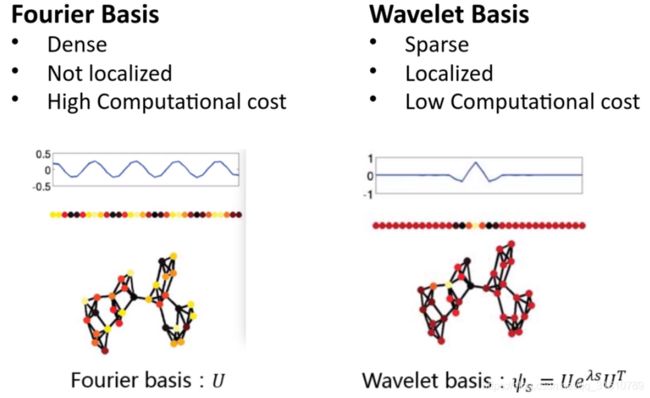
替换后:
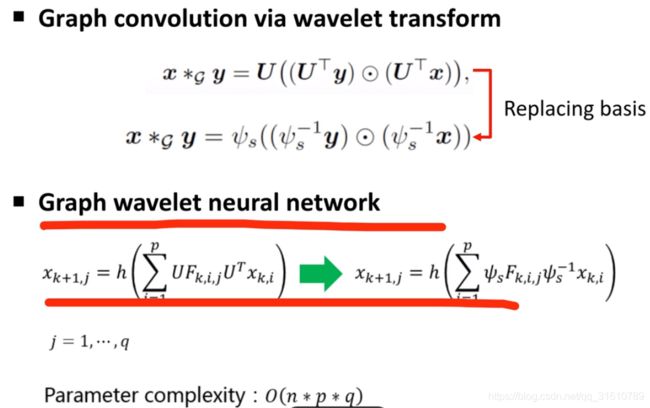
存在问题:
实验结果:
小波基有很好的图可解释性
| 数据集 | 来源 | #图 | #节点特征 | #边 | #特征 | #标签(y) |
|---|---|---|---|---|---|---|
| Cora | “Collective classification in network data,” AI magazine,2008 | 1 | 2708 | 5429 | 1433 | 7 |
| Citeseer | “Collective classification in network data,” AI magazine,2008 | 1 | 3327 | 4732 | 3703 | 6 |
| Pubmed | “Collective classification in network data,” AI magazine,2008 | 1 | 19717 | 44338 | 500 | 3 |
补充介绍数据集
Spatial methods for graph convolutional neural networks
谱方法是空间方法的一个特例。
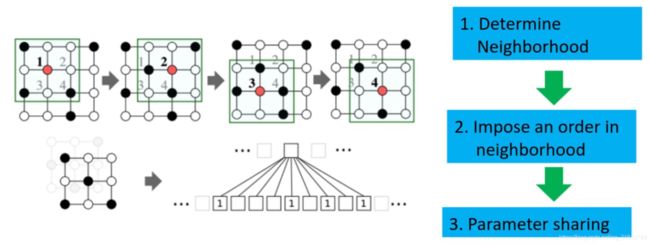
Learning Convolutional Neural Networks for Graphs. ICML, 2016
By analogy(使用类比的方法,将CNN迁移到Graph上)
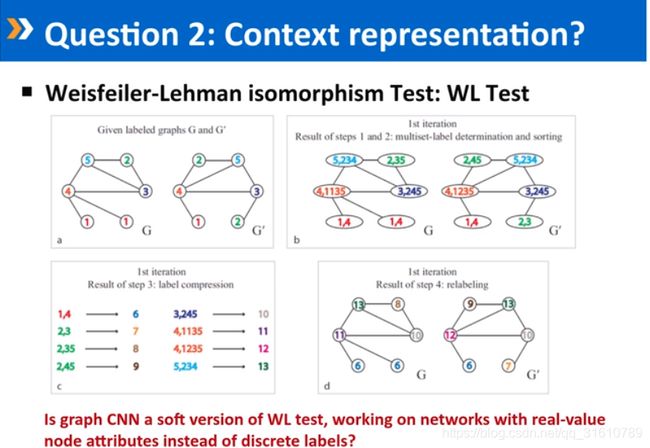
- 对于每一个节点,选择固定个数的节点进行,定义一个网络上邻近度的度量,可以使用W-L test的方式,或者其他方式进行选择
- 根据度量关系进行编号
- 参数共享
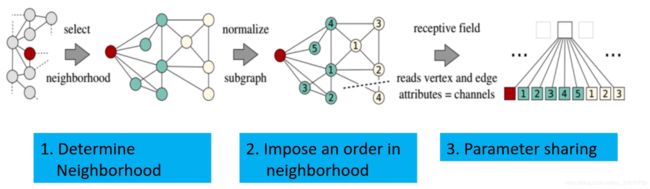
该使用的不多,很快出现其他想法,后来主要是用GCN和GAT等方法。
Inductive Respresentation Learning on Large Graphs. NeuralPS 2017
GraphSAGE
- 采用随机行走(restart type)的方式采样固定个数邻居节点,距离越近的节点,被选择的概率越大
a v ( k ) = A G G E R G A T E ( k ) ( h u ( k − 1 ) : u ∈ N ( v ) ) a_v^{(k)} = AGGERGATE^{(k)} (h_u^{(k-1)} :u \in {\mathcal{N}(v)} ) av(k)=AGGERGATE(k)(hu(k−1):u∈N(v)) - 聚合所选的邻居节点
h v ( k ) = C O M B I N E ( k ) ( h v ( k − 1 ) , a v ( k ) ) h_v^{(k)} = COMBINE^{(k)}( h_v^{(k-1)}, a_v^{(k)} ) hv(k)=COMBINE(k)(hv(k−1),av(k))
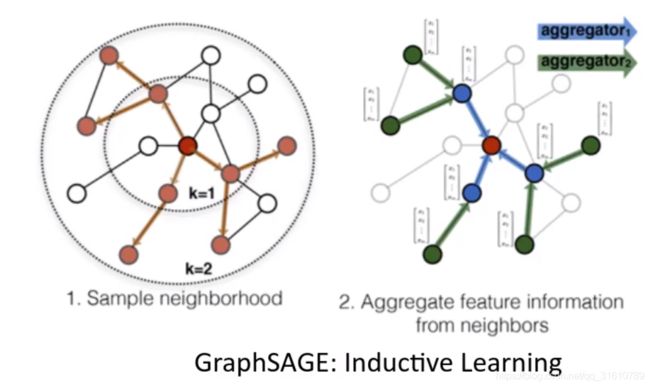
此时Graph卷积已经没有卷积的形式了,变成了GNN,已经没有图卷积的最初目标,而是一种Aggreagtion聚合过程。
使用聚合的方式,用这个节点的邻域节点的信息聚合后表达这个节点。
Semi-supervised classification with graph convolutional networks, ICLR2017
GCN(Graph Convolutional Network)
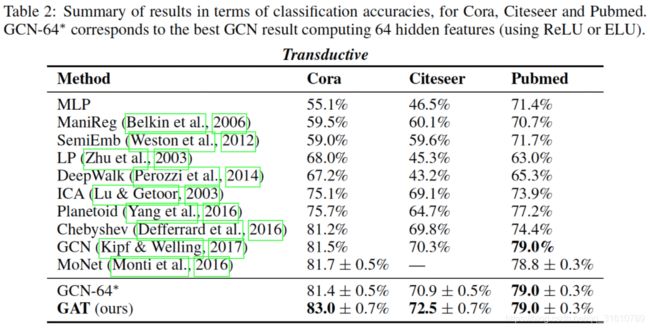
作者声明该方法是ChebyNet谱方法的简化版(其一阶近似),但也被认为是空间方法,并且把’GCN’这个名字给占了(占热搜)。
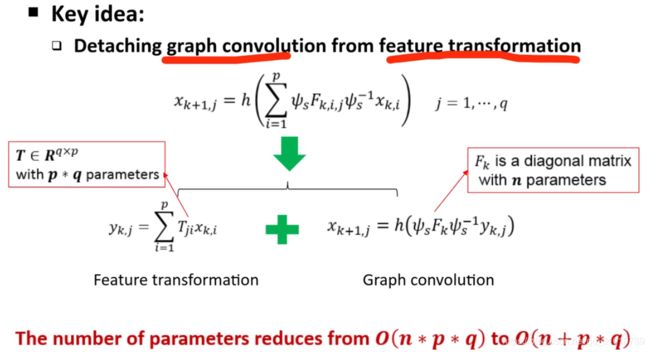
- 把目标节点的邻居节点进行聚合,将节点的特征变换之后进行加权平均,权重由Laplacian Matrix直接定义,非可变参数。不存在可学的卷积核,所以这里沈认为不能称之为卷积,更像是一种平滑操作/半监督学习。
- 共享参数来与特征变换
- ChebyNet谱方法的简化版(其一阶近似)
Z = f ( X , A ) = s o f t m a x ( A ^ R e L U ( A ^ X W ( 0 ) ) W ( 1 ) ) Z=f(X,A)=softmax(\hat{A}ReLU(\hat AXW^{(0)})W^{(1)}) Z=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))
其中 W ( 0 ) W^{(0)} W(0), W ( 1 ) W^{(1)} W(1) 是特征变换的参数
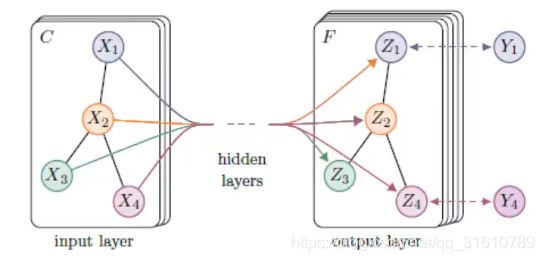
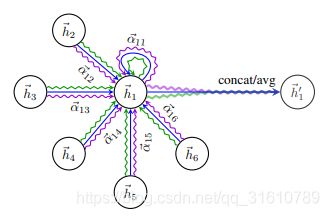
Graph Attention Network, ICLR2018
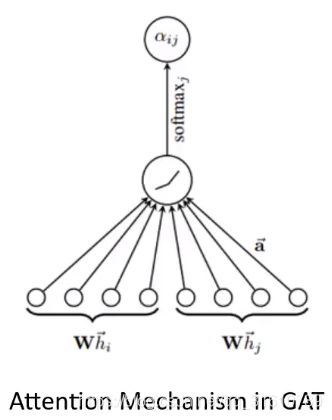
GAT(Graph Attention Network)(简写GAN已经被生成对抗网络占了…)
- 该作者认为GCN 只是学习聚合矩阵,参数传递依靠 Laplacian Matrix ,是 使用 W ( 0 ) W^{(0)} W(0), W ( 1 ) W^{(1)} W(1) 的特征变换,算不上卷积。
- 本文的参数共享来源于两个部分:
I. 特征变换
II. attition 的参数
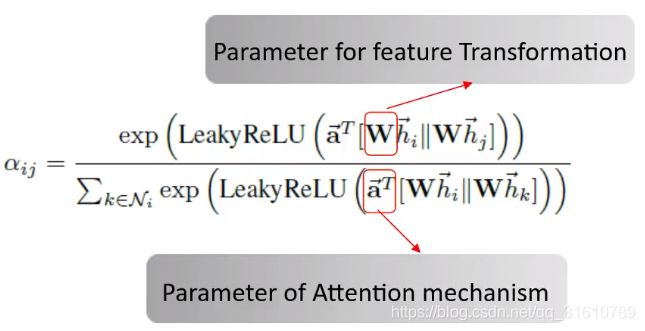
a ^ T \hat a^T a^T : 一个节点在聚合自己邻域节点时共享的参数,self-attition的参数
Geometric deep learning on graphs and manifolds using mixture model CNNs (2016)
MoNet: A general framework for spatial methods
- 定义一个图上的核函数,参数化或者非参数化都可,可以度量图上任意两个节点相似度。
- 卷积核就是这些核函数的权重
( f ∗ g ) ( x ) = ∑ j = 1 J g j D j ( x ) f (f*g)(x)=\sum_{j=1}^{J}g_jD_j(x)f (f∗g)(x)=j=1∑JgjDj(x)f
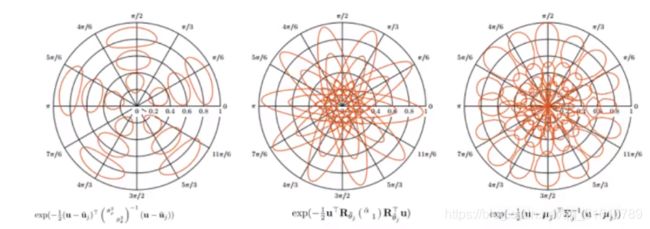
核函数:谱方法里就是普遍换的基,空间方法中就是要选的邻居节点的相似度表达
哪个定义更加深刻?
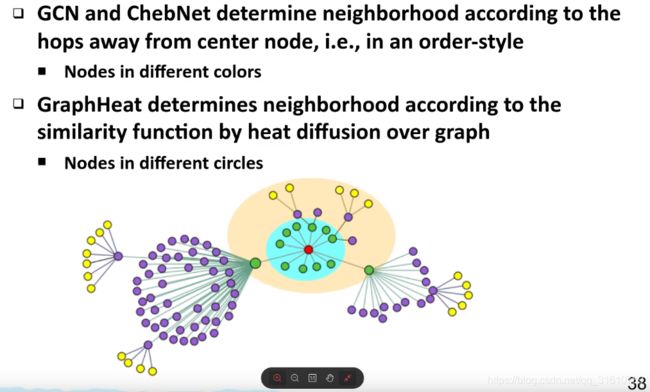
2019 IJCAI graph convolution networks using heat kernal for Semi-supervised Learning
沈自己的论文:
谱方法是空间方法的一个特例:
- 谱方法需要显式地定义卷积核,定义的时候我们已知将目标节点投影到了哪个空间(傅里叶变换:投影到L矩阵特征向量张开的空间,小波变换:小波基张开的空间)
2 . 空间方法不需要知道投影到了哪个空间,只需定义核函数和核矩阵
可以类比SVM,在SVM提出之前,都需要显式的做特征变换(基变换),SVM只需要定义一个核矩阵,空间未知。

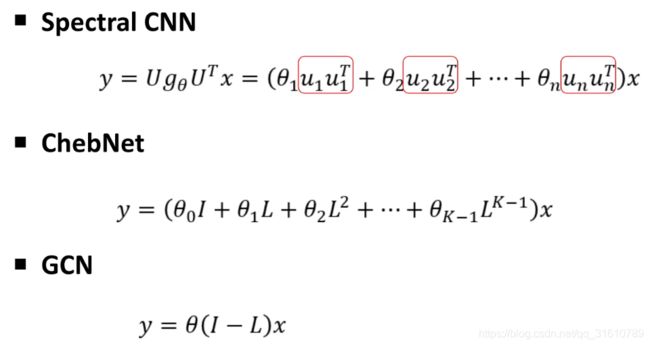
解释:都可以认为定义了不同的核矩阵与核参数
补:这里提出一个问题:为何GCN比ChebNet率高?
Graph signal processing: filter
对信号 x x x在某图上的平滑程度进行测量
对于节点分类任务,对特征平滑的要求是一致的。
Basic filters
- u i T L u i u_i^TLu_i uiTLui是一组基础滤波器
- 每一个滤波器 u i T L u i u_i^TLu_i uiTLui 仅让频率= λ i \lambda _i λi 的信号通过,图上的卷积操作是这组基础滤波器的线性组合。所以卷积又被称为过滤器。
x = α 1 u 1 + α 2 u 2 + . . . + α n u n x = \alpha_1 u_1+\alpha_2 u_2+...+\alpha_n u_n x=α1u1+α2u2+...+αnun
u i u i T x = α i u i u_iu_i^Tx=\alpha_i u_i uiuiTx=αiui
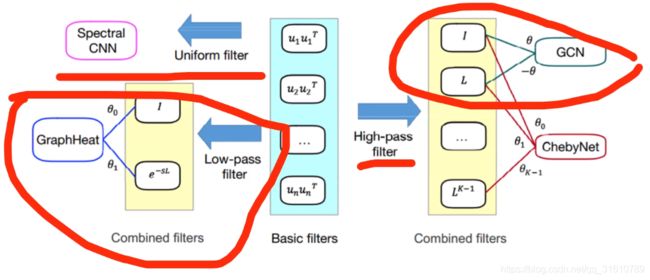
Combine filters
-
L k L^k Lk (ChebNet)是线性组合的特殊系数, { λ i k } i = 1 n \{\lambda_i^k\}_{i=1}^n {λik}i=1n
-
L k L^k Lk 决定频率越高的信号其权重越大,所以影响越大 ,是个高通滤波器。加强高频信号并不利于像分类任务。(认为是ChebNet不如GCN的原因)
GCN 只考虑k=0, k=1 的情况
- 过滤了高频信号
沈认为直接设计一个低通滤波器
低通滤波器
Compared with baseline methods
Neighborhood
Graph pooling
\
讨论
1
2. 上下文表示学习的体现
3. 未来应用
回答问题:
- 图上的高频信号有什么可以应用的?
图上的高频信号和做的任务有关:- 如果做的是节点分类的任务,它需要利用网络的平滑性,主要利用低频信号,
- 如果做得是异常节点检测,比如对于人造的graph或者iamge,想要区分出来是否为fake,这时候想要检测的异常信号通常是高频信号,因为人为很难将高频信号控制得精准。比如DeepFake的人脸生成。高频上会有很多震荡。
- 不同信号的小波基提取不同,如何定义?
沈等人使用指数衰减,其实就是刻画一个节点和周围邻域节点的影响关系。标准形式 e − L e^{-L} e−L (Laplacian Matrix的标准形式), 其实可以使用不同的函数形式: t a n ( x ) tan(x) tan(x) ,只要具有局部性就可以了。定义和常见的激活函数类似。 - 如何定义网络的相似性,如何寻找多个网络的子结构?
有人说称之为寻找网络的“词”,类似nlp里面的词。网络中比如:三角形、正方形等,用来实现图的迁移。上文中提到的匿名化的随机行走就是网络的结构,比如三角形就像“的”、“了”这类结构次,冗余的。
和应用领域相关,在生物领域,子结构更加具象化:一个CH2、苯环(C6H6)
和领域无关的有两种:- 叫WL的方式,带根的子图,
- 匿名化随机行走,Pathbase方法
- Motivebase
- 在Graph generation 方向有什么突出的研究和研究思路?
以前考虑的是:统计指标是否合适:度分布、三角形分布、小世界保持(注明的6人联系定律(非严谨)),像Scale Free Networks, 没听清、
现在已经在使用深度学习网络生成graph,在医药设计方面,比如给出一个新冠病毒,生成疫苗(很不成熟),更多的是特征分类,比如给出一类图(都是带硝基的),学习后生成这类图,目前还没啥生产领域。 - 为什么图神经网络学不到结构信息?
卷积设计有关,近两年有学者尝试将结构影响设计进去(Ego-discriminated GCN (EGCN)),但原来的GCN做邻居节点聚合的方式只是平滑,没有结构信息的体现,学习到的pattern是feature的各种组合方式。
近两年大家尝试如何把GCN做大做深,像CNN一样上千层。
目前整理到这,有写还没细化整理,抽空再整。