核密度聚类(一)核函数、核密度估计、核密度聚类
核密度聚类
当问题需要自动地确定聚类数目时,传统的KMeans等聚类方法不在适用。因此,使用“核概率密度估计”的思路自行设计了两种聚类方法。本文收录:
- 核是什么
- 核密度估计
- 基于核密度估计的两种聚类方法
- 代码实现
核函数
有一些数据,想“看看”它长什么样,基于高中的知识,我们一般会画频率分布直方图(Histogram)。但基于大学的知识,此时也可以用核密度估计,因为之前的知识水平让我们默认为频率等于概率,但实际情况不一定如此。
这里的“核”是一个函数,用来提供权重。例如高斯函数 (Gaussian) 就是一个常用的核函数。举个例子,假设我们现在想买房,钱不够要找亲戚朋友借,我们用一个数组来表示 5 个亲戚的财产状况: [8, 2, 5, 6, 4]。我们是中间这个数 5。“核”是一个权重函数,假设这个核函数的取值为[0.1, 0.4, 1, 0.3, 0.2],以此来代表同的亲戚朋友亲疏有别。
在借钱的时候,关系好的朋友出力多,关系不好的朋友出力少,于是我们可以用权重来表示。总共能借到的钱是: 8×0.1+2×0.4+5×1+6×0.3+4×0.2=9.2。
那么“核”的作用就是用来决定权重,例如高斯函数(即正态分布),呈现出距离中心越远,权重越小;反之,距离中心越近,权重越大的特点。核函数还有以下重要的性质:
- ∫−∞+∞K(x)dx=1
- K(−x)=K(x)
一些比较常用的核函数
均匀核函数 k(x)=1/2,-1≤x≤1 加入带宽h后: kh(x)=1/(2h),-h≤x≤h
三角 核函数 k(x)=1-|x|,-1≤x≤1 加入带宽h后: kh(x)=(h-|x|)/h^2,-h≤x≤h
伽马核函数 kxi(x)=[x^(α-1)exp{-xα/xi}]/[(xi/α)^α.Γ(α)]
高斯核函数K(x,xc)=exp(-||x-xc||^2/(2*σ)^2)其中xc为核函数中心,σ为函数的宽度参数。
核密度估计
由给定样本点集合求解随机变量的分布密度函数问题是概率统计学的基本问题之一。解决这一问题的方法包括参数估计和非参数估计。参数估计又可分为参数回归分析和参数判别分析。在参数回归分析中,人们假定数据分布符合某种特定的性态,如线性、可化线性或指数性态等,然后在目标函数族中寻找特定的解,即确定回归模型中的未知参数。在参数判别分析中,人们需要假定作为判别依据的、随机取值的数据样本在各个可能的类别中都服从特定的分布。经验和理论说明,参数模型的这种基本假定与实际的物理模型之间常常存在较大的差距,这些方法并非总能取得令人满意的结果。由于上述缺陷,Rosenblatt和Parzen提出了非参数估计方法,即核密度估计方法.由于核密度估计方法不利用有关数据分布的先验知识,对数据分布不附加任何假定,是一种从数据样本本身出发研究数据分布特征的方法,因而,在统计学理论和应用领域均受到高度的重视。
如果我们画频率分布直方图,其实目的是画出“概率密度函数”,因为统计直方图的组距无限接近于0时,得到的函数就是概率密度函数。
但直方图本质上是认为频率等于概率,但这种假设不是必然的。
核密度估计方法是一种非参数估计方法,非参数估计法指:如果一个估计问题所涉及的分布未知或不能用有穷参数来刻划,称这种估计为非参数估计。非参数估计是一种“平滑(smooth)”的手段:设 (x1,x2,⋯,xn) 是独立同分布的 n 个样本点,于是我们的估计:
p^(x)=1n∑i=1nKh(x−xi)=1nh∑i=1nK(x−xih)
上面式子中 x−xi 要提前归一化到 [−1,1] 之间。
这个公式的意思相当于是“我说的你可能不信,一起看看别人怎么说我的你就信了”。别人是指除自己外的其他样本点,距离越远的样本点权重越小,说话没有分量;距离样本点越近则权重越大,说话的可信度也就越高。当然权重的大小取决于实际采用的核函数,也可能距离越远权重越大,这里只是举个例子。
其中距离的远近通过x−xi的大小来衡量。相当于加权平均后,就能更好地了解我了,于是乎得到新的函数值作为这一点概率的取值。h 是人为指定的,代表“朋友圈”的大小,正式的叫法是“带宽”(bandwidth),且带宽越大曲线越平滑。
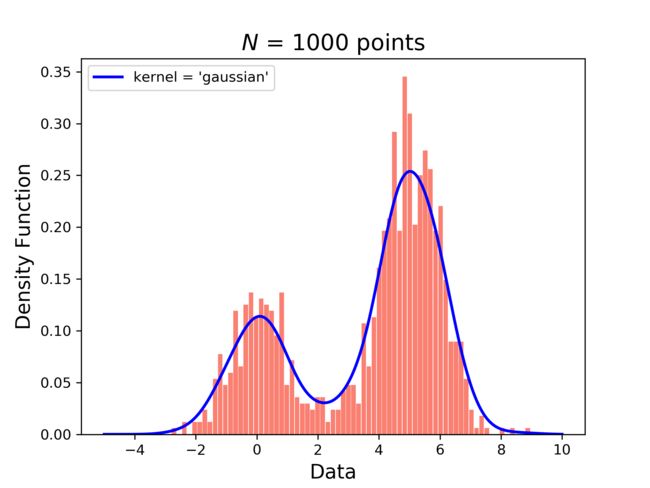
看一下核密度估计和频率分布直方图就能更好的理解了,蓝色的线为概率密度估计,橙色的柱状图为数据出现的频率统计。
核密度聚类
当然文章到这里还没有结束,要是到这里结束我就真成了抄袭文章的了。这组数据看上去很有聚类的趋势不是么,有两种聚类方法:
- 第一种方法。取曲线中的极大值和极小值分成几个区间,将数据的出现频率完成分类,此时会将出现频率相近的数据聚合在一起。按出现频率的高低分为四个居间A,B,C,D共四个类。则A类的数据出现频率最高,D类的数据出现频率最低。如下图所示:
- 第二种方法。既然曲线有多个极大值和极小值,那么何不以极大值极小值为分界点进行划分区间?按极值点的横坐标取值将数据分为四个居间A,B,C,D共四个类。那么此时对数据的含义也有了要求,即:每个数据段都有不同的含义,不能以数据出现的频率进行笼统划分。如下图所示:
 举个例子:图片的灰度值的取值范围是[0,255],假设[0,50]区间数据的出现频率和[200,255]区间数据的出现频率相近,但一定不能把这两组数据放在一起,因为前者代表黑色图层,后者代表白色图层。此时应以极大值、极小值等极值点的横坐标的取值划分区间,而后进行聚类更为合适。
举个例子:图片的灰度值的取值范围是[0,255],假设[0,50]区间数据的出现频率和[200,255]区间数据的出现频率相近,但一定不能把这两组数据放在一起,因为前者代表黑色图层,后者代表白色图层。此时应以极大值、极小值等极值点的横坐标的取值划分区间,而后进行聚类更为合适。 - 无论哪种方法,都能自动确定聚类数量。
核密度估计
本文着重实现第二种聚类方法,第一种其实同理。
首先产生一组随机数:
1 2 3 4 5 6 |
N = 1000 np.random.seed(1) # concatenate 用来组合两种数据,第一组数据均值0方差1,数量占 30% # 第二组数据均值 5 方差1 数量占 70% # [:, np.newaxis] 把数据维度更新为二维一列的数据 X = np.concatenate((np.random.normal(0, 1, int(0.3 * N)), np.random.normal(5, 1, int(0.7 * N))))[:, np.newaxis] |
其次调用sklearn这个库实现核密度估计即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
X_plot = np.linspace(-5, 10, 1000)[:, np.newaxis]
colors = ['blue']
kernels = ['gaussian']
lw = 2
for color, kernel in zip(colors, kernels):
# Fit the Kernel Density model on the data.
kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X)
# Evaluate the log density model on the data.
log_dens = kde.score_samples(X_plot)
plt.plot(X_plot[:, 0], np.exp(log_dens), color=color, lw=lw,
linestyle='-', label="kernel = '{0}'".format(kernel))
arr = np.exp(log_dens)
np.save('data.npy', arr)
|
- X_plot :An array of points to query;
- kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X) 完成训练工作,计算核密度;
- log_dens = kde.score_samples(X_plot) 评估这点的概率值该是多少。画图是连续的曲线,曲线上的点不一定在样本中,所以要弥补一些缺失的点;
- np.exp 是因为kde.score_samples反馈结果的概率值取了ln(可参看源码实现),所以计算真实概率值要exp一下;
- 保存数据用于后期聚类处理。
完整代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from scipy.stats import norm
N = 1000
np.random.seed(1)
X = np.concatenate((np.random.normal(0, 1, int(0.3 * N)), np.random.normal(5, 1, int(0.7 * N))))[:, np.newaxis]
X_plot = np.linspace(-5, 10, 1000)[:, np.newaxis]
colors = ['blue']
kernels = ['gaussian']
lw = 2
for color, kernel in zip(colors, kernels):
kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X)
log_dens = kde.score_samples(X_plot)
plt.plot(X_plot[:, 0], np.exp(log_dens), color=color, lw=lw,
linestyle='-', label="kernel = '{0}'".format(kernel))
arr = np.exp(log_dens)
np.save('data.npy', arr)
plt.legend(loc='upper left')
plt.hist(X, 70, normed = 1, histtype='bar', facecolor='salmon', rwidth=0.9)
# plt.set_xlim(-4, 9)
# plt.set_ylim(-0.02, 0.4)
plt.title("$N$ = 1000 points", fontsize=16)
plt.xlabel("Data", fontsize=14)
plt.ylabel("Density Function", fontsize=14)
plt.savefig('test.png', dpi=300)
|
求极值以聚类
之后借助scipy求出核密度估计的点中的几个极大值和极小值(极值并不唯一)
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np
from scipy.signal import argrelextrema
# 加载数据
data = np.load('data.npy')
# 求极大值
maxn = argrelextrema(data, np.greater)
# 求极小值
minn = argrelextrema(data, np.less)
# 打印极大值的索引
print(maxn)
# 打印极小值的索引
print(minn)
|
输出结果如下:
1 2 |
(array([340, 667], dtype=int64),) (array([480], dtype=int64),) |
得到的结果显示有两个极大值两个极小值,与概率密度估计图象相吻合。按照返回的极值索引访问极值即可。
1 |
print(data[minn]) |
进而按照极值划分数据,即可完成聚类。
转载自:核密度聚类 | Just for Life.