5--高斯混合聚类、学习向量量化算法 降维与度量学习

本周学习内容：

1. 继续学习高斯混合聚类、学习向量量化算法等聚类算法
2. 学习降维与度量学习部分的内容

1 聚类算法

1.1学习向量量化算法（LVQ learning vectorquantization）

   该算法试图找到一组原型向量来刻画聚类结构，LVQ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。该算法的学习流程如下：

  

  依旧使用西瓜数据集4.0，并假设第9-21号样本的类别标记为c2，其余数据类别标记为c1。这里是要找到q=5个原型向量来对数据进行聚类划分。具体代码如下所示：

for i in range(400):
    # 从样本集中随机选取一个样本
    j = random.randint(0, len(midu) - 1)
    dis = [np.linalg.norm(np.array([midu[j], hantanglv[j]]) - p[0]) for p in P]
    # 找出最近的原型向量
    minDis = dis.index(min(dis))
    # 更新原型向量
    if P[minDis][1] == mark[j]:
        p_ = P[minDis][0] + learningRate * (np.array([midu[j], hantanglv[j]]) - P[minDis][0])
    else:
        p_ = P[minDis][0] - learningRate * (np.array([midu[j], hantanglv[j]]) - P[minDis][0])
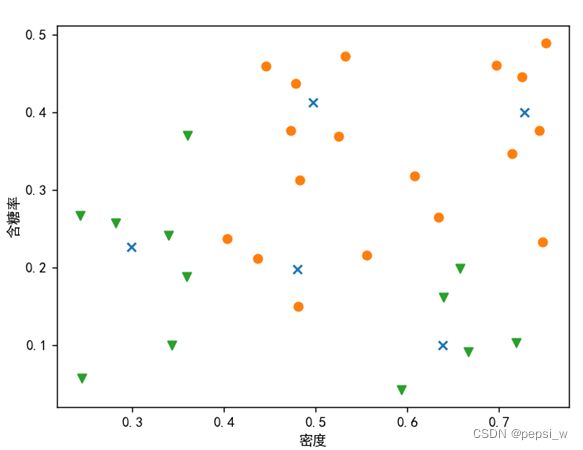
    P[minDis][0] = p_

  部分轮迭代后的结果如图1所示：

                                                          图1 LVQ算法迭代400轮后

1.2 高斯混合聚类（GMM Gaussian Mixture Model）

   从原型聚类的角度来看，高斯混合聚类时采用概率模型（高斯分布）对原型进行刻画，簇划分由原型对应后验概率确定。基本思想是用多个高斯分布函数去近似任意形状的概率分布，所以GMM就是由多个单高斯密度分布（Gaussi an）组成的，这些单高斯密度分布线性加和即为 GMM 的概率密度函数。

    该算法聚类过程：1）首先确定K值（模型的个数），并随机初始化每个簇的高斯分布参数。2）计算每个数据点属于每个高斯模型的概率。3）计算相应参数使得数据点的概率最大化，使用数据点概率的加权来计算新的参数，权重即为属于该簇的概率。4）重复迭代2和3直到收敛。

    依旧使用西瓜数据集4.0来进行k=3的聚类，其中通过EM算法对参数进行更新的代码如下：

# EM算法, 迭代更新 alpha
        for i in range(self.iter):
            gamma = computeGamma(data, miu, sigma, alpha, multiGaussian)
            alpha = np.sum(gamma, axis=0) / n_samples  # 纵向求和再除以样本数，即在每个聚类中，概率的平均值

            # 更新 miu
            for j in range(self.n_clusters):
                miu[j] = np.sum(data * gamma[:, j].reshape((n_samples, 1)), axis=0) / np.sum(gamma, axis=0)[j]
                sigma[j] = 0

                # 更新 sigma
                for k in range(n_samples):
                    sigma[j] += (data[k].reshape((1, n_features)) - miu[j]).T.dot(
                        (data[k] - miu[j]).reshape((1, n_features))) * gamma[k, j]
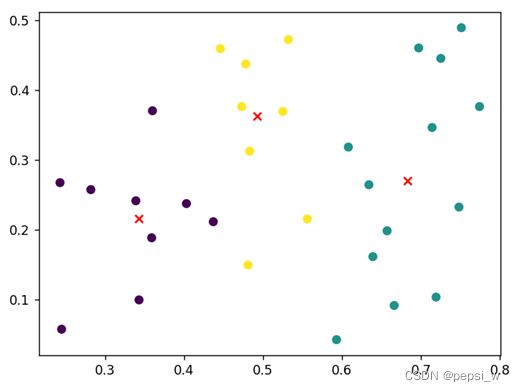
                sigma[j] = sigma[j] / np.sum(gamma, axis=0)[j]

    在迭代50轮后的聚类结果如图2所示，其中各高斯混合成分的均值向量用x来表示。

 

图2 高斯混合聚类50轮后的聚类结果

1.3 密度聚类（density-based clustering DBSCAN）

从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。DBSCAN 算法先根据给定的邻域参数(ϵ， MinPts) 找出所有核心对象，然后以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。

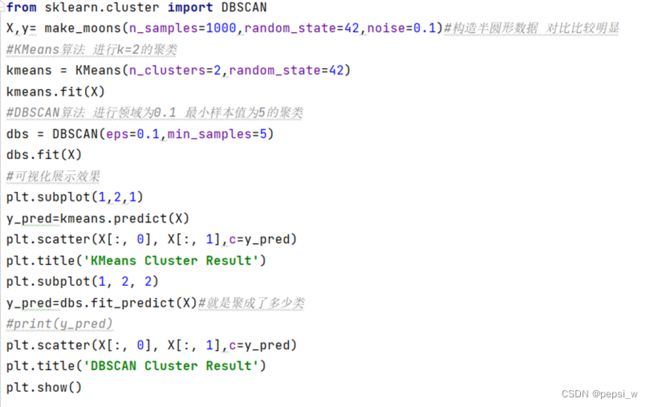
使用make_moons函数来构造半环形数据集，在该数据集上分别使用k-means算法和DBSCAN来对其进行聚类，具体代码如下所示：

 

将两种算法聚类结果如图3所示，可以看出在此类环形数据集上，基于密度聚类的DBSCAN算法聚类效果优于K-Means算法，且该算法不需要提前指定簇数 k就可以发现任意形状的聚类簇。从图3可以看出DBSCAN算法还标注出了数据集中的异常点，因此该算法可用于异常点检测。

 

图3 左边为K-Means算法（k=2）聚类结果 右边为DBSCAN算法聚类结果

1.4层次聚类（Hierarchical clustering）

层次聚类试图在不同层次对数据集进行划分，从而形成树形的聚类结构。其中AGENS是一种自底向上聚合策略的层次聚类算法，它先将数据集中的每一个样本看作一个初始聚类，然后在算法运行的每一步找出距离最近的两个簇进行合并，该过程不断重复，直至达到预设的聚类簇的个数。主要代码如下：

def AGNES(data, k, method):
    '''
    :param data: 数据
    :param k: 预设的聚类簇数
    :param method: 两个簇之间的距离公式
    :return: 分类好的簇
    '''
    cluster_num = len(data)
    C = []
    for i in data:  # 添加数据初始化
        tmp = [i]
        C.append(tmp)
    minDistList = getMinDistList(C, method)#获取最小距离列表
    while cluster_num > k:
        i, j, minDist = findMin(minDistList)#寻找距离最小的两个簇的信息 返回min_i, min_j, minDist
        C[i].extend(C[j])  # 合并
        del C[j]  # 删除
        minDistList = getMinDistList(C, method)
        cluster_num -= 1

    return C

其中两个簇之间的最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，平均距离则由两个簇所有样本共同决定。在西瓜数据集4.0上，选用不同的距离计算方式，设置k=4的聚类结果如图4所示，可以看出在该数据集上使用平均距离来划分的效果更好一些。

              图4 AGNES（k=4）算法使用不同距离计算公式在西瓜数据集上的划分结果

2 降维与度量学习

2.1 k近邻学习（K-Nearest Neighbor, KNN）

当对测试样本进行分类时，首先通过扫描训练样本集，找到与该测试样本最相似的k个训练样本，根据这个样本的类别进行投票确定测试样本的类别。也可以通过个样本与测试样本的相似程度进行加权投票。

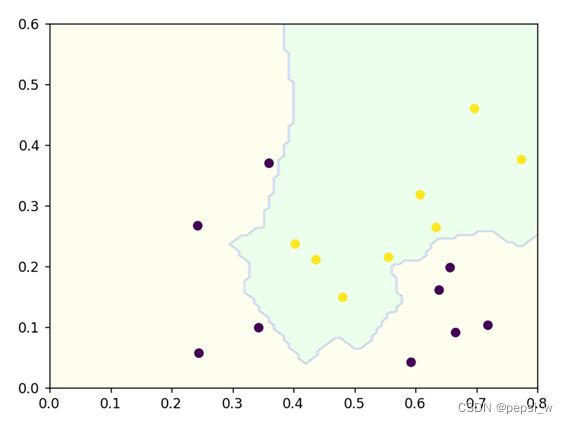
该算法在西瓜数据集3.0α上的分类边界如图5所示：

                                                   图5 k近邻分类器（k=3）的决策边界

2.2 降维方法

在高维情形下出现的数据样本稀疏、距离计算困难等问题，被称为维数灾难。缓解该问题的一个重要途径是降维，即通过某种数学变换将原始高维属性空间转变为一个低维子空间。在这个子空间中样本密度大幅提高，距离计算也更为容易。

1）多维缩放（MDS）算法

该算法要求原始空间中样本之间的距离在低维空间中得以保持。对该算法进行实现，运行结果如图6所示，虽然数据维数从3维降到了2维，但其样本呢空间的距离并没有改变。

                                                图6 MDS算法运行示例

2）主成成分分析（PCA）

  该算法通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

主要思想是将n维特征映射到k维上，这k维是全新的正交特征，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1，2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴。该算法的实现流程如图7所示：

图7 PCA算法

3）核化线性降维（KPCA）

PCA只能解决数据线性分部的情况，对于数据为非线性分部时则需把数据变成线性。这里同SVM一致引入核函数，将数据映射到高维空间使得其为线性分布，再使用PCA来解决。

4）流形学习（Isomap和LLE）

• Isomap

该算法与MDS本质上是一致的，只不过它考虑使用一个合适的距离度量 dij，使得该降维方法能够适用于流形的数据。当流形数据中的两个样本点有一定距离时，欧氏距离就不能很好地反映它们真实的距离远近。但是当两个样本的欧氏距离足够小的时候，这两个样本的真实情况一定也是比较接近的，即当距离足够小时，欧氏距离还是有效的。

对每个样本都选取它的 k 个最近的样本，将该样本与这 k 个邻居的欧氏距离，加入到原始的距离矩阵中。再计算任意两点间的距离，作为MDS算法的输入，使用MDS来对进行输出。

• LLE

局部线性，就是认为在整个数据集的某小范围内，数据是线性的。即每个样本点都能由它的邻域样本的坐标通过线性组合来得到。该算法首先用k近邻算法得到每个数据的k近邻点，再求这些近邻点的权重参数，并将这些关系映射到低维空间中。

下周计划：

1. 学习特征选择与稀疏学习部分内容
2. 学习计算学习理论

附：

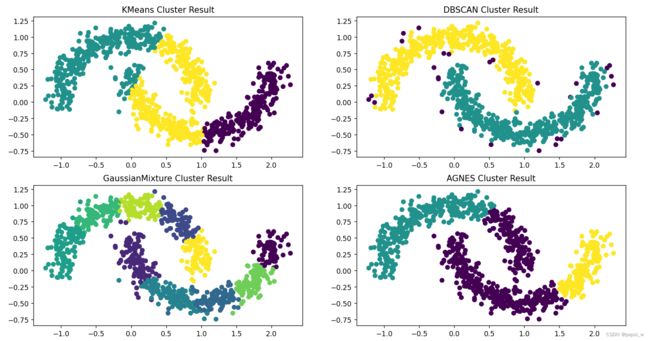
四种聚类算法在半圆形数据集上的表现

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from  sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
from sklearn.mixture import GaussianMixture
from sklearn.cluster import AgglomerativeClustering
X,y= make_moons(n_samples=1000,random_state=42,noise=0.1)#构造半圆形数据 对比比较明显
#X,y=make_blobs(n_samples=1500,cluster_std=[0.3,1.1,2.2],random_state=10)
#KMeans算法 进行k=2的聚类
kmeans = KMeans(n_clusters=3,random_state=42)
kmeans.fit(X)
#DBSCAN算法 进行领域为0.1 最小样本值为5的聚类
dbs = DBSCAN(eps=0.1,min_samples=5)
dbs.fit(X)
#高斯混合算法
gmm = GaussianMixture(n_components=10,random_state= 42)
gmm.fit(X)
#AGNES 层次聚类 k=3 使用平均距离计算
agg = AgglomerativeClustering(n_clusters= 3,linkage='ward')
agg.fit(X)
print("here")
#可视化展示效果
plt.subplot(2,2,1)
y_pred=kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1],c=y_pred)
plt.title('KMeans Cluster Result')

plt.subplot(2,2, 2)
y_pred=dbs.fit_predict(X)#就是聚成了多少类
#print(y_pred)
plt.scatter(X[:, 0], X[:, 1],c=y_pred)
plt.title('DBSCAN Cluster Result')

plt.subplot(2, 2, 3)
y_pred=gmm.fit_predict(X)#就是聚成了多少类
#print(y_pred)
plt.scatter(X[:, 0], X[:, 1],c=y_pred)
plt.title('GaussianMixture Cluster Result')

plt.subplot(2, 2, 4)
y_pred=agg.fit_predict(X)#就是聚成了多少类
#print(y_pred)
plt.scatter(X[:, 0], X[:, 1],c=y_pred)
plt.title('AGNES Cluster Result')
plt.show()

 运行结果：