聚类分析——客户分群分析

聚类分析——客户分群分析

一、聚类
聚类分析主要是针对无监督问题，即没有标签值。回顾之前python分析淘宝用户行为（三），我们再运用RFM模型时，人为制作评分系统，并打上标签值，今天主要是直接将其当作无监督问题来处理
简单来说，就是将相似的东西分到一组，比如说我们进行客户分群时，会根据其价值进行分群，从而制定精准策略。但聚类也存在一些问题，比如说如何评估，如何调参等等。
二、K-Means算法
理论解释并不是很难理解，我简单说一下自己的理解，现在有很多组数据，没有标签值，只能根据他们之间的相似度进行分组。
**过程：**指定需要分多少种客户类型，即K值，然后选取质心（利用向量各维取平均值），选完后将周围的点计算欧几里得距离，最后根据距离进行相似分类。

**优势：**简单，快速，适合常规数据集

**劣势：**K值难确定；复杂度与样本呈线性关系；很难发现任意形状的簇
三、DBSCAN算法
1、基本概念

**核心对象：**若某个点的密度达到算法设定的阈值则其为核心点（即r领域内的数量不小于minPts）

**\epsilon-领域的距离阈值：**设定的半径r
**直接密度可达：**若某点p在点q的领域内，且q是核心点则p-q直接密度可达

**密度可达：**若有一个点的序列q0,q1…qk，对于任意其qi-qi-1是直接密度可达的，则称为从q0到qk密度可达，这实际上是直接密度可达的“传播”

**过程：**数据集-指定半径（r）-密度阈值（Minpts）-进行聚类
参数选择：

**半径：**可以根据K距离来设定

**K距离：**给定数据集P ={p(i)；i=0,1,…n},计算点p(i)到集合D的子集S中所有点的距离，距离按照从小到大的顺序排序，d(K)就被称为k-距离

**MinPts：**k-距离中k的值，一般取的小一些，多次尝试

**优势：**不需要指定簇个数;可以发现任意形状的簇;擅长找到离群点（检测任务）;两个参数就够了。
**劣势：**高维数据有些困难（可以做降维）;参数难以选择（参数对结果的影响非常大）;sklearn中效率很慢（数据削减策略）。

四、练习

本次分析数据来源CDNow网站的用户在1997年1月1日至1998年6月30日期间内购买CD交易明细。数据集一共有用户ID，购买日期，订单数，订单金额四个字段。对其利用RFM模型进行聚类分析。

第一步：获取数据，并进行简单的数据清洗

import pandas as pd
import numpy as np
columns=['user_id','order_time','order_products','order_money']
data=pd.read_table(r'C:\Users\Administrator\Desktop\python\project\聚类分析\RFM\CDNOW.txt',sep='\s+',names=columns)
data.head()
print(data.describe())
print(data.info())
# 查看异常值
missing = data.isnull().sum()
# 删除重复值
data = data.drop_duplicates(keep ='first',inplace = False)
# 检查异常值，并删掉（本数据中，订单金额为0，是异常数据）
expect = data[data['order_money']==0] 
data=data.drop(index=(data.loc[(data['order_money']==0)].index)) 
# 数据类型转换，注意看到日期数据，基本都是下面操作
data['order_time'] = pd.to_datetime(data['order_time'],format = '%Y%m%d')

第二步，构造特征向量
关于RFM模型进行客户分组时，需要R、F、M值，以下为构造过程：

# R值是最近一次消费时间与截至时间的间隔（用day来衡量）
data['order_interval']= pd.to_datetime('1998-06-30')-data['order_time']
data['order_interval'] = data['order_interval'].apply(lambda x:x.days) #去掉日期间隔的days
# F值是指消费的频率，M值表示消费的金额
rfm = data.groupby(['user_id'],as_index = False).agg({'order_interval':'min','order_products':'count','order_money':'sum'})
rfm.columns = ['user_id','r','f','m']  #重命名列：最近一次订单r，订单频率f和订单总金额m

第三步，进行模型建立之前，需要对数据进行标准化处理

from sklearn.preprocessing import StandardScaler
data = StandardScaler().fit_transform(rfm.loc[:,['r','f','m']])
第四步：建立模型
from sklearn.cluster import KMeans
kmodel = KMeans(n_clusters=3)
kmodel.fit(data)

# 查看聚类结果
kmeans_cc = kmodel.cluster_centers_  # 聚类中心
print('各类聚类中心为：\n',kmeans_cc)
kmeans_labels = kmodel.labels_  # 样本的类别标签
print('各样本的类别标签为：\n',kmeans_labels)
r1 = pd.Series(kmodel.labels_).value_counts()  # 统计不同类别样本的数目
print('最终每个类别的数目为：\n',r1)

各类聚类中心为：
 [[ 0.62263953 -0.33099376 -0.26103463]
 [-1.37152564  0.60113127  0.42723658]
 [-1.77096075  7.04810188  7.79356919]]
各样本的类别标签为：
 [0 0 1 ... 0 0 0]
最终每个类别的数目为：
 0    16182
1     7170
2      150
dtype: int64

# 输出聚类分群的结果
cluster_center = pd.DataFrame(kmodel.cluster_centers_,columns = ['ZR','ZF','ZM'])   # 将聚类中心放在数据框中
cluster_center.index = pd.DataFrame(kmodel.labels_ ).drop_duplicates().iloc[:,0]  # 将样本类别作为数据框索引
print(cluster_center)

     ZR        ZF        ZM
0                              
0  0.622640 -0.330994 -0.261035
1 -1.371526  0.601131  0.427237
2 -1.770961  7.048102  7.793569

简单的聚类分析就是这样，根据结果，我们发现这些客户被分为了三种，其中第0组的占比非常大，应该是最近购买间隔占比较大，说明公司的可持续性高。第1组购买频率较高，说明客户粘性较大，最后一组的购买频率和购买金额都较高，可以进行VIP服务。
将结果进行可视化分析，从而更清晰的进行结果分析。

# 客户分群雷达图
labels = ['ZR','ZF','ZM']
legen = [' customers' + str(i + 1) for i in cluster_center.index]  # 客户群命名，作为雷达图的图例
lstype = ['-',':','-.']
kinds = list(cluster_center.iloc[:, 0])
# 由于雷达图要保证数据闭合，因此再添加L列，并转换为 np.ndarray
cluster_center = pd.concat([cluster_center, cluster_center[['ZR']]], axis=1)
centers = np.array(cluster_center.iloc[:, 0:])

# 分割圆周长，并让其闭合
n = len(labels)
angle = np.linspace(0, 2 * np.pi, n, endpoint=False)
angle = np.concatenate((angle, [angle[0]]))

import matplotlib.pyplot as plt
# 绘图
fig = plt.figure(figsize = (8,6))
ax = fig.add_subplot(111, polar=True)  # 以极坐标的形式绘制图形
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 画线
for i in range(len(kinds)):
    ax.plot(angle, centers[i], linestyle=lstype[i], linewidth=3, label=kinds[i])
# 添加属性标签
ax.set_thetagrids(angle * 180 / np.pi, labels)
plt.title('Customer Profile Analysis')
plt.legend(legen)

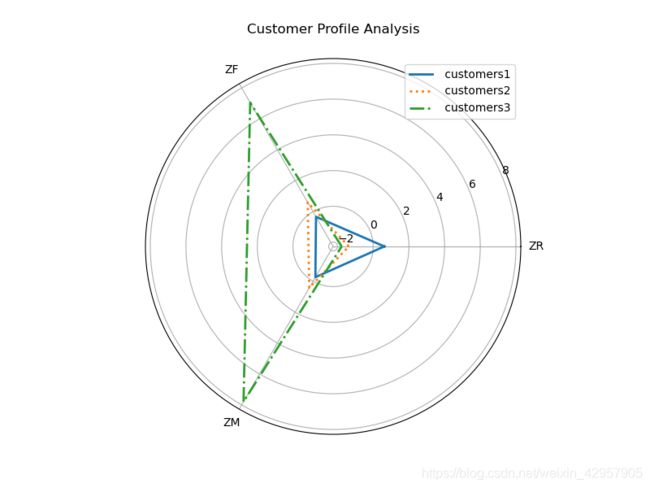
当然，看上面这个图，我们发现分类分得并不是很好，我们可以利用肘部法和轮廓系数来进行相应的评估和调参。

from sklearn.metrics import silhouette_score,silhouette_samples
for n_clusters in range(2,10):
    km = KMeans(n_clusters=n_clusters)
    preds = km.fit_predict(data)
    centers =km.cluster_centers_
    score = silhouette_score(data,preds)
    print('For n_clusters = {},silhouette_score is {}'.format(n_clusters,score))
# 寻找轮廓系数接近1的，在这个情况下，还是k=3，轮廓系数最高

综上所述，聚类分析用在无监督问题，具体问题还是要具体分析，这个案例只是练习，也可以将特征进行一系列处理，从而达到更好的效果。