【机器学习】(十九)聚类:k均值聚类、凝聚聚类、DBSCAN,算法评估
聚类:将数据划分成组的任务。这些组叫簇。
k均值聚类(KMeans)
迭代算法:将每个数据点分配给最近的簇中心->簇中心修改为所分配点的平均值->循环前两步,直至簇中心不再变化。
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import KMeans
# two_moons数据集
x, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据聚类为4个簇
kmeans = KMeans(n_clusters=4, random_state=0)
kmeans.fit(x) # 为x中的每个训练数据点分配一个簇标签
print("x_labels:\n{}".format(kmeans.labels_)) # 存储标签信息的属性 = kmeans.predict(x)
y_pred = kmeans.predict(x)
# 绘制数据点
plt.scatter(x[:, 0], x[:, 1], c=y_pred, cmap='Paired')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=60,
marker='^', c=range(kmeans.n_clusters), linewidths=2, cmap='Paired')
KMeans类对象的,labels_属性保存训练得到的簇标签,cluster_centers_属性保存簇中心。n_clusters参数设置簇的数目。

k均值假设所有的簇在某种程度上具有相同的“直径”,还假设所有方向对每个簇都同等重要。(月牙数据集即使分两个簇,也不会一个月牙一个簇)
矢量量化观点:k均值可以看作一种分解方法,每个点用单一分量来表示。单一分量由簇中心给出。
分解方法PCA或者NMF只能通过降维来分类,这个数据集只有二维,使用PCA或NMF会破坏数据的结构。k均值做矢量量化,可以用比输入维数更多的簇来对数据进行编码。
优点:相对容易理解和实现;运行速度相对较快;可以轻松扩展到大型数据集
缺点:依赖于随机初始化;对簇形状的假设和约束性较强;需要指定所需要的簇的个数。
凝聚聚类(AgglomerativeClustering)
凝聚聚类指的是许多基于相同原则构建的聚类算法。
迭代算法:每个点是自己的簇(一个点一个簇)->合并有链接准侧度量的最相似的簇->满足停止准则(簇的个数)就不在合并。
scikit-learn提供的三种链接准则:
| 选项 | 说明 |
|---|---|
| ward | 默认选项。挑选两个簇,使得所有簇的方差增加最小 |
| average | 将簇中所有点之间平均距离最小的两个簇合并 |
| complete | (最大链接)将簇中点之间最大距离最小的两个簇合并 |
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs
x, y = make_blobs(random_state=1)
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(x)
mglearn.discrete_scatter(x[:, 0], x[:, 1], assignment)
聚类算法不能对新数据点做出预测,没有predict方法,可以用fit_predict方法。需要指定n_clusters参数。

缺点:凝聚聚类仍然无法分离想two_moons数据集这样复杂的形状。
DBSCAN
具有噪声的基于密度的空间聚类应用(DBSCAN)。不需要设定簇的个数;可以划分具有复杂形状的簇;可以扩展到较大的数据集。缺点是速度较慢。
DBSCAN原理是识别特征空间的“拥挤”区域中的点(在一坨的点是一个簇)。具有两个参数,min_samples参数(表示相邻点的最少数量,默认2)参数和eps参数(表示相邻范围距离,可以隐式控制簇的个数,默认0.5)。
迭代算法:随机选择一个点->找到这个点距离小于等于eps的所有点->点的个数小于min_samples,标记为噪声;否则为核心样本/核心点,分配一个簇标签->噪声抛弃,重新寻找一个随机点;核心点范围内的邻居,叫边界点,为没有簇标签的邻居分配簇标签->如果边界点是核心点,再次发散访问其邻居。->范围内再无核心点,重新选择一个未访问的点,重复。
DBSCAN不能对新数据点做出预测,使用fit_predict方法。边界点所属的簇依赖于数据点的访问顺序。
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
x, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 缩放数据
scaler = StandardScaler()
scaler.fit(x)
x_scaled = scaler.transform(x)
dbscan = DBSCAN(eps=0.2)
clusters = dbscan.fit_predict(x)
plt.scatter(x_scaled[:, 0], x_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
聚类算法评估
用真实值评估聚类
用一些指标(调整rand指数(ARI)、归一化信息(NMI))可以用于评估聚类算法相对于真实聚类的结果。用0(不相关的聚类)-1(最佳)度量,ARI可以是负值。
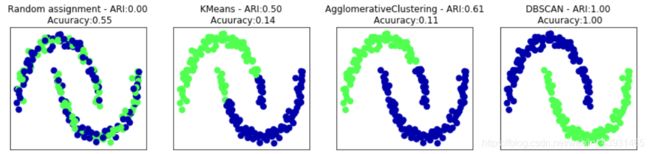
用ARI比较三种聚类方法
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
import mglearn
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
# 创建数据并将数据缩放
x, y = make_moons(n_samples=200, noise=0.05, random_state=0)
x_scaled = StandardScaler().fit_transform(x)
fig, axes = plt.subplots(1, 4, figsize=(15,3), subplot_kw={'xticks':(), 'yticks':()})
# 列出聚类算法
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2), DBSCAN()]
# 创建一个随机的簇分配
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(x))
# 绘制随机分配
axes[0].scatter(x[:,0], x[:,1], c=random_clusters, cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment - ARI:{:.2f}\n Acuuracy:{:.2f}".format(adjusted_rand_score(y, random_clusters),
accuracy_score(y, random_clusters)))
# 绘制簇分配
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(x_scaled)
ax.scatter(x_scaled[:,0], x_scaled[:,1], c=clusters, cmap=mglearn.cm3, s=60)
ax.set_title("{} - ARI:{:.2f}\n Acuuracy:{:.2f}".format
(algorithm.__class__.__name__, adjusted_rand_score(y, clusters), accuracy_score(y, clusters)))
| 评估函数 | 说明 |
|---|---|
| adjusted_rand_score() | 评价哪些点位于同一个簇中,簇标签不重要 |
| accuracy_score() | 要求分配的簇标签与真实值完全匹配 |
在没有真实值的情况下评估聚类
在应用聚类算法是,通常没有真实值来比较结果。一些聚类的评分指标(轮廓系数)不需要真实值。
轮廓系数计算一个簇的紧致度,其值越大越好,最高分为1。不允许复杂形状。
from sklearn.metrics.cluster import silhouette_score
from sklearn.metrics.cluster import silhouette_score
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
import mglearn
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
# 创建数据并将数据缩放
x, y = make_moons(n_samples=200, noise=0.05, random_state=0)
x_scaled = StandardScaler().fit_transform(x)
fig, axes = plt.subplots(1, 4, figsize=(15,3), subplot_kw={'xticks':(), 'yticks':()})
# 列出聚类算法
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2), DBSCAN()]
# 创建一个随机的簇分配
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(x))
# 绘制随机分配
axes[0].scatter(x[:,0], x[:,1], c=random_clusters, cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment:{:.2f}".format(silhouette_score(x_scaled, random_clusters)))
# 绘制簇分配
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(x_scaled)
ax.scatter(x_scaled[:,0], x_scaled[:,1], c=clusters, cmap=mglearn.cm3, s=60)
ax.set_title("{}:{:.2f}".format(algorithm.__class__.__name__, silhouette_score(x_scaled, clusters)))