SLAM 几何基础
SLAM 几何基础
- 1. 向量运算及其几何意义
-
- 1.1 内积
-
- 1.1.1 内积定义
- 1.1.2 内积几何意义
- 1.1.3 内积微分性质
- 1.2 外积
-
- 1.2.1 外积定义
- 1.2.2 外积几何意义
- 1.2.3 外积微分性质
- 2. 线面特征运算
-
- 2.1 点到直线距离
- 2.2 点到平面距离
Reference:
- 深蓝学院-多传感器融合
1. 向量运算及其几何意义
1.1 内积
1.1.1 内积定义
内积,又叫数量积,是向量的点乘。
a = ( x 1 , y 1 , z 1 ) , b = ( x 2 , y 2 , z 2 ) a ⋅ b = x 1 x 2 + y 1 y 2 + z 1 z 2 \mathbf{a}=(x_1, y_1, z_1),\quad \mathbf{b}=(x_2, y_2, z_2) \\ \mathbf{a} \cdot\mathbf{b} = x_1x_2+y_1y_2+z_1z_2 a=(x1,y1,z1),b=(x2,y2,z2)a⋅b=x1x2+y1y2+z1z2
1.1.2 内积几何意义
当 b \mathbf{b} b为单位向量时,内积就是 a \mathbf{a} a在 b \mathbf{b} b上的投影分量。
a ⋅ b = ∣ a ∣ ∣ b ∣ c o s θ \mathbf{a} \cdot\mathbf{b} = |\mathbf{a}| |\mathbf{b}|cos\theta a⋅b=∣a∣∣b∣cosθ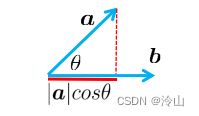
1.1.3 内积微分性质
从内积的定义出发,有:
∂ a ∙ b ∂ a = b \frac{\partial \boldsymbol{a} \bullet \boldsymbol{b}}{\partial \boldsymbol{a}}=\boldsymbol{b} ∂a∂a∙b=b证明:
∂ a ∙ b ∂ x 1 = ∂ ( x 1 x 2 + y 1 y 2 + z 1 z 2 ) ∂ x 1 = x 2 ∂ a ∙ b ∂ y 1 = ∂ ( x 1 x 2 + y 1 y 2 + z 1 z 2 ) ∂ y 1 = y 2 ∂ a ∙ b ∂ z 1 = ∂ ( x 1 x 2 + y 1 y 2 + z 1 z 2 ) ∂ z 1 = z 2 \begin{aligned} & \frac{\partial \boldsymbol{a} \bullet \boldsymbol{b}}{\partial x_1}=\frac{\partial\left(x_1 x_2+y_1 y_2+z_1 z_2\right)}{\partial x_1}=x_2 \\ & \frac{\partial \boldsymbol{a} \bullet \boldsymbol{b}}{\partial y_1}=\frac{\partial\left(x_1 x_2+y_1 y_2+z_1 z_2\right)}{\partial y_1}=y_2 \\ & \frac{\partial \boldsymbol{a} \bullet \boldsymbol{b}}{\partial z_1}=\frac{\partial\left(x_1 x_2+y_1 y_2+z_1 z_2\right)}{\partial z_1}=z_2 \end{aligned} ∂x1∂a∙b=∂x1∂(x1x2+y1y2+z1z2)=x2∂y1∂a∙b=∂y1∂(x1x2+y1y2+z1z2)=y2∂z1∂a∙b=∂z1∂(x1x2+y1y2+z1z2)=z2
1.2 外积
1.2.1 外积定义
外积,又叫叉积、向量积,是向量的叉乘。
a = ( x 1 , y 1 , z 1 ) b = ( x 2 , y 2 , z 2 ) a × b = ∣ i j k x 1 y 1 z 1 x 2 y 2 z 2 ∣ = ( y 1 z 2 − y 2 z 1 ) i − ( x 1 z 2 − x 2 z 1 ) j + ( x 1 y 2 − x 2 y 1 ) k \begin{aligned} &\boldsymbol{a}= \left(x_1, y_1, z_1\right) \\ &\boldsymbol{b}= \left(x_2, y_2, z_2\right) \\ & \boldsymbol{a} \times \boldsymbol{b} = \left|\begin{array}{ccc} \mathrm{i} & \mathrm{j} & \mathrm{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{array}\right| = \left(y_1 z_2-y_2 z_1\right) i -\left(x_1 z_2-x_2 z_1\right) j +\left(x_1 y_2-x_2 y_1\right) k \end{aligned} a=(x1,y1,z1)b=(x2,y2,z2)a×b= ix1x2jy1y2kz1z2 =(y1z2−y2z1)i−(x1z2−x2z1)j+(x1y2−x2y1)k
1.2.2 外积几何意义
外积模长等于 a \mathbf{a} a和 b \mathbf{b} b组成的平行四边形的面积,外积的方向满足右手定则, a \mathbf{a} a和 b \mathbf{b} b张成平面的单位法向量为: n = a × b ∣ a × b ∣ \mathbf{n}=\frac{\mathbf{a} \times \mathbf{b}}{|\mathbf{a} \times \mathbf{b} |} n=∣a×b∣a×b。
a × b = ∣ a ∣ ∣ b ∣ s i n θ \mathbf{a} \times \mathbf{b} = |\mathbf{a}| |\mathbf{b}|sin\theta a×b=∣a∣∣b∣sinθ
1.2.3 外积微分性质
根据外积的定义,有:
a × b = a ∧ b \boldsymbol{a} \times \boldsymbol{b}=\boldsymbol{a}^{\wedge} \boldsymbol{b} a×b=a∧b其中 a ∧ a^{\wedge} a∧ 为 a a a 的反对称矩阵:
a ∧ = [ 0 − z 1 y 1 z 1 0 − x 1 − y 1 x 1 0 ] \boldsymbol{a}^{\wedge}=\left[\begin{array}{ccc} 0 & -z_1 & y_1 \\ z_1 & 0 & -x_1 \\ -y_1 & x_1 & 0 \end{array}\right] a∧= 0z1−y1−z10x1y1−x10 则:
a ∧ b = − b ∧ a ∂ a ∧ b ∂ a = − b ∧ ∂ a ∂ a = − b ∧ \begin{aligned} \boldsymbol{a}^{\wedge} \boldsymbol{b} & =-\boldsymbol{b}^{\wedge} \boldsymbol{a} \\ \frac{\partial \boldsymbol{a}^{\wedge} b}{\partial a} & =-\frac{b^{\wedge} \partial a}{\partial a}=-\boldsymbol{b}^{\wedge} \end{aligned} a∧b∂a∂a∧b=−b∧a=−∂ab∧∂a=−b∧
2. 线面特征运算
2.1 点到直线距离
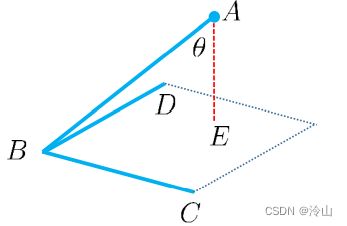
点 A A A 到直线 B C BC BC 的距离为: ∣ A D → ∣ = ∣ A B → × A C → ∣ ∣ B C → ∣ |\overrightarrow{A D}|=\frac{|\overrightarrow{A B} \times \overrightarrow{A C}|}{|\overrightarrow{B C}|} ∣AD∣=∣BC∣∣AB×AC∣,即平行四边形面积除以对角线长度。

2.2 点到平面距离
平面 B C D B C D BCD 的单位法向量为 n = B C → × B D → ∣ B C → × B D → ∣ \boldsymbol{n}=\frac{\overrightarrow{B C} \times \overrightarrow{B D}}{|\overrightarrow{B C} \times \overrightarrow{B D}|} n=∣BC×BD∣BC×BD 点 A A A 到平面 B C D B C D BCD 的距离为:
∣ A E → ∣ = ∣ A B → ∣ cos θ = A B → ∙ n |\overrightarrow{A E}|=|\overrightarrow{A B}| \cos \theta=\overrightarrow{A B} \bullet \boldsymbol{n} ∣AE∣=∣AB∣cosθ=AB∙n(即先计算单位向量给出方向,再使用点乘计算距离)