【算法】机器人走迷宫（适用于走迷宫、最短路径算法）-20200412

标题：机器人走迷宫（适用于走迷宫、最短路径算法）
问题描述：

1. 一块矩形方格，含有障碍和可通行格子，求从某一点到另外一点的最短距离？N*M的矩阵；
   其中，1代表障碍，0代表可通行；示例：给定二维矩阵
   0 0 1 0
   0 1 0 0
   0 0 0 0
   0 0 0 0

出发点坐标[0, 0],终点坐标[2, 3];
java编写int solve(int[][] grids, int[] start, int[] end)返回最短距离；

思路：
（1）机器人在矩阵范围内可以向上下左右走；
（2）终点[2, 3]可以由[2,1]或[1, 3]走来；可在起点到点[2,1]的距离、起点到[1, 3]的距离中取最小值，再加1（格子之间距离为1）即可；
（3）对于算法初学者，自然想到递归；
当然，递归肯定可以解决问题，但是必须要不能找下去再递归回来，太慢了；时间复杂度O(N^2);
(4)另外一种方式呢？从起点给你1步，你能走到起点的上下左右（当上下左右在格子中）；扩散1步后，再扩散1步。。。是否可以扩散到终点，这个距离就是最短距离；就像气味扩散一样，

半径是最短距离。能扩散到终点即可，不必求出终点四周的点，再取min值；----算法效率最高；时间复杂度O（N）；

2.若要打印最短路径呢？在历史信息中拉出来，已在代码中注释；

3.若机器人有一次清理障碍的机会呢？代码如何写？–下回分解

4.附带经典带权图最短路径的BFS代码；与方格不同的是，带权需要考虑比较权值大小；

Solution.java:
package robot;

import java.util.*;

public class Solution {
int[][] direct = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

// 方格的dfs
public int dfs(int[][] grids, int[] start, int[] end, Set> passedPaths) {
    // 每次递归要new flagPaths, 不然会重用导致程序不正确，切很难定位；兵家大忌；
    Set> tmpSet = new HashSet<>(passedPaths);
    tmpSet.add(Arrays.asList(start[0], start[1]));
    if ((Math.abs(start[0] - end[0]) == 0 && Math.abs(start[1] - end[1]) == 1)
            || (Math.abs(start[0] - end[0]) == 1 && Math.abs(start[1] - end[1]) == 0)) {
        return 1;
    }
    int minLen = 1000;
    for (int[] item : direct) {
        int nextX = start[0] + item[0];
        int nextY = start[1] + item[1];
        if (nextX >= 0
                && nextX <= grids.length - 1
                && nextY >= 0
                && nextY <= grids[0].length - 1
                && grids[nextX][nextY] != 1
                && !tmpSet.contains(Arrays.asList(nextX, nextY))
                ) {
            // 满足要求才能递归：1、坐标在格子中；2、格子不是障碍；3、不能来回走，从某个点走出来的，不能遍历四个方向造成走回去；
            int len = dfs(grids, new int[]{nextX, nextY}, end, tmpSet);
            System.out.printf("start to end:%d, %d; %d, %d. -- %d.\n", nextX, nextY, end[0], end[1], len);
            minLen = Math.min(len, minLen);
        }
    }
    return minLen + 1;
}

// 方格的bfs;
public int bfs(int[][] grids, int[] start, int[] end) {
// 写是否已经访问的状态；
int[][] state = new int[grids.length][grids[0].length];
Queue queue = new LinkedList();
// 注意：若要打印最短路径，必须将历史信息塞入队列；
queue.offer(start);
state[start[0]][start[1]] = 1;
int count = 0;
while (!queue.isEmpty()) {
count++;
int size = queue.size();
for (int inx = 0; inx < size; inx++) {
int[] node = (int[]) queue.poll();
// 当扩散到终点就拉出来；注意：若要打印最短路径，到达终点时可以拉出来；
if (node[0] == end[0] && node[1] == end[1]) {
// 起点塞进来已经加1，故要减去；
return count - 1;
}
for (int[] item : direct) {
int nextX = node[0] + item[0];
int nextY = node[1] + item[1];
if (nextX >= 0 && nextX <= grids.length - 1
&& nextY >= 0 && nextY <= grids[0].length - 1
&& grids[nextX][nextY] != 1 && state[nextX][nextY] != 1) {
queue.offer(new int[]{nextX, nextY});
state[nextX][nextY] = 1;
}
}
}
}
return -1;
}

public int getMinLen(Map> relMap, Map, Integer> valueMap) {
    Map pathMap = new HashMap<>();
    pathMap.put("a", 0);
    Queue queue = new LinkedList();
    queue.offer("a");
    while (!queue.isEmpty()) {
        String curNode = (String) queue.poll();
        if (curNode.equals("e")){
            break;
        }
        for (String subNode : relMap.get(curNode)) {
            List key = Arrays.asList(curNode, subNode);
            if (null == pathMap.get(subNode)) {
                pathMap.put(subNode, pathMap.get(curNode) + valueMap.get(key));
            } else {
                Integer len = pathMap.get(subNode);
                pathMap.put(subNode, Math.min(len, pathMap.get(curNode) + valueMap.get(key)));
            }
            queue.offer(subNode);
        }
    }
    return pathMap.get("e");
}

}

Main.java
import robot.Solution;

import java.util.*;

public class Main {
public static void main(String[] args){
int[][] grids = {
{0, 0, 1, 0},
{0, 1, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0}
};
int[] start = {0, 0};
int[] end = {2, 3};
Set flag = new HashSet<>();
System.out.println(new Solution().dfs(grids, start, end, flag));
System.out.println(new Solution().bfs(grids, start, end));

    /**
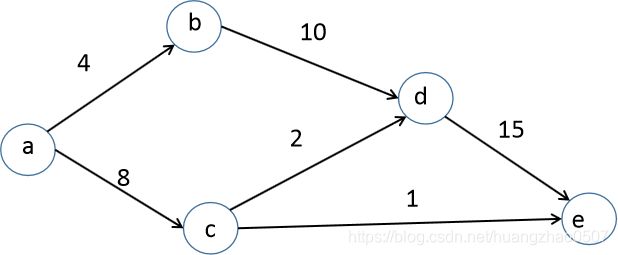
     * 图：
     * a -> b  权值：4
     * a -> c  权值：8
     * b -> d  权值：10
     * c -> d  权值：2
     * c -> e  权值：1
     * d -> e  权值：15
     */
    // 也可以自己用邻接矩阵；
    Map> relMap = new HashMap<>();
    relMap.put("a", Arrays.asList("b", "c"));
    relMap.put("b", Arrays.asList("d"));
    relMap.put("c", Arrays.asList("d", "e"));
    relMap.put("d", Arrays.asList("e"));

    Map, Integer> valueMap = new HashMap<>();
    valueMap.put(Arrays.asList("a", "b"), 4);
    valueMap.put(Arrays.asList("a", "c"), 8);
    valueMap.put(Arrays.asList("b", "d"), 10);
    valueMap.put(Arrays.asList("c", "d"), 2);
    valueMap.put(Arrays.asList("c", "e"), 1);
    valueMap.put(Arrays.asList("d", "e"), 15);

    System.out.println(new Solution().getMinLen(relMap, valueMap));
}

}

结果：
5
5
9