概率统计公式大赏

概率论

概念	公式
样本点	随机试验的每一种可能的结果，记作ω
样本空间	全体样本点组成的集合，记作Ω，是必然事件
空集	不包含任何样本点的空集，记作∅，是不可能事件
随机事件	样本空间的子集，记作A,B,C⋯
基本事件	由一个样本点组成的样本空间的子集
事件的包含	一个事件的发生必然导致另一个事件发生，或者一个事件的样本点都属于另一个事件
相等事件	两个事件具有完全相同的样本点
相交事件	代表事件A和事件B同时发生的事件，记作AB或A∩B
互斥事件	AB=∅的两个事件，也叫互不相容事件
互斥概率	两两互斥的事件有P(A1∪A2∪⋯∪An)=P(A1)+P(A2)+⋯+P(An)
事件并集	代表事件A和事件B至少有一个发生的事件，记作A+B或A∪B
对立事件	记作A’，A+A’=Ω，AA’=∅
完备事件组	一组两两互斥，但全部并起来可以组成样本空间的事件
事件的差	包含于A而不包含于B的事件称为A与B的差，记作A-B或AB’
事件的交换律	A+B=B+A，AB=BA
事件的结合律	(A+B)+C=A+(B+C)，(AB)C=A(BC)
事件的分配律	A(B+C)=AB+AC，A+BC=(A+B)(A+C)
事件的对偶律	(A+B)’=A’B’，(AB)’=A’+B’，(A-B)’=(AB’)’=A’+B
条件概率	事件A发生时事件B发生的概率P(B|A)=$\begin{array}{c}\underline{P(AB)}\\ P(A)\end{array}$
概率性质	P∅=0，P(Ω)=1，P(A)∈[0,1]，P(A’)=1-P(A)，A⊆B⇒P(A)≤P(B)
古典概率	P(A)=$\begin{array}{c}\underline{A中样本点的数量}\\ \Omega 中样本点的总数\end{array}=\begin{array}{c}\underline{n(A)}\\ n(\Omega )\end{array}$
几何概率	P(A)=$\begin{array}{c}\underline{A的几何度量}\\ \Omega 的几何度量\end{array}=\begin{array}{c}\underline{L(A)}\\ L(\Omega )\end{array}$
概率加法	P(A+B)=P(A)+P(B)-P(AB)
概率减法	P(A-B)=P(A)-P(AB)
概率乘法	P(AB)=P(A)P(B│A)=P(B)P(A│B)
全概率公式	P(A)=∑P(Bi)P(A│Bi)，B为非零完备事件组
贝叶斯公式	P(Bk│A)=$\begin{array}{c}\underline{P(A{B}_k)}\\ P(A)\end{array}=\begin{array}{c}\underline{P(B_k)P(A│B_k)}\\ \sum P(B_i)P(A│B_i)\end{array}$，B为非零完备事件组
独立与相关	独立⇔P(AB)=P(A)P(B)或f{X,Y}(x,y)=fX(x)fY(y)⇒不相关⇔E(XY)=E(X)E(Y)
独立事件特性	多个事件相互独立⇒P(ABC)=P(A)P(B)P(C)，它们中的部分事件相互独立
独立重复试验	重复若干次的随机试验，每次实验之间相互独立，且同一事件在每次实验中发生的概率相同，比如掷骰子
伯努利试验	每次实验只有A，A’两种结果的独立重复试验，比如抛硬币
n重伯努利试验	重复n次的伯努利实验
排列与组合	$A_n^m=\begin{array}{c}n!\\ \overline{(n-m)!}\end{array}，C_n^m=\begin{array}{c}n!\\ \overline{m!(n-m)!}\end{array}$
分布函数	FX(x) = P(X ≤ x)=${\int }_{-\infty }^x$fX(x)dx；FX(-∞)=0，FX(+∞)=1；在间断点处 FX(x)=FX(x+)
因变量分布函数	Y=g(X)⇒ FY(y)=P(Y ≤ y)=P(g(X) ≤ y)
概率密度	fX(x)=F’X(x)，P(a${\int }_a^b$fX(x)dx，${\int }_{-\infty }^{+\infty }$fX(x)dx=1
离散型变量分布	P(X=xi)=pi或$\frac{\begin{array}{cccc}X│x_1& x_2& \cdots & x_n\end{array}}{\begin{array}{cccc}P│p_1& p_2& \cdots & p_n\end{array}}$，∑pi=1
0-1分布	若P(X=0)=1-p，P(X=1)=p，0
二项概率	若每次试验中P(A)=p∈(0,1)，则n重伯努利实验中A发生k次的概率=Cnkpk(1-p)n-k
二项分布B	若P(X=k)=Cnkpk(1-p)n-k，k∈N，p∈(0,1)，则X~B(n,p),E(X)=np,D(X)=np(1-p)
二项分布可加性	X~B(m,p)，Y~B(n,p)⇒X+Y~B(m+n,p)
几何分布	若P(X=k)=p(1-p)k-1，k∈N+，p∈(0,1)，则X服从参数为p的几何分布，E(X)=$\frac{1}{p}$，D(X)=$\frac{1}{p^2}-\frac{1}{p}$
超几何分布	若P(X=k)=$\frac{\begin{array}{c}{C}_M^k{C}_{N-M}^{n-k}\end{array}}{\begin{array}{c}{C}_N^n\end{array}}$，k∈[max(0,n+M-N),min(n,M)]，则X~H(n,M,N)
超几何分布的意义	N件产品中有M件次品，从中抽取n件，样本中含k个次品
泊松分布P	若P(X=k)=$\frac{{\lambda }^k{e}^{-\lambda }}{k!}$，λ>0，k∈N，则X~P(λ)，E(X)=D(X)=λ
泊松分布可加性	X~P(λ1)，Y~P(λ2)⇒X+Y~P(λ1+λ2)
均匀分布U	若f(x)=$\{\begin{array}{c}\begin{array}{c}1\\ \overline{b-a}\end{array},a<x<b\\ 0,其它\end{array}$，则X~U(a,b)，E(X)=$\begin{array}{c}\underline{a+b}\\ 2\end{array}$，D(X)=$\begin{array}{c}\underline{(a-b{)}^2}\\ 12\end{array}$
指数分布E	若f(x)=$\{\begin{array}{c}\lambda e^{-\lambda x},x>0\\ 0,其它\end{array}$，λ>0，则X~E(λ)，E(X)=λ-1，D(X)=λ-2
正态分布N	若f(x)=$\begin{array}{c}1\\ \overline{\sqrt{2\pi }\sigma }\end{array}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$，σ>0，则X~N(μ,σ2)，E(X)=μ，D(X)=σ2
标准正态分布	X~N(0,1)，Φ(x)=$\begin{array}{c}1\\ \overline{\sqrt{2\pi }}\end{array}{\int }_{-\infty }^x{e}^{-\frac{x^2}{2}}\mathrm{d}x$，Φ’(x)=φ(x)=$\begin{array}{c}1\\ \overline{\sqrt{2\pi }}\end{array}{e}^{-\frac{x^2}{2}}$
正态分布特性1	X~N(μ,σ2) ⇒ aX+b~N(aμ+b,(aσ)2)，$\frac{X-\mu }{\sigma }$~N(0,1)
正态分布特性2	X~N(μ,σ^2) ⇒ F(X)=Φ($\begin{array}{c}\underline{X-\mu }\\ \sigma \end{array}$)，P(a$\begin{array}{c}\underline{b-\mu }\\ \sigma \end{array}$)-Φ($\begin{array}{c}\underline{a-\mu }\\ \sigma \end{array})$
二维随机变量	若X,Y是样本空间上的两个随机变量，则(X,Y)为二维随机变量
二维离散随机变量	可能取有限个或可数无穷个值的二维随机变量
二维离散变量分布	P(X=xi,Y=yj)=pij，∑pij=1
二维连续变量分布	F(x,y)=P(X≤x,Y≤y)=${\int }_{-\infty }^x{\int }_{-\infty }^y$f(x,y)dydx
二维分布的性质1	F(x,-∞)=F(-∞,y)=0，F(+∞,+∞)=1，在单个维度上单调不减且“右连续”
二维分布的性质2	P(aDf(x,y)dydx
边缘分布	fX(x)=${\int }_{-\infty }^{+\infty }$f(x,y)dy，FX(x)=${\int }_{-\infty }^x{\int }_{-\infty }^{+\infty }$f(x,y)dydx，${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }$f(x,y)dydx=1
条件分布	F{X|Y}(x|y)=P(X≤x|Y=y)
条件密度	f{X|Y}(x|y)=$\begin{array}{c}\underline{f(x,y)}\\ f_Y(y)\end{array}$
二维正态分布	(X,Y) ~ N(μ1,μ2,σ12,σ22,ρxy)，f=$\begin{array}{c}1\\ \overline{2\pi {\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}\end{array}\exp [-\begin{array}{c}\underline{(\frac{x-{\mu }_1}{{\sigma }_1}{)}^2-2\rho (\frac{x-{\mu }_1}{{\sigma }_1})(\frac{y-{\mu }_2}{{\sigma }_2})+(\frac{y-{\mu }_2}{{\sigma }_2}{)}^2}\\ 2(1-{\rho }^2)\end{array}]$
多维正态分布特性1	(X1,X2,⋯,Xn)服从多维正态分布⇔Xi服从正态分布，X1,X2,⋯,Xn的线性组合服从正态分布
多维正态分布特性2	(X1,X2,⋯,Xn)服从多维正态分布⇒X1,X2,⋯,Xn相互独立且两两不相关
二元函数的分布	Z=f(X,Y)⇒FZ(z)=P(Z≤z)=P(f(X,Y)≤z)
数学期望/样本均值	E(g(X))=∑pig(xi)=${\int }_{-\infty }^{+\infty }$g(x)fX(x)dx，E(C)=C，E(aX+bY)=aE(X)+bE(Y)，$\bar{X}=\frac{1}{n}\sum X_i$
二元数学期望	E(Z)=E[g(X,Y)]=∑pijg(xi,yj)=${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }$f(x,y)g(x,y)dydx
方差/标准差	D(X)=σ2(X)=E([X-E(X)]2)=E(X2)-E2(X)，$S^2=\begin{array}{c}\underline{\sum (X_i-\bar{X}{)}^2}\\ n-1\end{array}$，σ或S为标准差
方差特性	D(aX+b)=a2D(X)，D(X±Y)=D(X)+D(Y)±2Cov(X,Y)
样本的矩	k阶原点矩$=\frac{1}{n}\sum X_i^k$，k阶中心矩$=\frac{1}{n}\sum (X_i-\bar{X}{)}^k$
二级中心矩展开	$\frac{1}{n}\sum (X_i-\bar{X}{)}^2=\overline{X^2}-{\bar{X}}^2$
混合矩	(k+l)阶混合矩=E(XkYl)，(k+l)阶混合中心矩=E([X-E(X)]k[Y-E(Y)]l)
协方差	Cov(X,Y)=E([X-E(X)][Y-E(Y)])=E(XY)-E(X)E(Y)
协方差的性质	Cov(X,Y)=Cov(Y,X)，Cov(aX,bY)=abCov(X,Y)，Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
协方差矩阵	在协方差矩阵C中，cij=Cov(Xi,Xj)
相关系数	ρxy=$\begin{array}{c}Cov(X,Y)\\ \overline{\sqrt{D(X)\cdot D(Y)}}\end{array}$∈[-1,1]，为1(-1)时线性正（负）相关，为0时不相关
均值之均值	E($\bar{X}$)=E(X)=μ
均值之方差	D($\bar{X}$)=$\frac{1}{n}$D(X)=$\begin{array}{c}\underline{{\sigma }^2}\\ n\end{array}$
方差之均值	E(S2)=D(X)=σ2
方差之方差1	Xi~N(μ,σ2) ⇒ ∑$(\begin{array}{c}\underline{X_i-\mu }\\ \sigma \end{array}{)}^2$~χ²(n) ⇒ D[$(\begin{array}{c}\underline{X_i-\mu }\\ \sigma \end{array}{)}^2$]=2n ⇒ D[∑(Xi-μ)2]=2nσ4
方差之方差2	Xi~N(μ,σ2) ⇒ $\begin{array}{c}\underline{n-1}\\ {\sigma }^2\end{array}$S2∼χ²(n-1) ⇒ D[$\begin{array}{c}\underline{n-1}\\ {\sigma }^2\end{array}$S2]=2(n-1) ⇒ D(S2)=$\begin{array}{c}2{\sigma }^4\\ \overline{n-1}\end{array}$
依概率收敛	∃随机变量X1,X2,⋯,Xn，∀ε>0，$\underset{n\to \infty }{\lim }$P(|Xn-C|<ε)=1⇒Xi依概率收敛于常数C，记作Xn$\stackrel{P}{\to }$C
依概率收敛的特性	$X_n\stackrel{P}{\to }a,Y_n\stackrel{P}{\to }b\Rightarrow X_n\pm Y_n\stackrel{P}{\to }a\pm b,X_n{Y}_n\stackrel{P}{\to }ab,\begin{array}{c}\underline{X_n}\\ Y_n\end{array}\stackrel{P}{\to }\begin{array}{c}\underline{a}\\ b\end{array},g(X_n)\stackrel{P}{\to }g(a)$
大数定律	∃随机变量X1,X2,⋯,Xn，$\bar{X}=\frac{1}{n}\sum X_i,\bar{X}\stackrel{P}{\to }E(\bar{X})$⇒随机变量序列{Xn}服从大数定律，棣-拉中的Xn可换成∑Xi
常用大数定律

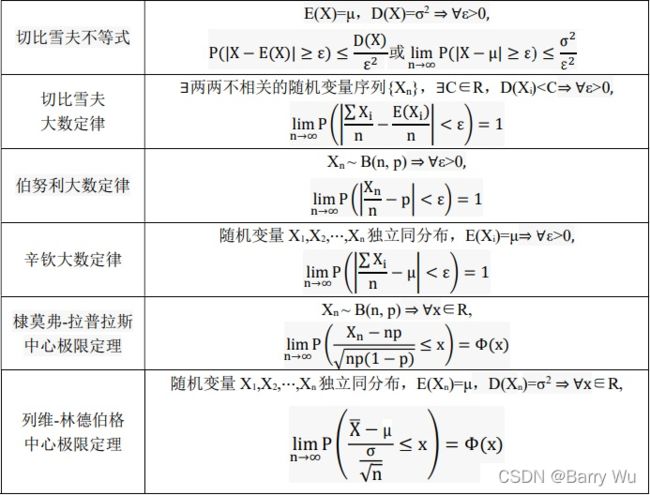数理统计

概念	公式
总体	所研究对象的某项指标X的全体
简单随机样本	来自总体的，相互独立且与总体同分布的随机变量
样本容量	样本的随机变量的个数n
样本值	总体X的n个独立观测值X1,X2,⋯,Xn
统计量	样本X1,X2,⋯,Xn的不含未知参数的函数T=T(X1,X2,⋯,Xn)
点估计	用样本X1,X2,⋯,Xn构造的统计量$\hat{\theta }$(X1,X2,⋯,Xn)估计未知参数$\theta$的过程
估计量/估计值	X1,X2,⋯,Xn为点估计的统计量，x1,x2,⋯,xn为估计量所取得的观测值
矩估计	用样本矩估计各阶总体矩：E(X)=$\frac{1}{n}$∑Xi，E(X2)=$\frac{1}{n}$∑Xi2，⋯，从而解出各参数，某一阶方程解不出就解高一阶方程
似然函数	L(θ)=L(X1,X2,⋯,Xn)=∏f(xi)或∏p(Xi)，连续型为概率密度之积，离散型为各样本对应概率之积
最大似然估计	令$\begin{array}{c}\underline{\partial \ln L(\theta )}\\ \partial {\theta }_i\end{array}=0$并解出使L(θ)最大的参数$\hat{\theta }$，解不出就让L尽可能大，比如$\hat{\theta }$=max(Xi)
无偏估计量	θ的无偏估计量$\hat{\theta }$满足$E(\hat{\theta })=\theta$
渐进无偏估计量	θ的渐进无偏估计量$\hat{\theta }$满足$\underset{n\to \infty }{\lim }[E(\hat{\theta })-\theta ]=0$
更有效估计量	设${\hat{\theta }}_1$和${\hat{\theta }}_2$都是θ的无偏估计量，若$D({\hat{\theta }}_1)\le D({\hat{\theta }}_2)$，则${\hat{\theta }}_1$比${\hat{\theta }}_2$更有效
最有效估计量	∀i，$D({\hat{\theta }}_0)\le D({\hat{\theta }}_i)\Rightarrow {\hat{\theta }}_0$是θ的最有效估计量
一致估计量	设$\hat{\theta }=\hat{\theta }$(X1,X2,⋯,Xn)是θ的估计量，如果$\hat{\theta }$依概率收敛于θ，则$\hat{\theta }$是θ一致估计量
相合/一致估计量1	设${\hat{\theta }}_n=\hat{\theta }$(X1,X2,⋯,Xn)是θ的估计量，∀ε>0，$\underset{n\to \infty }{\lim }P(│{\hat{\theta }}_n-\theta │<\epsilon )=1\Rightarrow {\hat{\theta }}_n$是θ的相合估计量
相合/一致估计量2	设$\hat{\theta }=\hat{\theta }$(X1,X2,⋯,Xn)是θ的估计量，∀ε>0，$\underset{n\to \infty }{\lim }P(│\hat{\theta }-\theta │<\epsilon )=1\Rightarrow {\hat{\theta }}_n$是θ的相合估计量
分位点	满足${\int }_{-\infty }^{f_a}$f(x)dx=a的fa
χ²分布	X1,X2,⋯,Xn相互独立，Xi~N(0,1)⇒χ²=∑Xi2~χ²(n)
χ²分布的性质	E(χ²)=n，D(χ²)=2n；χ²1和χ²2相互独立，χ²1~χ²(a)，χ²2~χ2(b)⇒χ²1+χ²2 ~ χ²(a+b)
t分布	X~N(0,1)，Y~χ²(n)⇒T=$\begin{array}{c}X\\ \overline{\sqrt{\frac{Y}{n}}}\end{array}$~t(n)
t分布的性质	t分布的概率密度是偶函数，$\underset{n\to \infty }{\lim }$T~N(0,1)
F分布	X,Y相互独立，X~χ²(a)，Y~χ²(b)⇒F=$\begin{array}{c}\begin{array}{c}\underline{X}\\ a\end{array}\\ \overline{\begin{array}{c}\underline{Y}\\ b\end{array}}\end{array}$~F(a,b)
F分布的性质	F~F(a,b)⇒$\frac{1}{F}$~F(b,a)
显著度/置信度	显著性水平=a=接近0的数，置信度=1-a=接近1的数
联方差	$S_w^2=\begin{array}{c}\underline{(n_1-1)S_1^2+(n_2-1)S_2^2}\\ n_1+n_2-2\end{array}$
置信区间
假设检验	按照一定的规则根据样本判断所作假设的真伪，并接受或拒绝该假设。如果对总体所作的假设为真，那么不利于该假设的小概率事件在一次试验中几乎不可能发生；如果小概率事件发生，就有理由怀疑该假设的真实性，从而拒绝原假设
假设检验过程	根据样本观察结果检验原假设，接受原假设（H0）则否定备择假设（H1），否定H0就则接受H1
两端/一端检验	H0:μ=μ0,H1:μ≠μ0；H0:μ≥μ0,H1:μ<μ0或H0:μ≤μ0,H1:μ>μ0
第一类错误	拒绝实际真实的H0，也叫“弃真”，P(弃真)=P(拒绝域|H0)
第二类错误	接受实际不真的H0，也叫“纳伪”，P(纳伪)=P(接受域|H1)
一正态总体验μ	H0:μ=μ0，接受域为$u=\left|\begin{array}{c}\underline{\bar{X}-{\mu }_0}\\ \frac{\sigma }{\sqrt{n}}\end{array}\right|<u_{1-a/2}$，P(弃真)=a；全8种接受域和置信区间同样
一正总单侧验μ	H0:μ≤μ0的接受域为ua，以此类推