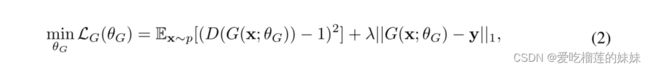026利用GANs合成癫痫脑活动2019

Synthetic Epileptic Brain Activities using GANs

摘要：

癫痫是一种慢性神经系统疾病，影响着全世界6500多万人，表现为反复无故发作。目前正在开发监测脑电图(EEG)信号的现代系统，目的是检测癫痫发作，以提醒护理人员并减少癫痫发作对患者生活质量的影响。这类系统使用机器学习算法，需要大量标记的癫痫发作数据进行训练。然而，对医学专家和患者来说，获取癫痫发作的脑电图信号是一个昂贵和耗时的过程。在这项工作中，我们生成了合成的类似癫痫发作的脑电图信号，该信号可用于训练癫痫发作检测算法，减少了对记录数据的需求。首先，我们用30名癫痫患者的数据训练生成对抗网络(GAN)。然后，我们为新的、看不见的患者生成合成训练集，总体上产生与真实数据训练集相当的检测性能。我们使用EPILEPSIAE Project的数据集来演示我们的结果，癫痫检测是世界上最大的公共数据库之一。

在这项工作中，我们提出了使用GAN来产生高质量的合成癫痫发作脑电图(EEG)信号，可用于训练检测算法并实现最先进的结果。

2 生成模型

我们的模型是一个条件GAN，在给定输入端非发作(发作间期)脑电图样本的情况下，生成癫痫发作(发作)的脑电图样本。我们设计的基本原理是，虽然癫痫发作的记录非常昂贵，但间期信号可以很容易地记录。因此，我们根据目标患者的癫痫发作间期样本对网络进行调整，以便向生成器提供额外的信息，以便利用这些信息生成更真实的癫痫发作样本。通过这种方式，我们可以使用已经存在的数据库来训练GAN，然后使用GAN为新患者生成癫痫发作样本。

我们的模型的生成器是一个U-net卷积自编码器网络，具有加权跳过连接，其中解码器将潜在代码转换为动态样本。为了在模型中引入随机性，将均值为0，标准差为1的高斯噪声级联到潜码中。跳跃连接将编码器每一层的特征映射与训练中学习到的权重相乘，然后将该操作的结果添加到解码器相应的特征映射中。我们的GAN鉴别器与生成器的编码器结构相同，但它在输出端包含一个额外的全连接层。我们的GAN的损失函数基于最小二乘GAN (LSGAN) 。因此，鉴别器的最小化目标由下式给出:

其中函数D对应于鉴别器，G对应于发生器和。输入数据 x 从输入数据分布p中采样，θD为鉴别器的网络参数。

另一方面，带有网络参数θG的损失函数由下式给出:

生成器的损失包括加权L1正则化项，确保产生的信号类似于参考输出信号y，这使得训练更加稳定。在等式2中，λ是一个超参数，我们将其固定为100，以便将损失函数的两个项缩放到可比较的幅度，从而防止正则化项主导优化问题。发生器损失的第一项促使生成器产生被鉴别器分类为1(即真实)的合成样本，这与鉴别器的损失函数相反。因此，生成器和鉴别器在训练期间的竞争利益驱使鉴别器产生越来越多的真实样本。

 3 GAN training

为了训练我们的模型，我们使用了癫痫项目数据库(Ihle等人，2012年)的数据，这是世界上最大的癫痫检测公共数据库之一。该数据集包含来自30名不同癫痫患者的记录，这些患者总共有277次癫痫发作，总计持续时间为21，001秒。EEG数据以256 Hz的采样频率收集，并被分成一个小时的记录，每个记录对应于一个记录时段。

在这项工作中，我们的目标是设置真实世界和无污点的可穿戴式监控设备(Hoppe等人，2015年)，因此我们只考虑标准10–20系统中的电极F7T3和F8 T4(Klem等人，1999年)，它们可以很容易地隐藏在眼镜中。我们提取持续时间为4秒的样本，因为这一长度对于检测癫痫发作是有效的。假设数据以256 Hz的频率记录，这导致长度为2048的样本，即每个电极1024个样本。为了构建训练集，我们将每个发作样本与来自同一患者的发作间样本配对。以这种方式，对于任何给定的患者，生成器学习将发作间样本映射到发作样本。为了训练GAN，遵循留一策略:对于每个目标患者，使用来自所有其他患者的发作和发作间数据来训练GAN。训练样本的确切数量取决于数据库中除了被遗漏的患者之外的所有患者的可用癫痫发作记录的秒数，并且尽管其略有变化，但其大约为20，000个样本。按照这个方案，对每个患者独立地训练GAN，因此，我们为每个患者获得一个模型。

4 Evaluation of Synthetic Data合成数据的评估

对于每个经过训练的模型，我们从来自训练期间被遗漏的患者的发作间期EEG信号中生成2000到6000个发作样本。在图1中，一些产生的样本显示在时域中。众所周知的δ-θ节律的存在，即振荡频率为0.5-4或4-7赫兹的节律性缓慢活动，清楚地表明了合成生成的EEG信号中的发作放电和癫痫发作段的正确生成(Osorio等人，2016)。

 图1:电极T3F7和T4F8的真实和合成发作样本的比较。可以看出在这两种情况下δ-θ节律是如何出现在信号中的。

为了评估生成的发作样本的质量，我们使用它们来训练基于随机森林算法的最先进的分类器(Díaz-Uriarte和De Andres，2006)。分类器的任务是确定输入的四秒样本是发作期样本还是发作间样本。在这里，我们遵循索皮奇等人(2018年)进行的实验，这些实验是为癫痫监测量身定制的无污名可穿戴设备。

我们独立地以每个患者为目标，并考虑用于训练癫痫检测算法的唯一可用数据是来自目标患者的真实发作间期样本和合成发作样本的情况。作为比较的基线，我们考虑来自所有其他患者的真实发作样本和来自目标患者的发作间期样本可用的情况。因此，我们首先建立一个目标和基线训练集。目标训练集包括来自目标患者的2000个合成发作样本和2000个真实发作间样本。从除目标患者之外的所有患者中随机选择的真实癫痫发作2000个样本的基线训练集和来自目标患者的2000个发作间期样本。这样，合成发作样本严格地说是目标训练集和基线训练集之间唯一不同的方面。然后，对于每个患者，我们为发作检测任务构建测试集，该测试集包含目标患者的所有发作样本，没有重叠，并且包含两倍数量的发作间样本。在训练GAN(目标患者被排除在外)的过程中没有使用这些测试发作样本，以确保没有信息泄漏。我们用两倍于发作样本的发作间样本来构建不平衡测试集，以便更好地再现真实世界的设置，其中发作样本在推断阶段中代表性不足。

一旦数据被分成训练集和测试集，就按照索皮奇等人(2018)的方法对数据执行特征提取步骤，并提取每个电极的功率和非线性的54个特征。然后，这两个训练集被用于在测试集上训练和评估随机森林分类器。为了稳健起见，我们将这些实验重复15次，每次都将数据拆分并混洗。

5 Results结果

为了评估我们实验中训练集的性能，我们使用敏感性和特异性的几何平均值(Fleming和Wallace，1986)。我们在附录a中报告了每位患者的这些实验的详细结果。

我们的结果表明，使用合成样本进行训练不仅不会降低性能，而且与仅使用通用数据库中的真实样本进行训练相比，总体性能提高了1.2%。除此之外，如图2所示，29名患者中的20名(即69%)改善超过1%，而29名患者中只有4名患者的性能下降超过1%。使用合成数据时性能改善的一个解释是，由于我们的GAN在给定来自同一患者的发作间期样本的情况下生成发作样本，因此该模型生成了保留许多个人特征的合成癫痫发作。这些结果证明了我们生成的合成发作数据的高质量，以及其对于癫痫检测的真实世界任务的实用性。

图2:模拟训练集和真实训练集在分类任务中的性能差异。纵轴代表患者数量，越大越好。

6 Conclusion结论

在这项工作中，我们提出了一个GAN模型，产生癫痫发作的合成脑电信号。据我们所知，在医疗领域，我们首次生成了可以训练检测算法的合成数据集，其结果可与真实数据的训练结果相媲美。我们的结果强调，在最常见的情况下，没有新患者癫痫发作的记录可用，训练可以完全使用合成发作。因此，使用现有的数据库，深度生成模型可以生成数据来训练系统监控新患者。我们的工作强调了深度生成模型(如GANs)在医学中的应用，可以帮助解决该领域的一些公开挑战，并有助于弥合对患有慢性疾病的患者采用连续监测系统的差距。对不成对的和有条件的深度生成模型的进一步研究可以提高合成训练集的质量和性能，从而允许基于合成数据的个性化医疗。

A Results

表1包含我们实验的每个患者的结果。患者22对于基线和合成训练集的表现都非常差，因此，它不是分类质量的相关指标。因此，它已从性能总差异的计算中移除。该总差异计算为合成病例中所有患者的几何平均值与基线病例中所有患者的几何平均值之间的差异。当患者22已经被排除时，这些结果通过了具有0.0098的p值的Wilcoxon统计显著性检验，这表明基线和合成训练集获得的结果之间的差异在统计上是显著的。

 表1:我们评估每个患者的敏感性和特异性的几何平均值

关于表现退化最显著的患者，即患者2和21，他们的癫痫发作由重复尖峰主导。这种模式相对罕见，在数据集中没有得到很好的体现(仅占癫痫发作的10.5%)。因此，我们的GAN模型不能像捕捉其他模式(如θ或δ节律)那样精确地捕捉这种行为。

事实上，患者22也患有具有重复尖峰的癫痫发作，并且我们的实验表明，即使最先进的技术也无法检测到这种癫痫发作。最后，患者20在该数据集中只有4次癫痫发作，这是整个数据集中癫痫发作次数最少的，并且妨碍了我们模型的稳健评估。

B GAN architectural details 构建细节

我们的GAN架构模仿SEGAN(Pascual等人，2017年)。我们的生成器是一个U-net (Ronneberger等人，2015年)卷积自动编码器，在除输入和潜在代码层之外的所有层中具有加权跳跃连接。跳跃连接的权重在训练期间学习。生成器的输入是长度为2048点的样本(以256 Hz的频率记录来自2个电极的4秒信号)。编码器由八个模块组成，这些模块交替使用卷积层和最大池层，最大池层具有2x2滤波器和步长为2。在编码器的每个块处提取的特征映射产生以下形状:2048×1、1024×64、512×64、256×128、128×128、64×256、32×256、16×512、8×1024；其中2048x1是输入的形状，8x1024是潜在编码的形状。平均值为0、标准偏差为1、形状为8×1024的高斯噪声被连接到潜在代码，以便将随机性引入模型。解码器与编码器对称，但它使用去卷积和膨胀。因此，解码器处的特征映射的形状是16×1024、16×512、32×256、64×256、128×128、256×128、512×64、1024×64、2048×1；其中2048x1是生成器的最终输出。跳跃连接将在编码器的每一层输出的特征图与学习的权重相乘，并在解码器处将其添加到相同形状的特征图。使用的激活是leakyReLu函数(Maas等人，2013年)，但解码器的最后一个模块除外，这里我们使用tanh函数。所有卷积和解卷积都是无偏的，并且在每个块之前应用频谱归一化(Miyato等人，2018年)。

鉴别器的架构与生成器的编码器具有相同的形状，但它在输出端包括一个额外的全连接层。通过这种方式，鉴别器输出1和0之间的单个值，其中1表示真实类，0表示合成类。最重要的是，在鉴别器中，我们应用了虚拟批量归一化(Salimans等人，2016年)以及光谱归一化。

为了训练模型，我们使用Adam (Kingma和Ba，2014)优化器，β1和β2的值分别为0和0.9，生成器的学习率为0.0001，鉴别器的学习率为0.0004。训练过程中使用的小批量数据的大小是100个样本。表2总结了所有使用的超参数。

C Evaluation details评估详情

在特征提取阶段，我们遵循索皮奇等人(2018)的方法，提取每个电极的功率和非线性的54个特征，即总共108个特征。为了计算非线性特征，使用离散小波变换将信号分解到第七级。提取的非线性特征是:k = 0.2和k = 0.35的第六和第七级样本熵(Richman和Moorman，2000)；n = 3、n = 5和n = 7的第三、第四、第五、第六和第七级排列熵(Bandt和Pompe，2002年)；第三、第四、第五、第六和第七级，以及原始信号、香农、雷尼和察利斯熵。功率特征是:总功率、频带δ[0.5，4] Hz、θ[4，8] Hz、α[8，12] Hz、β[13，30] Hz、γ[30，45] Hz以及频带[0，0.1] Hz、[0.1，0.5] Hz、[12，13] Hz中的总的和相对的频带功率。