计算机视觉（三）图像拼接

一、流程与概念

1.1 流程

要拼接多张图像，就一定要找到他们之间的映射关系，流程如下：

得到映射关系，就能进行拼接：

简而言之，拼接两张图像，就是找到他们的特征点，根据这些特征点：

1.2 映射与处理

找到两张图像的像素点对应关系，然后把第二张图像映射到在第一张图像的坐标系下，二者合成新的图像，若是有多张图，就重复这个步骤。
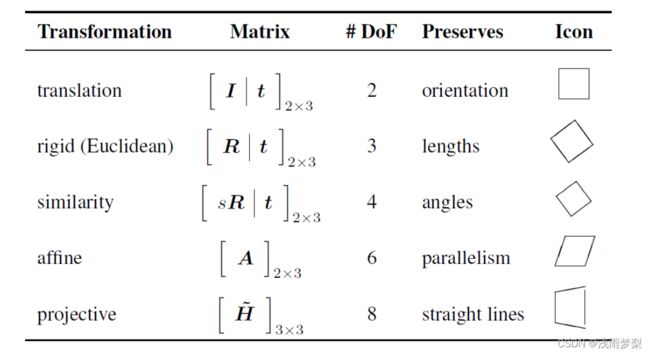
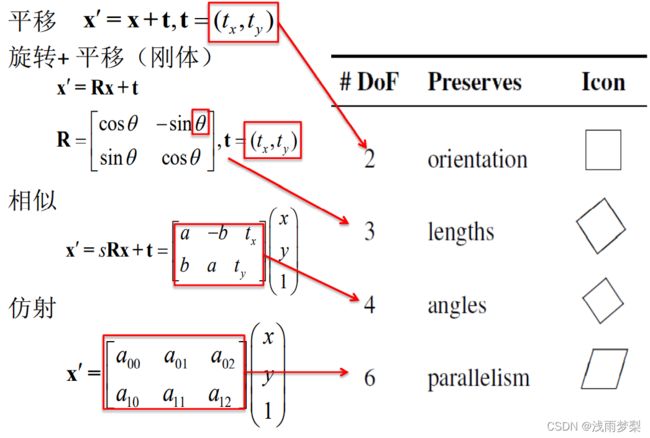
下面给出了不同映射需要的特征点数：

二、算法

2.1 全景拼接

将SIFT应用到图像拼接上，根据特征点匹配的方式，则利用这些匹配的点来估算单应矩阵使用RANSAC算法，也就是把其中一张通过个关联性和另一张匹配的方法。通过单应矩阵H，可以将原图像中任意像素点坐标转换为新坐标点，转换后的图像即为适合拼接的结果图像。
可以简单分为以下几步:
1.根据给定图像/集，实现特征匹配。
2.通过匹配特征计算图像之间的变换结构。
3.利用图像变换结构，实现图像映射。
4.针对叠加后的图像，采用APAP之类的算法，对齐特征点。(图像配准)
5.通过图割方法，自动选取拼接缝。
6.根据multi-band blending策略实现融合。

2.2 RANSAC算法

在找特征点时，不可避免的会出现噪声，因此要找到一种算法，让多张图像的特征点能够正确的进行映射。
用RANSAC 算法求解求解单应矩阵。
RANSAC[1] (随机抽样一致)是一种迭代算法，该算法从一组包含“外点(outlier)”的观测数据中估计数学模型的参数。“外点”指观测数据中的无效数据，通常为噪声或错误数据，比如图像匹配中的误匹配点和曲线拟合中的离群点。与“外点”相对应的是“内点(inlier)”，即用来估计模型参数的有效数据。因此，RANSAC也是一种“外点”检测算法。此外，RANSAC算法是一种非确定算法，它只能在一定概率下产生可信的结果，当迭代次数增加时，准确的概率也会增加。

RANSAC算法是用来找到正确模型来拟合带有噪声数据的迭代方法。
基本思想：数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摈弃噪声点。
流程如下：

2.3 APAP算法

在图像拼接融合的过程中，受客观因素的影响，拼接融合后的图像可能会存在“鬼影现象”以及图像间过度不连续等问题。下图就是图像拼接的一种“鬼影现象”。解决鬼影现象可以采用APAP算法。
算法流程：

1.提取两张图片的sift特征点
2.对两张图片的特征点进行匹配
3.匹配后，使用RANSAC算法进行特征点对的筛选，排除错误点。筛选后的特征点基本能够一一对应
4.使用DLT算法，将剩下的特征点对进行透视变换矩阵的估计
5.由于得到的透视变换矩阵是基于全局特征点对进行的，即一个刚性的单应性矩阵完成配准。为提高配准的精度，Apap将图像切割成无数多个小方块，对每个小方块进行单应性矩阵变换，非常依赖于特征点对。若图像高频信息较少，特征点对过少，配准将完全失效，并且对大尺度的图像进行配准，其效果也不是很好，一切都决定于特征点对的数量。

2.4 图像重合区处理

拼接两张图像，重叠部分的像素值取决于谁，是有说法的。
如图，用一种方式，在这部分区域划出一条路线，左边用A图，右边用B图

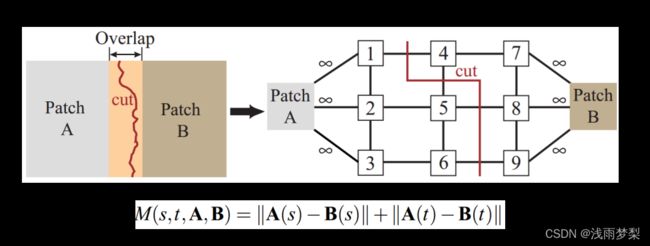
最大流
给定指定的一个有向图，其中有两个特殊的点源S(Sources)和汇T(Sinks)，每条边有指定的容量(Capacity)，求满足条件的从S到T的最大流(MaxFlow)。
最小割
割是网络中定点的一个划分，它把网络中的所有顶点划分成两个顶点集合S和T，其中源点s∈S,汇点t∈T。记为CUT(S,T)，满足条件的从S到T的最小割（Min cut）。
最大流的值等于最小割的容量。
给出福特福克森算法如下：

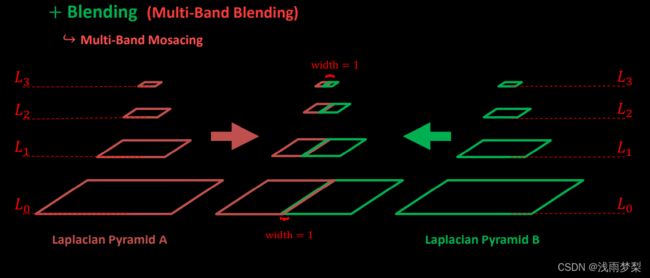
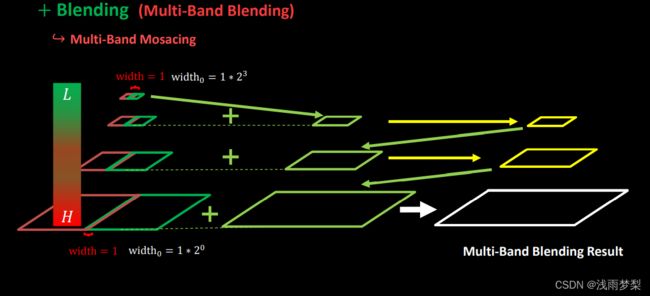
2.5 multi-band blending算法

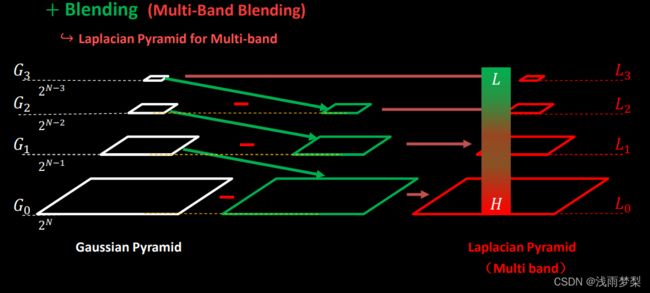
在找完拼接缝后，由于图像噪声、光照、曝光度、模型匹配误差等因素，直接进行图像合成会在图像重叠区域的拼接处出现比较明显的边痕迹。这些边痕迹需要使用图像融合算法来消除。而multi-band blending是目前图像融和方面比较好的方法。
multi-band bleing策略采用Laplacian（拉普拉斯）金字塔，通过对相邻两层的高斯金字塔进行差分，将原图分解成不同尺度的子图，对每一个之图进行加权平均，得到每一层的融合结果，最后进行金字塔的反向重建，得到最终融合效果过程，融合之后可以得到较好的拼接效果。

三、实现与运行

3.1 代码实现

# -*- codeing =utf-8 -*-

from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift

np.seterr(invalid='ignore')
"""
This is the panorama example from section 3.3.
"""

# 设置数据文件夹的路径
featname = ['E:/CV/img/img' + str(i) + '.sift' for i in range(4)]
imname = ['E:/CV/img/img' + str(i) + '.jpg' for i in range(4)]

# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(4):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(3):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化匹配
for i in range(3):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

# tp, fp = convert_points(3)  # NB: reverse order
# H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3

# 扭曲图像
delta = 2000  # for padding and translation用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

# im1 = array(Image.open(imname[4]), "f")
# im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)

figure()
imshow(array(im_32, "uint8"))
axis('off')
show()

3.2 结果

原图与运行结果如下：