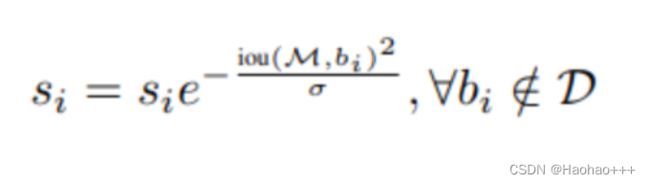NMS与Soft NMS算法解析以及numpy实现

1. NMS算法

1.1 什么是NMS算法

NMS全称为Non Maximum Suppression，中文意思是非极大值抑制，字面意思就是不是极大值的元素被抑制掉，其实就是筛选出局部最大值得到最优解。NMS算法被广泛运用于目标检测算法处理网络输出的边界框。

1.2 为什么在目标检测中要使用NMS算法

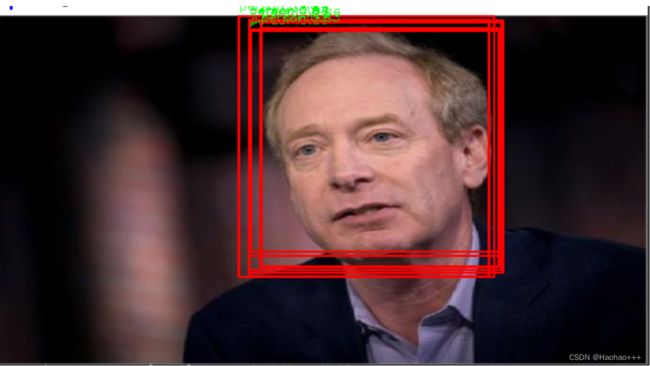
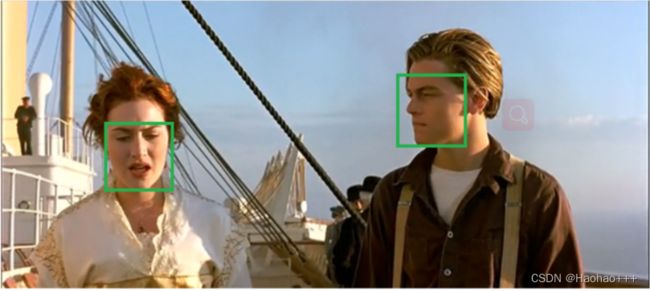
在目标检测中如果不是用NMS算法，则网络的输出结果就会向如下图所示，许多预测框都框住了目标，但是这些框并不是我们都想要的，我们想要的是其中框出来最好的那一个预测框。此时，我们就需要利用NMS算法去筛选出最适合的预测框。

1.3 在目标检测中怎么样使用NMS算法

我们以检测人脸为例，在目标检测中使用NMS算法的流程：

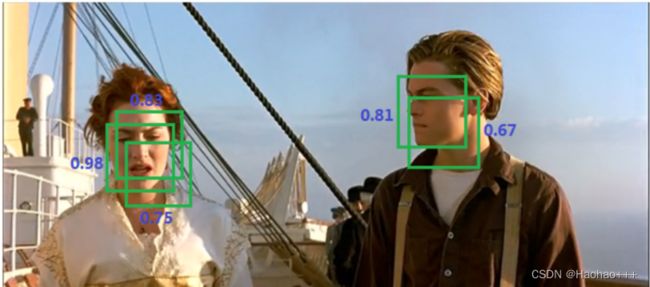
1. 首先，需要通过置信度阈值消除小于阈值的预测框，比如阈值为0.5，如图下图所示，得到过滤后的预测框。

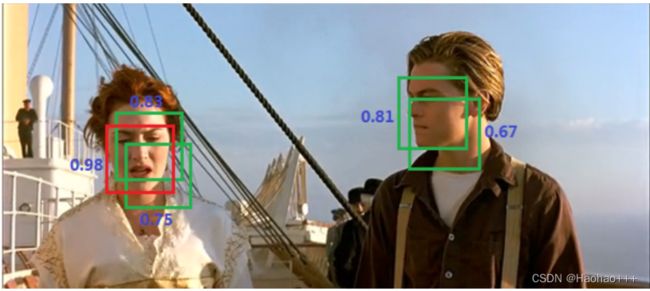
2. 将所有的预测框的置信度降序排列，得到置信度最大的预测框，如下图红色框：

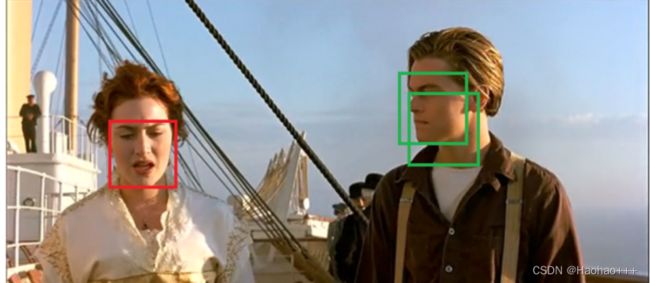
3. 再设置一个IOU阈值，所谓IOU就是两个框面积的交并比，遍历其余的框，如果和当前最高分框的IOU大于一定阈值，我们就将框删除，如下图所示。

4. 再重复1、2、3步骤，得到最终的结果。

Python代码如下：
代码来自：https://github.com/rbgirshick/fast-rcnn/blob/master/lib/utils/nms.py

import numpy as np

def nms(dets, thresh):
	# ------------------------------------ #
	# 获取所有预测框的左上角x1, y1、右上角x2, y2以及置信度scores
	# ------------------------------------ #
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]
	# ------------------------------------ #
	# 获取所有预测框的面积
	# ------------------------------------ #
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    # ------------------------------------ #
	# 所有预测框降序排列（保存的是下标）
	# ------------------------------------ #
    order = scores.argsort()[::-1]
    
	# ------------------------------------ #
	# keep为最后计算保留下来预测框的下标
	# ------------------------------------ #
    keep = []
    while order.size > 0:
    	# ------------------------------------ #
    	# 取出置信度值最大的下标
    	# ------------------------------------ #
        i = order[0]
        keep.append(i)
        
        # ------------------------------------ #
    	# 计算IOU
    	# ------------------------------------ #
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[order[1:]] - inter)
		# ------------------------------------ #
    	# 过滤小于IOU阈值的边界框
    	# ------------------------------------ #
        inds = np.where(ovr <= thresh)[0]
        # ------------------------------------ #
        # ovr 数组的长度比 order 数组少一个，这里将所有下标后移一位
        # ------------------------------------ #
        order = order[inds + 1]

    return keep

2. Soft NMS算法

2.1 什么是Soft NMS算法

Soft NMS是对NMS的优化算法，它在不增加额外参数的情况下且只需要对NMS算法进行简单的改动就能提高AP。该Soft-NMS算法在标准数据集PASCAL VOC2007（较R-FCN和Faster-RCNN提升1.7%）和MS-COCO（较R-FCN提升1.3%，较Faster-RCNN提升1.1%）上均有提升。

Soft NMS的主要思想

如下图所示，假设重叠的阈值为 0.5，图 中当黑框与红框比较时，两者之间的IoU为0.51，则红框将被删除，即使置信度高于许多其他 IoU 较小的框。因此，如果有两个并排的对象，则其中一个将被消除，这会降低模型的精度。

NMS与Soft NMS都有一个共同点，都是从置信度最大的框开始逐渐迭代的。

因此，Soft NMS则不再是直接将大于重叠的阈值的框删除，而是根据重叠程度衰减框的置信度得分，再根据设定的置信度阈值，去除小于置信度阈值的框。

改变置信度的方法有两种：

1. 线性法

如下公式：
其中，$iou(M,b_i)$代表最大置信度得分的框$M$与第$i$个框$b_i$的IOU，$N_t$代表重叠的阈值，$s_i$代表第$i$个框的置信度得分$s_i$

通过分析可以得出，当重叠的IOU增大时，置信度得分确实得到线性的下降。

2. 高斯法

如下公式：
其中：$iou(M,b_i)$代表最大置信度得分的框$M$与第$i$个框$b_i$的IOU，$\sigma$为一个可设定的常数，$s_i$代表第$i$个框的置信度得分$s_i$。

通过分析可以得出，当重叠的IOU增大时，置信度得分确实下降了。

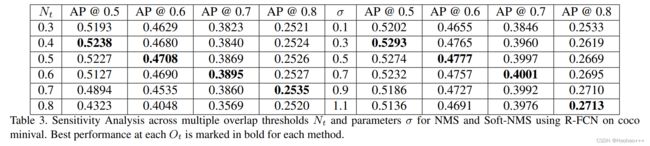
如下图是原论文中Soft NMS在R-FCN中$N_t$与$\sigma$的变化对AP的影响。

2.2 代码实现：

参考代码：https://github.com/DocF/Soft-NMS/blob/master/soft_nms.py

import numpy as np



def py_cpu_softnms(dets, sc, Nt=0.3, sigma=0.5, thresh=0.001, method=2):
    """
    py_cpu_softnms
    :param dets:   boexs 坐标矩阵 format [y1, x1, y2, x2]
    :param sc:     每个 boxes 对应的分数
    :param Nt:     iou 交叠门限
    :param sigma:  使用 gaussian 函数的方差，根据需要设置
    :param thresh: 最后的分数门限
    :param method: 使用的方法
    :return:       留下的 boxes 的 index
    """

    # indexes concatenate boxes with the last column
    N = dets.shape[0]
    indexes = np.array([np.arange(N)])
    dets = np.concatenate((dets, indexes.T), axis=1)

    # the order of boxes coordinate is [y1,x1,y2,x2]
    y1 = dets[:, 0]
    x1 = dets[:, 1]
    y2 = dets[:, 2]
    x2 = dets[:, 3]
    scores = sc
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    for i in range(N):
        # intermediate parameters for later parameters exchange
        tBD = dets[i, :].copy()
        tscore = scores[i].copy()
        tarea = areas[i].copy()
        pos = i + 1

        #
        if i != N-1:
            maxscore = np.max(scores[pos:], axis=0)
            maxpos = np.argmax(scores[pos:], axis=0)
        else:
            maxscore = scores[-1]
            maxpos = 0
        if tscore < maxscore:
            dets[i, :] = dets[maxpos + i + 1, :]
            dets[maxpos + i + 1, :] = tBD
            tBD = dets[i, :]

            scores[i] = scores[maxpos + i + 1]
            scores[maxpos + i + 1] = tscore
            tscore = scores[i]

            areas[i] = areas[maxpos + i + 1]
            areas[maxpos + i + 1] = tarea
            tarea = areas[i]

        # IoU calculate
        xx1 = np.maximum(dets[i, 1], dets[pos:, 1])
        yy1 = np.maximum(dets[i, 0], dets[pos:, 0])
        xx2 = np.minimum(dets[i, 3], dets[pos:, 3])
        yy2 = np.minimum(dets[i, 2], dets[pos:, 2])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[pos:] - inter)

        # Three methods: 1.linear 2.gaussian 3.original NMS
        if method == 1:  # linear
            weight = np.ones(ovr.shape)
            weight[ovr > Nt] = weight[ovr > Nt] - ovr[ovr > Nt]
        elif method == 2:  # gaussian
            weight = np.exp(-(ovr * ovr) / sigma)
        else:  # original NMS
            weight = np.ones(ovr.shape)
            weight[ovr > Nt] = 0

        scores[pos:] = weight * scores[pos:]

    # select the boxes and keep the corresponding indexes
    inds = dets[:, 4][scores > thresh]
    keep = inds.astype(int)

    return keep