初探强化学习(7)基于模型的强化学习的应用综述
本文是直接翻译一篇文章的,我先把原文地址放在这里。
原文名字为:Survey of Model-Based Reinforcement Learning: Applications on Robotics
这是一个2017年的论文
1. Introduction
强化学习(Regulation Learning,RL)是人工智能领域的一个重要方面,有着从金融到机器人等众多应用,并提出了大量的方法。机器人技术对于RL来说是一个非常具有挑战性的应用,因为它涉及机械系统与其环境之间的交互。这种相互作用会对机械系统和人类造成伤害,尤其是在服务和工业机器人中,这些机器人预计会在接近人类的地方工作。另一方面,RL可以提高机器人系统的适应性,这是处理复杂动态环境的一个重要特征。自然地,在过去几年里,RL在机器人控制领域的应用越来越广泛[1,2]。考虑到未来几年机器人将变得比仅仅能够重复一组明确的简单动作更智能,这一事实就不足为奇了。这项工作背后的动机是基于一项观察,即已经发表了大量关于机器人RL的调查论文[1-3],但它们都主要集中在无模型方法上。然而,近年来,基于模型的RL在机器人技术中的应用越来越受到关注[4-11]。这项调查的另一个推动因素是观察到机器人本身正在发生变化;低成本的协作机器人已经成为机器人市场的一个重要组成部分,并有望在未来几年获得更大的普及。这种机器人的成本较低,不可避免地会影响其准确性和可重复性,以及其内部传感设备的质量。因此,我们需要重新考虑应用于这种新型机器人的学习技术的特点。
这项工作的目标有两个:
- 提供机器人学RL的最新概述,重点介绍基于模型的方法,并展示其相对优势;
- 调查RL方法在应对低成本机械手挑战方面的适用性,并在第7节中总结出一种稳健可靠的基于模型的RL方法,用于使用低成本机械手执行任务。
为了实现第一个目标,我们研究了基于模型的RL在模拟和真实机器人系统上的应用文献。我们介绍了价值函数和策略搜索方法,以及设置返回函数(returns function)和学习过度模型(transition model)的策略,这些策略已成功应用于机器人系统。我们只有在分析了最新技术之后,并结合第一个目标产生的结果,才能实现第二个目标。
这项调查的组织如下。在这一介绍性章节之后,我们将在第2节介绍用于基于模型的RL的值函数方法。第3节讨论了返回函数,第4节讨论了策略搜索方法。此外,在第5节中,我们介绍了建模过渡动力学的方法。第6节回顾了基于模型的RL方法在机器人平台上用于学习各种任务的案例。最后,我们在第7节总结了这项调查的结果,并讨论了基于模型的RL在文献中已经报道的应用之外的应用中的适用性。
1.1 基于模型的强化学习背景
RL与其他类型的机器学习之间的主要区别在于,学习过程涉及agent与其环境之间的交互,因此agent通过直接从其环境中收集经验来学习所需的任务,而不需要外部教师。然而,这两个组件(agent和环境)之间的区别并不总是直接的,而是取决于应用程序。例如,在双足步行和无人机控制等应用中,假设环境包括机器人的电机。
机器人的状态可以用连续或离散的方式描述。在每种状态下,机器人控制器都会应用一个动作 a a a(电机指令),从而改变其状态。这些动作源自一个策略函数 π ( ⋅ ) π(·) π(⋅),在确定性的情况下,该函数将状态映射为一个动作 π ( s ) → a π(s)→a π(s)→a。在随机情况下,策略函数依赖于一个随机变量ε,映射被写成作用 π ( a ∣ s , ε ) π(a | s,ε) π(a∣s,ε)上的概率分布。
强化学习算法的目标是找到最大化预期收益的策略,该策略由奖励函数r定义。指示agent回报的主要函数类型可以是折扣函数或平均函数,并在有限或无限的范围内计算。当学习到的任务有一个已知的结束状态时,使用有限视界,否则更适合使用无限函数。
机器人与环境之间的交互被建模为马尔可夫决策过程(MDP)、元组 [ S , a , ε , P ( s ′ ∣ s , a ) , R ( s , s ′ , a ) , γ ] [S,a,ε,P(s'|s,a),R(s,s',a),γ] [S,a,ε,P(s′∣s,a),R(s,s′,a),γ]。其中,S是可能的机器人状态集,A是动作集, P ( s ′ ∣ s , a ) P(s' | s,a) P(s′∣s,a)是机器人处于状态S并应用动作A时在未来状态 s ′ s' s′的转移概率。 R ( s , s ′ , a ) R(s,s',a) R(s,s′,a)是机器人在转移到状态 s ′ s' s′时预期的奖励,取决于应用的动作 a a a,状态 s s s,并通过奖励函数计算。最后, γ γ γ是奖励函数的折扣因子。
RL方法分为两大类,无模型(也称为直接)和基于模型(也称为间接)的方法。基于模型和无模型的RL之间的主要区别在于是否采用了机器人与环境之间交互的模型。在无模型方法中,没有模型,因此奖励和最佳行动是通过物理系统的试错方法得出的。在基于模型的方法中,存在一个过渡动力学(transition dynamics)模型,用于推导奖励和最佳行动。因此,在模型中对策略进行优化,并在物理系统中应用最优策略。图1展示了一个基于模型的RL管道。

无模型方法吸引了更多的科学兴趣,但用于推导最优策略的采样轨迹在应用于实际机器人时可能是一个缺点。另一种方法是使用基于模型的方法。在这种情况下,最优策略是基于与机器人动力学表示相对应的学习正向模型的内部模拟推导出来的。该特性显著减少了机器人与其环境之间的物理交互,从而显著减少了机械磨损。另一方面,它的主要缺点是基于模型的RL算法严重依赖于模型准确表示过渡动力学(transition dynamics)的能力。表1总结了两类RL算法的优缺点。

RL问题的解可以从两个可选方法族中导出。最广泛使用的方法是价值函数方法,它估计处于给定状态并根据策略执行操作的agent的未来预期回报。在状态值函数 V π ( s ) = E π R t ∣ s t = s V^{π}(s)=E_{π}{R_{t} | s_{t}=s} Vπ(s)=EπRt∣st=s中区分了值函数,这是在遵循策略π的状态下的预期收益,以及动作值函数 Q π ( s , a ) = E π R t ∣ s t = s , a t = a Q^{π}(s,a)=E_{π}{Rt | s_{t}=s,a_{t}=a} Qπ(s,a)=EπRt∣st=s,at=a,这相当于在状态s中应用动作a并从那时起遵循策略π的未来预期收益。在有限学习范围H的情况下,返回函数是奖励 R t = ∑ t = 0 T r ( s t , a t ) R_{t} = {\textstyle \sum_{t=0}^{T}} r(s_{t},a_{t}) Rt=∑t=0Tr(st,at)的总和。在无限期的情况下,收益函数可以是折扣形式(12)或平均形式(13)。
Value function价值函数方法估计一个最优价值函数——状态值或动作值,以得出每个状态下的最优行动。因此,使长期回报最大化的策略是从每个状态的最佳动作中衍生出来的。价值函数方法分为四类:i)需要transition dynamics学模型的动态规划(DP)方法,ii)基于抽样的蒙特卡罗(MC)方法,iii)考虑两种状态transitions之间价值函数差异的时间差分学习(TDL)方法,以及iv)差分动态规划方法(DDP)。
值函数方法的替代方法是策略搜索方法。在策略搜索方法中,不是从最优值函数重构策略,而是直接学习最优策略。与价值函数方法相比,这一事实使得最先进的策略搜索方法在高自由度机器人系统的情况下能够更快地收敛[2,第2.3节]。策略由多种方法表示,从简单的线性函数到复杂的动态运动基元[1]。它们的共同特点是,它们都由一组参数进行参数化,必须对这些参数进行优化,以使累积报酬最大化。
策略搜索涉及的方法包括:i)基于梯度的方法,在奖励函数的梯度上使用爬山方法更新参数化集,ii)期望最大化(EM)方法,通过最大化奖励的对数似然概率推断参数,iii)利用熵等概念推导优化策略的信息论方法,iv)贝叶斯优化方法,v)进化计算。
图2总结了解决RL问题的主要方法。本次调查的剩余部分将遵循这种分类法,以探索该领域的最新技术。

2. 值函数方法
RL问题的状态值函数可以用递归形式写成,如等式(1)所示,因此,状态的值函数取决于可能的未来状态的即时回报及其由转移概率加权的折扣值函数。
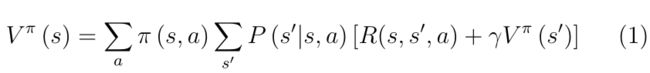
等效地,动作值函数可以以递归形式编写,如下所示:

方程(1)和(2)分别是状态值和动作值的贝尔曼方程( B e l l m a n − e q u a t i o n s Bellman -equations Bellman−equations )。价值函数方法的目标是计算价值函数,并通过最大化每个状态下的价值函数来得出最佳策略。可以证明存在一个最优策略 π ∗ π^{*} π∗,其值函数为最大值,最优状态值函数 V ∗ V^{*} V∗写成下式:
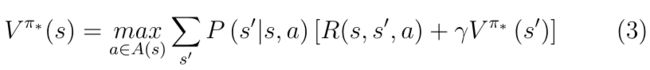
这对应于状态值函数的贝尔曼最优性方程。类似地,最优动作价值函数是一个贝尔曼最优方程,写为:
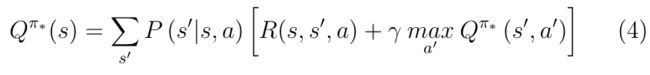
价值函数方法提供了推导最优价值函数的方法,用于重构最优策略。这类方法在基于模型的RL[9,10,12-26],[27-30]中非常流行,尤其是需要已知transition动力学模型的动态规划方法。其他方法,如蒙特卡罗法和时间差分法,主要用于无模型RL,因为它们不需要已知的模型。图3总结并分类了相关文献中的工作,其中价值函数方法已应用于基于模型的RL机器人系统。
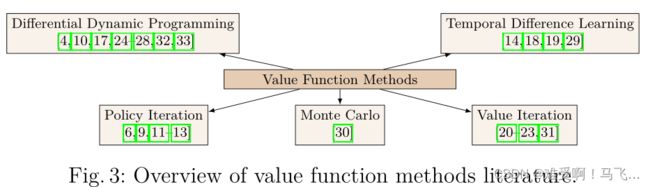
动态规划(DP)方法是迭代算法,可以分为策略迭代[34]和值迭代[35]。
策略迭代包括两个步骤;第一步是策略评估,为给定策略计算状态 s s s或动作 a a a值函数。这是从一个迭代过程中得出的,该过程计算每个状态的值函数,直到满足收敛标准。策略评估之后是策略改进步骤,在该步骤中,将导出每个状态的最佳操作。
2.1 策略迭代。
在[11,12]中,作者采用了一种策略迭代方法,使用自然参与者-批评家算法(Natural Actor-Critic algorithm)[36]。在Critic 部分,策略评估采用时间差分法,即LSTD-Q(λ)[37],而Actor部分采用自然梯度法进行策略改进[38]。[6]中还使用了一种参与者-批评家算法(actor-critic),作者在算法的critic部分使用值函数的梯度来改进策略推导。在[13]中,对LeastSquare策略迭代算法[39,40]的修改用于执行评估和改进步骤。在评估步骤中,使用动作值函数的参数近似,以减少状态空间。通过求解线性方程组来推导表征近似作用值函数的参数,改进了该策略。通过采用[41]中介绍的优先扫描(PS)技术,该算法的预测和时间效率得到了提高,该技术将状态值的更新集中在“感兴趣”的状态上。在[9]中,作者使用高斯过程[42]模型来近似动作值函数。
策略评估基于transition模型生成的样本,用于近似动作值。策略的改进可以通过贪婪方法来执行,该方法使用每个状态的最佳动作值,或者考虑每个状态的整个可能动作样本集。
2.2 价值迭代。
在策略迭代方法中,只有在评估步骤收敛后才更新策略,这可能是一项耗费时间和资源的任务。相比之下,值迭代方法不会等到评估过程收敛后才更新策略。在[20]中,值迭代法与PS结合使用。由于其并行执行,该算法针对在线学习进行了优化。[21]的作者使用了[43]中介绍的R-Max算法。它使用价值迭代来规划可重新定位的行动模型,这是一个分解的MDP[44]。RMAX是一种简单但功能强大的基于模型的RL算法,因为它可以在多项式计算复杂度下实现接近最优的性能[43]。该算法采用“不确定性下的乐观主义”方法,假设所有未知状态返回最大可能的回报,未知转换驱动到一个虚构的新状态。该算法由两个重复的步骤组成:计算和动作(act)以及观察和更新。在第一步中,agent基于其知识计算并应用最优策略,该策略将一直执行到事件结束或达到新状态。这一步之后是观察和更新步骤,在该步骤中,代理为每个采取的行动更新模型的奖励和转移概率,并重新计算最优策略。因此,R-MAX迫使智能体探索其领域,从而获得精确的模型和接近最优的策略。[45]中介绍了R-MAX算法的一个扩展,即关系资源管理器(REX),它可以处理关系状态空间[46],作者在[46]中对REX进行了扩展,以便它也可以处理专家的演示,避免危险的策略执行,并创建更安全的模型[47]。
在[22]中,作者提出了一种价值迭代算法RLDT,它通过执行有针对性的探索来减少与环境的交互。最后,在[23]中,作者还采用了价值迭代法来推导最优策略。
2.3 差分动态规划。
差分动态规划(DDP)是基于模型的RL中广泛使用的一种推导最优策略的方法。DDP算法起源于最优控制领域。它们执行局部轨迹优化,因此需要初始轨迹,以便采用两步优化程序。通过指定值函数的局部二次模型和与初始轨迹相对应的策略函数的线性模型来初始化DDP算法。在优化过程的第一步,将当前策略应用于动力学模型,生成模拟轨迹。在第二步中,生成的轨迹用于计算建模值函数在每个点的分量;然后相应地更新策略函数的参数。
[32]中采用了DDP,其中状态值函数的局部二次模型由值函数的一阶和二阶导数参数化,局部策略的模型取决于策略的梯度。在[17]中,作者介绍了Minimax DDP,其中使用了动作值函数的局部模型。除了传统的DDP,在Minimax DDP中,扰动的存在由状态值的局部模型中的扰动项表示。与传统的DDP相比,这种方法使得该算法能够处理更不准确的动力学模型。[33]中给出了DDP的随机扩展,其中状态由概率分布描述。与传统的DDP方法相比,它的进步在于,优化操作源自一阶梯度下降算法,且其收敛速度更快[48]。在[49]中,作者通过使用序列二次规划优化约束效用函数,实时执行轨迹优化。他们的方法允许实时规划轨迹,不需要计算或存储策略。
线性二次调节器(LQR)是DDP的一种特例,其中transition dynamics由线性近似建模,如方程(5)所示,由A和B参数化。其中A是m×m矩阵,B是m×k矩阵,m,k分别是状态 s s s和控制 a a a向量的维数。在LQR中,最优策略是状态和由(11)导出的矩阵 P i P_{i} Pi(6)的线性组合。在LQR的情况下,奖励函数表示处于状态 s s s并在时间步t应用动作 a a a的成本,它以二次形式表示,如(6)所示,参数Q和W分别是维数为m×m和k×k的正对称矩阵。

通过应用等式(5)和(6),必须优化的值函数可以写成:

可以通过以下值迭代过程进行优化。这就产生了每个i步的最优策略(等式(8))和最优状态值函数(等式(9))。

其中,矩阵K和P(10)和(11)使用DDP推导如下:
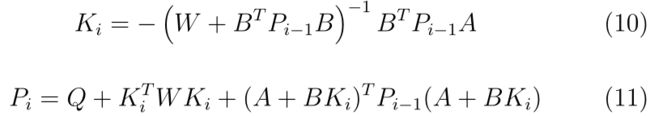
关于DDP和LQR的更详细介绍,请参见[50,51]和[52,第5章]。
在[28]中,作者使用LQR控制器,用少量数据学习所需的轨迹。此外,当与迭代学习控制方法结合使用时,LQR方法可以加快轨迹执行[10,24]。[27]的作者使用专家演示的轨迹,以进一步改进所学的最优策略。[4]中的作者采用了LQR的一种变体——迭代LQR,其目标是最小化最优轨迹和当前策略产生的轨迹之间的KL差异。最小化受到约束,确保算法收敛到匹配的优化轨迹和策略。LQR的一个缺点是假设线性确定性状态转换;这可以通过扩展来克服,例如高斯-牛顿LQR,这些扩展已被用于处理此类情况[25]。
其他方法。 DP的其他替代方法是时间差分(TD)和蒙特卡罗(MC)算法。尽管它们被认为是无模型方法,因为它们不需要transition dynamics的模型,但在transition dynamics未知的情况下,它们被用于基于模型的RL,而不是在线学习。MC算法是基于样本的,并使用生成的样本估计预期回报。TD学习算法基于其他估计以增量方式(自举)估计值函数,因此它们不需要完成RL任务。
在[30]中,作者使用蒙特卡罗树搜索算法来估计多线程体系结构中的动作值函数,以实现实时学习。[53]中介绍的SARSA的TD学习算法在[29]中使用。在那里,从状态转换中在线学习模型,然后用于估计动作值函数。在[14]中,作者使用了Dyna-Q算法,该算法将Qlearning[54]与Dyna框架[55]相结合,后者集成了模型学习、价值估计和代理的反应。[18,19]中还使用了Dyna-Q进行在线模型更新,以实现对所需任务的时间高效学习。
3. Return functions
选择合适的回报函数会对基于模型的RL算法的性能产生重大影响。返回函数影响学习任务的收敛性和可行性,因为最优策略的推导依赖于它。RL算法的目标是在每个时间步找到一组操作,从长远来看优化返回函数。返回函数汇总整个事件中的奖励或惩罚,即从初始状态s0到任务结束。
返回函数根据任务的长度进行分类,并将其累积为有限和无限水平函数。第一种方法更适用于目标状态已知的目标导向任务;因此,它们通常用于机器人应用。回报函数R之间的另一个区别是,每一步的奖惩R是否相等累积。折扣回报函数,如等式(12)所示
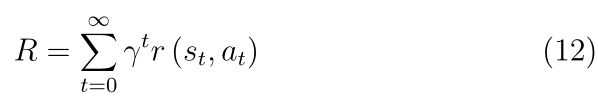
对早期奖励施加较大影响,其影响会随着时间的推移呈指数递减。另一方面,在平均回报函数中,如等式(13)所示
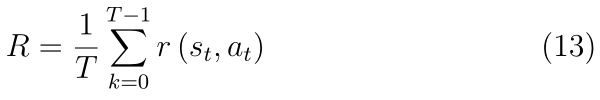
学习过程中获得的所有奖励都是等价累积的。图4根据这个标准组织了关于返回函数的相关文献。
折扣系数表示通过遵循策略获得的未来报酬的不确定性,由于不确定性随时间增加,未来报酬的影响减小。折扣系数 γ γ γ必须根据学习任务选择,并代表收敛时间和学习任务质量之间的折衷。因此,较小的折扣因子会导致RL算法的快速收敛。然而,由于在期限结束时获得的奖励对回报函数的影响非常小,因此学习到的解决方案的质量可能不令人满意。
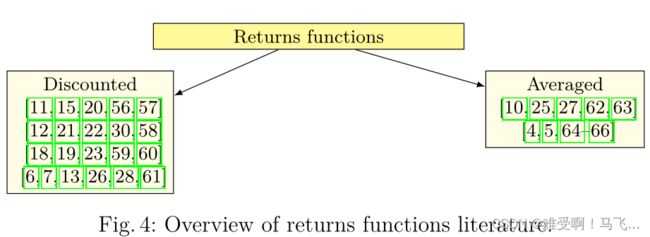
折扣回报函数是基于模型的RL机器人技术应用中最流行的。奖励函数的选择在很大程度上取决于学习任务的目标、机器人的约束以及策略优化过程的选择。在许多提出的方法[5,7,10–12,20,58,59,67]中,奖励是目标和当前状态之间的距离度量。在其他一些情况下,它是一个成本函数,用于惩罚偏离已证明轨迹的情况[6,16,24,25,27,56]。此外,当应用微分动态规划来推导最优策略时,reward必须近似为二次型[16,24]。在状态空间离散化的应用中,奖励的形式为阶跃函数[13,20,22]。还可以在奖励函数中引入机器人和环境的约束;例如作为惩罚冲突或接近冲突状态的成本组成部分[62]。最后,存在一些方法,可以对机器人采取的所有不将其推向目标状态的动作增加一点惩罚[18,23]。这恰好实现了学习算法的更快收敛。
4. 策略搜索方法
策略搜索方法是导出最优策略的另一种方法。价值函数方法通过寻找在每个状态下使价值函数最大化的动作(actions)间接构造策略,而策略搜索方法通过修改其参数直接计算最优策略。推导最优参数的算法可分为三大类和几个不太流行的类。基于梯度的方法试图通过采用梯度上升方法来优化参数化策略函数。它们的主要缺点是需要设置梯度步长参数,这会影响算法的收敛性。另一方面,sampling-based的方法不受此问题的影响。策略由使用迭代算法推断的潜在变量参数化。然而,它们的缺点是不能保证收敛到最优轨迹,并且它们可以创建远离所用过渡模型的训练数据的轨迹。另一方面,信息论方法通过限制轨迹探索来解决这些问题。最后,还采用了基于贝叶斯优化和进化计算的方法。策略搜索方法的分类如图5所示。

4.1 Gradient-based。
在[57]中,直接梯度算法[74]用于策略优化。该策略被参数化为一个人工神经网络,其权重在策略搜索过程中被修改。作者通过训练一个模拟最优策略并将其转移到实际系统进行进一步修改,加快了学习时间。在[59]中,作者使用梯度上升法来实现预期回报的最大化。[67]中介绍并在[5,62,63,68]中应用的学习控制概率推理(PILCO)框架是解决RL问题的最先进方法,因为它需要少量数据来学习策略,并且具有时间效率。该算法的关键特征是transition dynamics学模型处理其输入不确定性的能力[75]。这一特性使得对长轨迹视界的预测更加准确,因此减少了建模误差的影响。
PILCO采用梯度法进行策略改进。控制器的优化准则是长期预期收益的最小化,这会影响到与目标的距离。对于梯度的推导,作者利用偏导数链规则。
更详细地说,PILCO 使用高斯过程作为学习transition dynamics学的方法(进一步参见第 5 节),它为机器人在地平线(horizon)的每个时间步长的状态生成一组预测分布。 因此,关于机器人状态的预测是随机的,并由正态分布 ( p ( s 1 ) , p ( s 2 ) , . . . , p ( s k ) ∼ N ( s k ∣ u k , ∑ k ) (p(s_{1}),p(s_{2}),...,p(s_{k})\sim N(s_{k}|u_{k}, {\textstyle \sum_{k}^{}} ) (p(s1),p(s2),...,p(sk)∼N(sk∣uk,∑k)描述。下一步是计算每个阶段的预期回报,如等式(14)所示。 因此,轨迹的预期回报源自轨迹的每个状态 s k s_{k} sk 的回报函数 r (·)。 奖励由处于该状态 N ( s k ∣ u k , ∑ k ) N(s_{k}|u_{k}, {\textstyle \sum_{k}^{}}) N(sk∣uk,∑k)的概率加权,因为它源自算法的转换模型。
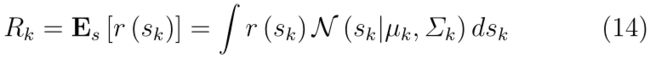
在这种情况下,奖励函数代表应用策略的一步成本,必须选择奖励函数以使等式 (14) 中的积分在分析上易于处理。
假设该策略是一个线性映射,并由一组参数 θ = [ A , b ] , π ( s k , θ ) \theta =[A,b],\pi (s_{k},\theta ) θ=[A,b],π(sk,θ)参数化,如等式(15)所示,目标是采用梯度下降法推导参数θ,使预期回报Rk最小化。

因此,通过应用链式法则,方程式(16)中的导数仍有待计算
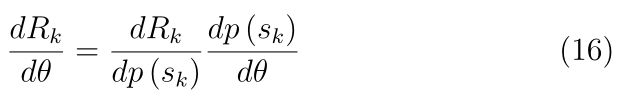
由于 p ( s k ) p(s_{k}) p(sk)是正态分布,它取决于两个参数,即正态分布的平均值 µ − k µ-k µ−k和协方差矩阵 ∑ k ∑_k ∑k。
因此,等式(16)可以写成:
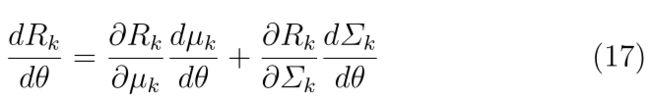
方程(17)中的导数可以通过迭代应用链式规则进行解析计算,这使得基于梯度的方法可以有效适用。有关其推导的更多详细信息,请参见[76]。
在 [63] 中,PILCO 被成功应用于结合降维学习高维系统的策略。 [68] 中的作者使用 PILCO 来推导模仿学习问题中的策略。 在这种情况下,目标函数基于 Kullback-Leibler (KL) 散度,这是对专家演示的轨迹与控制器创建的轨迹之间相似性的度量。 PILCO 在 [5] 中也被用于学习能够泛化到未知任务的策略。此外,[69] 中的作者采用了神经网络控制策略,其中网络的权重对应于学习的策略参数。 网络随机优化的目标是推导最符合最优轨迹的参数。 最佳轨迹是使用牛顿法最小化定义的成本函数的轨迹。
[70] 中提出了另一种基于梯度的策略优化方法,作者将基于参数的探索 (PGPE) 方法的无模型策略梯度扩展到基于模型的场景 (M-PGPE)。 在这种情况下,策略是确定性的,并表示为线性函数。因此,为了处理agent的探索,策略的参数是从依赖于一组超参数的概率分布中采样的。 该算法的目标是通过采用梯度上升法计算最大化预期收益的超参数。
4.2 Sampling-based
已应用于基于模型的 RL 上的策略搜索的基于采样的方法采用 [77] 中介绍的 PEGASUS(使用场景的策略评估和搜索)算法。 PEGASUS 通过将随机 MDP 或 POMDP 转换为近似确定性来处理抽样方差问题。 当随机模型用于转换动态时,模型的预测是下一个状态 p ( s t + 1 ) p(s_{t+1}) p(st+1) 的概率分布。因此,当使用随机模型评估固定策略时,下一个状态的预测会有所不同,因为它们是从概率分布中得出的。 因此,预期收益受到影响。 这个缺点在 PEGASUS 中通过使用一组固定的预定义随机数(稳定种子)增加(PO)MDP 来解决,这些随机数将随机转换为确定性转换模型。该算法通过近似确定性转移模型、奖励函数、随机数、描述初始状态的信念的分布和策略参数进行迭代和初始化。 目标是确定最大化奖励函数的策略参数。
PEGASUS 已在 [60] 中用于学习由四个可调参数组成的神经网络控制器。最大化奖励的策略参数来自爬山算法,该算法可以是梯度上升或随机游走。与从人类专家的演示中得出的策略相比,使用这种方法的学习策略的性能被发现更好。此外,[71] 中还提出了一种神经网络控制器。它的权重是根据 PEGASUS 算法调整的策略参数。在 [72] 中,作者应用 PEGASUS 来学习基于视觉系统输出的六个参数的控制器,该视觉系统能够识别来自单目相机的碰撞危险。在 [56] 中,PEGASUS 也用于学习具有 10 个自由参数的策略,并结合用于更新参数的 Nelder-Mead 方法。
4.3 Information Theory
信息论方法利用熵的概念作为优化策略参数的基础。在信息论领域,熵是对与事件相关的不确定性的度量。在基于模型的 RL 的上下文中,熵用于评估从策略生成的轨迹与参考轨迹相比——通常从外部演示者获得。[66] 中的作者介绍了变分引导策略搜索算法,用于为高维复杂任务推导合适的策略。该算法包括两个步骤,策略探索和策略优化步骤。第一步,差分动态规划用于轨迹探索,惩罚与当前策略的大偏差。在下一步中,策略的参数基于从探索步骤得出的轨迹进行优化。优化基于 KL 散度的最小化,这是一种熵度量,使用随机梯度下降执行。在 [65] 和 [8] 中,[78] 中介绍的无模型相对熵策略搜索(REPS)算法被扩展到基于模型的强化学习,用于学习可用于学习任务的广义上层策略 他们的上下文略有不同。上层策略和低层策略一起用于学习任务的泛化。因此,低级策略负责特定的上下文,例如在指定位置的运动,而上级策略概括了低级策略的这个特定上下文。高斯过程转换模型的使用通过生成用于更新策略的人工数据来减少训练所需的数据量。更好的是,它还减少了机器人与环境之间的相互作用。REPS 算法的目标是在不显着偏离观测数据的情况下优化广义策略。
此外,[61] 中提出了信任区域策略优化 (TRPO) 算法,其中目标函数根据 KL 散度约束进行优化。目标函数表示随机策略的预期回报,而 KL 散度对策略参数施加上限约束。 目标函数和散度约束均通过蒙特卡罗模拟逼近,优化问题通过共轭梯度法求解。
[79] 中引入了使用路径积分 (PI2) 算法的策略改进算法,该算法源自随机最优控制框架,并采用量子力学的路径积分概念来执行策略改进。 PI2 算法只有一个可调参数,即探索噪声,并且可以很好地扩展高维机器人学习问题,例如人形机器人的学习。与信息论方法的比较表明,后者可以作为随机最优控制的近似方法。此外,PI2可用于基于模型的[80,81]和无模型的RL方法[82],其中运动原语的概念[83]用于政策参数化。在Deisenroth等人[1]的调查中,可以找到PI2算法的扩展介绍。
[73]中提出了另一种基于路径积分的方法,即用于实现轨迹随机优化的模型预测路径积分控制(MPPI)。与标准的路径积分方法相反,MPPI不假设只有机器人通过其动作控制的状态才有噪声,还假设有噪声的间接控制状态。此外,该算法为整个学习范围内的最优控制提供了一个清晰的表达式。这些进步是通过利用相对熵的信息论概念实现的。因此,MPPI利用Radon-Nikodym导数和Girsanov定理的概念,使机器人的最优轨迹和跟随轨迹之间的熵最小化。
4.4 Other approaches
其他策略搜索方法包括贝叶斯优化[7]和进化计算[64]。在[7]中,贝叶斯优化用于减少对目标函数进行评估的次数,以获得最佳参数。这可以通过使用高斯过程模型对目标函数建模,并使用该模型评估目标函数来实现。另一方面,[64]中的作者采用进化计算方法,通过优化人工神经网络的权重来推导优化策略。
5. Transition Models
Transition Model T ( S , a , S ′ ) − − P r ( s ′ ∣ s , a ) T(S,a,S')--P_{r}(s'|s,a) T(S,a,S′)−−Pr(s′∣s,a): Transition Model, 根据当前状态 s s s 和动作 a a a 预测下一个状态 s ’ s’ s’,这里的 P r P_{r} Pr 表示从 s s s 采取行动 a a a 转移到 s ’ s’ s’ 的概率
Transition model是从机器人在horizon给定时间步的状态 s s s的映射 f ( s , a ) → s ′ f(s,a)→s' f(s,a)→s′,以及在下一个时间步应用的命令 a a a 到状态 s ′ s' s′。 由于策略学习步骤依赖于其预测的准确性,因此Transition model对基于模型的 RL 算法的性能有很大影响。我们将用于基于模型的强化学习的Transition model分为两大类——确定性模型和随机模型。确定性模型(Deterministic models)不依赖于随机变量来预测下一个状态,因此模型的预测对于给定的状态和动作将始终相同。另一方面,随机模型会产生由未来状态的概率分布定义的预测。 图 6 说明并分类了文献中用于基于模型的 RL 的模型。
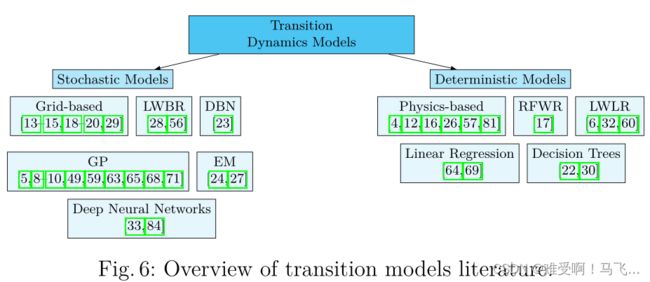
5.1 Deterministic Models确定性模型
描述transition dynamics的基于物理的模型被广泛用作确定性模型 [4, 12, 16, 26, 57, 81]。这种模型的主要缺点是它们包含许多难以分析表达的因素,例如弹性接头的摩擦力和动力学。另一个缺点是这些模型没有考虑机器人环境的潜在变化。为了解决这些问题,[15, 64] 中的作者使用线性回归增强了过渡的物理模型,以推断难以计算的模型参数。[17] 中还采用了基于物理和学习模型的组合,其中使用感受野加权回归 (RFWR) 对物理模型和真实机器人之间的误差进行建模。 RFWR——在 [85] 中介绍——是一个局部非参数模型,它是增量更新的。它的预测基于触发定义输入和学习数据之间相似性的感受野。
另一种方法,局部加权线性回归 (LWLR),已被应用于直接从感官数据中学习transition model,而无需了解机器人的模型 [6,32,60]。LWLR 是在 [86] 中引入的,是一种非参数模型,可以在训练数据上本地拟合线性回归模型。模型回归系数的预测是使用普通最小二乘估计器进行的,由一个内核加权,该内核提供新输入和学习数据之间相似性的度量。因此,更接近输入的数据点对预测的影响更大。 在[69]中还提出了局部线性回归模型的在线更新,用于学习双足机器人的contact dynamics。
决策树也被使用,因为它们能够很好地概括学习模型 [22, 30]。它们构成了一种分而治之的方法,因为它们划分了学习的数据空间以便对输入进行预测。划分是根据 C4.5 算法 [87] 进行的,该算法使用信息增益的概念(信息论概念)划分训练数据,将数据拆分到不同的节点,直到每个节点尽可能“纯”。
5.2 Stochastic Models(随机模型)
学习transition models(尤其是随机模型)的最先进方法是高斯过程 (GP),应用于 [5, 8-10, 49, 59, 63, 65, 68, 71] . 通常,概率模型在随机变量上构建分布,而 GP 在函数上构建分布。因此,没有关于将当前状态和动作映射到未来状态的函数 f 的任何假设。这一事实使 GP 成为一种强大的学习方法。GP 由其均值和内核(协方差函数)定义。在大多数情况下,假设 GP 的平均值为零,并且内核的一个非常常见的选择是那些属于指数族的内核。存在多种设置内核参数(超参数)的方法,包括对超参数空间的贪婪搜索和基于边缘似然的方法,这些方法使用更广泛。
更详细地说,在transition models的上下文中,GP 的目标是推断生成噪声观测值 s’ 的函数 f。 假设高斯噪声: s ′ = f ( s , a ) + N ( 0 , δ 0 2 I ) s'=f(s,a)+N(0,\delta_{0}^{2}I) s′=f(s,a)+N(0,δ02I) 并且为简化表示 x = ( s , a = (s, a =(s,a)。引用Rasmussen在[88]中的话,高斯过程可以定义为“随机变量的集合,任意有限个随机变量具有(一致的)联合高斯分布。”给定由D个属性描述的N个训练样本和一组 N ∗ N^{*} N∗测试样本组成的数据集,GP f的平均值 µ ( x ) µ(x) µ(x)和协方差 ∑ ( x , x ∗ ) ∑(x,x^{*}) ∑(x,x∗)分别在方程(18)和(19)中给出。

在大多数应用中,GP的平均函数为零,重点是选择适当的协方差函数(也称为核函数)及其参数。核函数起着重要作用,因为GP的性能强烈依赖于它们。根据它们在输入空间中对translations的不变性,它们被分类为stationery or not stationery。最常用的核是平方指数,如等式(20)所示,它取决于两个参数;方差 σ 2 σ^2 σ2和长度标度 λ λ λ。后者控制算法从训练数据推断出的距离。
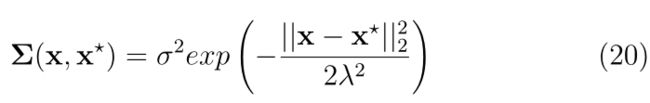
核参数的选择通常是通过优化给定训练数据的GP的对数似然来执行的,如方程(21)中的常数 β = − 1 2 l o g 2 π \beta =-\frac{1}{2} log2\pi β=−21log2π 。这个过程对应于负对数似然的关于协方差参数 θ θ θ的偏导数的最小化。因此,等式(22)的最小化,其中 a = ( ∑ ( x , x ) + σ n 2 ) s ′ a=(\sum (x,x)+\sigma _{n}^{2})s' a=(∑(x,x)+σn2)s′产生核的最佳参数,并且可以通过各种函数优化方法实现。

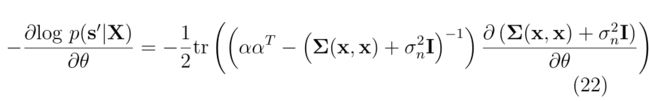
给定一个新的测试输入 x ∗ x^* x∗其预测目标值 s ∗ ′ s_{*}^{'} s∗′对应于等式(23)中给出的后验预测分布的平均值。另一方面,等式(24)中给出的协方差表示该预测的不确定性。

随机建模的一种常见方法,尤其是在基于模型的RL的早期,是将机器人的状态空间划分为网格,其中动作会根据概率分布在相邻网格上进行转换。在[13]中,transition models是基于从机器人与环境之间的相互作用中得出的经验估计值在线建立的。该模型基于对每个状态的访问频率、转换和即时奖励的统计。下一个状态的预测是通过求解线性方程组得出的。小脑模型关节控制器(CMAC)是一种基于网格的方法,在[15]中用于学习过渡模型。CMAC于[89]中引入,是一种基于重叠网格的值近似技术。新输入的预测基于每个网格的相关数据。在[29]中,状态聚合方法用于划分状态空间。网格对空间进行划分,根据训练数据的出现频率,每个动作都可以生成几个相邻的网格。[18,19]中的作者使用CACM算法[90]将状态空间离散化为单元。CACM基于相邻属性,确保仅在相邻小区之间进行转换。此外,在[14,20]中使用了查表方法。
[91]中介绍的局部加权贝叶斯回归(LWBR)在[28,56]中用作模型学习算法,它将贝叶斯推理和L WLR结合起来。回归系数给定高斯先验,噪声假设为伽马分布。每个输入的预测基于其与训练数据的相似性(由权重函数定义),并由t分布描述。
在[24]中,作者假设transition models由当前状态和应用命令与加性高斯噪声的线性组合来描述。线性方程的未知参数通过基于专家创建的参考轨迹的期望最大化(EM)算法进行优化。[27]中还使用了基于EM的方法,其中学习算法不仅可以预测未来的状态,还可以预测遵循由专家介绍的最佳轨迹所需的行动。EM算法的目标是推断出描述每个时间步的最佳状态和行为的潜在变量。另一种用于离散状态行动空间的方法是使用动态贝叶斯网络(DBN)[23]。在这种方法中,MDP转移概率的学习对应于DBN的局部结构的学习。多项逻辑回归的一种变体用于DBN的在线训练。
对于学习dynamics models,也提出了深度学习方法[33,84]。在[33]中,作者建议使用两种深度前馈网络架构,其中一种负责建模动力学,另一种负责建模误差和噪声。该网络的激活函数被选择为校正线性单元(ReLU),因为与常用的选择(如双曲正切)相比,它具有稳定性。这种方法的另一个优点是,网络可以处理其输入的不确定性,并且学习规则可以解析地导出。[84]中介绍了另一种学习工业机械手正向动力学的方法,即PC-ESN++,其中作者采用固定权重的递归神经网络作为隐藏层。输入与无监督学习规则无关,预测通过执行贝叶斯回归得出,噪声直接从数据中推断。该算法的优点是内存少,因此与其他方法相比计算效率更高。
[92]中提出了一种学习transition dynamics的密度估计方法,并将其应用于基于模型的RL[92,93]。最小二乘条件密度估计(LSCD)将转移概率建模为基函数和模型参数的线性组合。因此,该算法通过最小化平方差来学习这些参数。LSCD的优点是,与GP相比,它允许对转移概率进行更一般的假设。另一方面,它不具备数据效率,因为它需要大量数据来了解转换。在[93]中,作者通过执行监督降维方法来处理这个问题。
6. Applications on Robotics
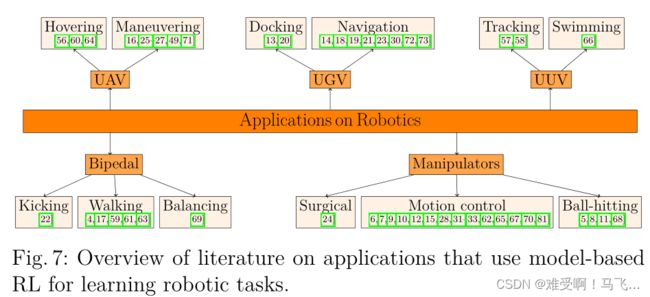
基于模型的强化学习已应用于从外科手术到水下机器人任务的各种机器人应用。图7组织了各种类型机器人系统的相关文献。
6.1 自动驾驶汽车
6.2 双足机器人
6.3 Robotic Manipulators。
另一个热门的应用领域是机器人的控制。任务领域从手术机器人到欠驱动机械手的运动控制[5-12,15,24,28,32,62,65,67,68]。作者在[24]中训练了两个伯克利手术机器人,以高速完成打结任务。此外,在一些应用中,作者训练机器人执行击球任务[5,8,11,68]。在[5,8]中,使用的平台是一个带有弹簧关节的兼容仿生机械手。状态空间是连续的,包含每个关节的位置和速度,而动作空间是三维的,包含施加的扭矩。在这两种情况下,机器人都接受过乒乓球相关任务的训练。此外,在[11]中,一个3自由度的机器人被训练来执行羽毛球摆动。学习执行机械手的运动控制已经应用于多种类型的平台,例如欠驱动机械手[7,15,28],低自由度机械手(2或3自由度)[6,7,9,10],以及更复杂的高自由度系统[12,32,67]。
学习的任务包括位置控制[6,7,10,15]、PR-2机器人浇注[33]、摆锤摆动[28,32]和更复杂的避障操作任务[12,62]。在大多数应用中,机械手的状态空间是连续的,由每个关节的位置和加速度来描述。作用空间也是连续的,对应于作用在驱动关节上的扭矩。图(10)给出了基于模型的RL在机械手上的应用分类。
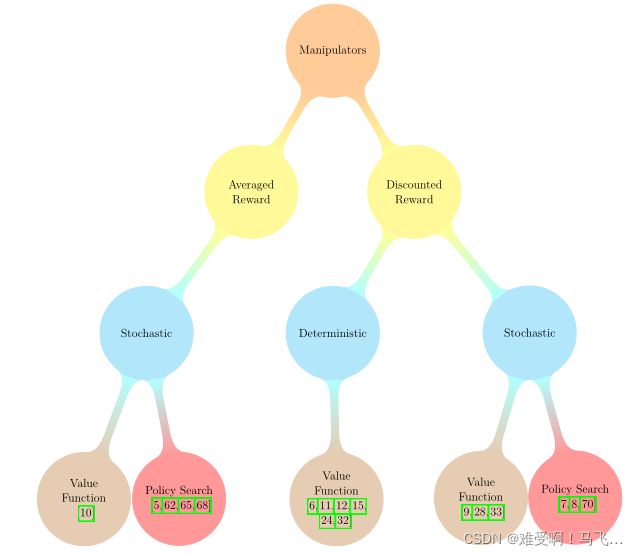
图 10:基于模型的 RL 应用在机器人机械手上的分类。每种提出的方法都根据所采用模块的类型进行分类。